vue diff 双端比较算法

news2024/9/25 13:24:16

文章目录

  • 双端指针
  • 比较策略
    • 命中策略四
    • 命中策略二
    • 命中策略三
    • 命中策略一
    • 未命中四种策略，遍历旧节点列表
    • 新增情况一
    • 新增情况二
  • 删除节点
  • 双端比较的优势

双端指针

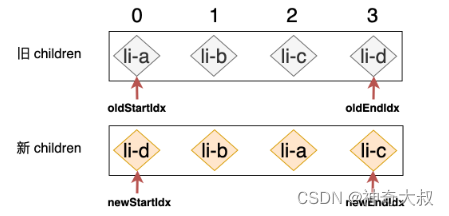
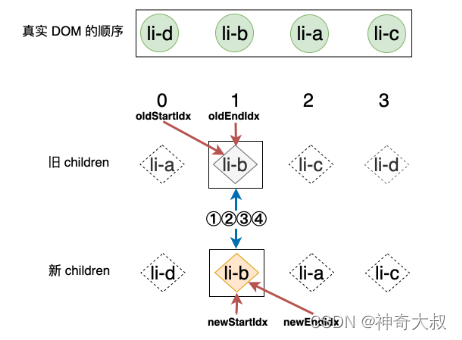
在这里插入图片描述

  • 使用四个变量 oldStartIdx、oldEndIdx、newStartIdx 以及 newEndIdx 分别存储旧 children 和新 children 的两个端点的位置索引
let oldStartIdx = 0
let oldEndIdx = prevChildren.length - 1
let newStartIdx = 0
let newEndIdx = nextChildren.length - 1
  • 除了位置索引之外，还需要拿到四个位置索引所指向的 VNode
let oldStartVNode = prevChildren[oldStartIdx]
let oldEndVNode = prevChildren[oldEndIdx]
let newStartVNode = nextChildren[newStartIdx]
let newEndVNode = nextChildren[newEndIdx]

比较策略

  • 使用旧 children 的头一个 VNode 与新 children 的头一个 VNode 比对，即 oldStartVNode 和 newStartVNode 比较对。
  • 使用旧 children 的最后一个 VNode 与新 children 的最后一个 VNode 比对，即 oldEndVNode 和 newEndVNode 比对。
  • 使用旧 children 的头一个 VNode 与新 children 的最后一个 VNode 比对，即 oldStartVNode 和 newEndVNode 比对。
  • 使用旧 children 的最后一个 VNode 与新 children 的头一个 VNode 比对，即 oldEndVNode 和 newStartVNode 比对。
    在这里插入图片描述
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  if (oldStartVNode.key === newStartVNode.key) {
    // 步骤一：oldStartVNode 和 newStartVNode 比对
  } else if (oldEndVNode.key === newEndVNode.key) {
    // 步骤二：oldEndVNode 和 newEndVNode 比对
  } else if (oldStartVNode.key === newEndVNode.key) {
    // 步骤三：oldStartVNode 和 newEndVNode 比对
  } else if (oldEndVNode.key === newStartVNode.key) {
    // 步骤四：oldEndVNode 和 newStartVNode 比对
  }
}

命中策略四

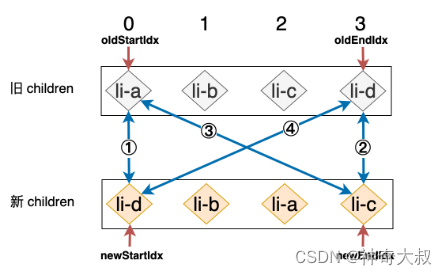
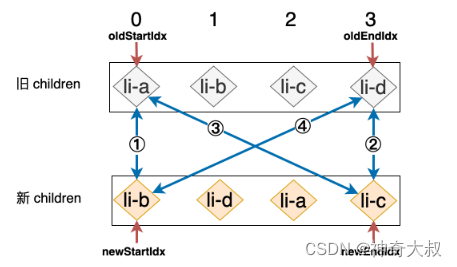
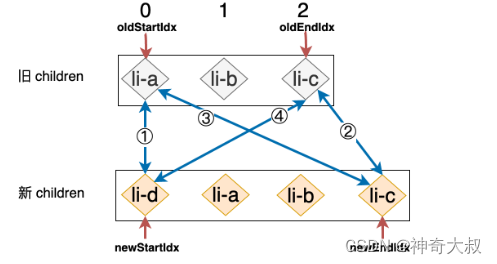
  • 第一步：拿旧 children 中的 li-a 和新 children 中的 li-d 进行比对，由于二者 key 值不同，所以不可复用，什么都不做。
  • 第二步：拿旧 children 中的 li-d 和新 children 中的 li-c 进行比对，同样不可复用，什么都不做。
  • 第三步：拿旧 children 中的 li-a 和新 children 中的 li-c 进行比对，什么都不做。
  • 第四步：拿旧 children 中的 li-d 和新 children 中的 li-d 进行比对，由于这两个节点拥有相同的 key 值，所以我们在这次比对的过程中找到了可复用的节点。
    • li-d 节点所对应的真实 DOM 原本是最后一个子节点，并且更新之后它应该变成第一个子节点。所以我们需要把 li-d 所对应的真实 DOM 移动到最前方即可：
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
	if (oldStartVNode.key === newStartVNode.key) {
	  // 步骤一：oldStartVNode 和 newStartVNode 比对
	} else if (oldEndVNode.key === newEndVNode.key) {
	  // 步骤二：oldEndVNode 和 newEndVNode 比对
	} else if (oldStartVNode.key === newEndVNode.key) {
	  // 步骤三：oldStartVNode 和 newEndVNode 比对
	} else if (oldEndVNode.key === newStartVNode.key) {
	  // 步骤四：oldEndVNode 和 newStartVNode 比对
	
	  // 先调用 patch 函数完成更新
	  patch(oldEndVNode, newStartVNode, container)
	  // 更新完成后，将容器中最后一个子节点移动到最前面，使其成为第一个子节点
	  container.insertBefore(oldEndVNode.el, oldStartVNode.el)
	  // 更新索引，指向下一个位置
	  oldEndVNode = prevChildren[--oldEndIdx]
	  newStartVNode = nextChildren[++newStartIdx]
	}
}

命中策略二

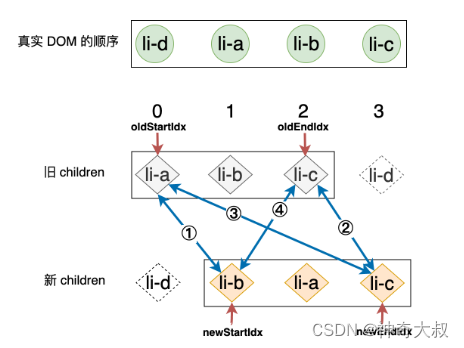
  • 上一步更新完成之后，新的索引关系可以用下图来表示：
    在这里插入图片描述
  • 第一步：拿旧 children 中的 li-a 和新 children 中的 li-b 进行比对，由于二者 key 值不同，所以不可复用，什么都不做。
  • 第二步：拿旧 children 中的 li-c 和新 children 中的 li-c 进行比对，此时，由于二者拥有相同的 key，所以是可复用的节点，但是由于二者在新旧 children 中都是最末尾的一个节点，所以是不需要进行移动操作的，只需要调用 patch 函数更新即可，同时将相应的索引前移一位
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  if (oldStartVNode.key === newStartVNode.key) {
    // 步骤一：oldStartVNode 和 newStartVNode 比对
  } else if (oldEndVNode.key === newEndVNode.key) {
    // 步骤二：oldEndVNode 和 newEndVNode 比对

    // 调用 patch 函数更新
    patch(oldEndVNode, newEndVNode, container)
    // 更新索引，指向下一个位置
    oldEndVNode = prevChildren[--oldEndIdx]
    newEndVNode = nextChildren[--newEndIdx]
  } else if (oldStartVNode.key === newEndVNode.key) {
    // 步骤三：oldStartVNode 和 newEndVNode 比对
  } else if (oldEndVNode.key === newStartVNode.key) {
    // 步骤四：oldEndVNode 和 newStartVNode 比对

    // 先调用 patch 函数完成更新
    patch(oldEndVNode, newStartVNode, container)
    // 更新完成后，将容器中最后一个子节点移动到最前面，使其成为第一个子节点
    container.insertBefore(oldEndVNode.el, oldStartVNode.el)
    // 更新索引，指向下一个位置
    oldEndVNode = prevChildren[--oldEndIdx]
    newStartVNode = nextChildren[++newStartIdx]
  }
}

命中策略三

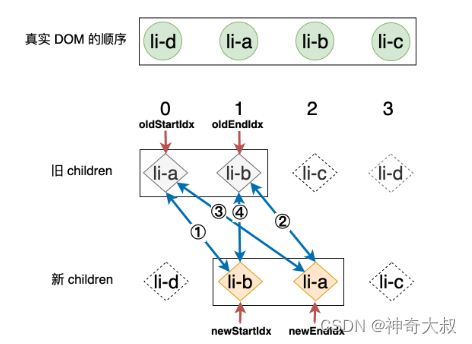
  • 上一步更新完成之后，新的索引关系可以用下图来表示：
    在这里插入图片描述
  • 第一步：拿旧 children 中的 li-a 和新 children 中的 li-b 进行比对，由于二者 key 值不同，所以不可复用，什么都不做。
  • 第二步：拿旧 children 中的 li-b 和新 children 中的 li-a 进行比对，不可复用，什么都不做。
  • 第三步：拿旧 children 中的 li-a 和新 children 中的 li-a 进行比对，此时，我们找到了可复用的节点。
    • 这一次满足的条件是：oldStartVNode.key === newEndVNode.key，这说明：li-a 节点所对应的真实 DOM 原本是第一个子节点，但现在变成了“最后”一个子节点，这里的“最后”并不是指真正意义上的最后一个节点，而是指当前索引范围内的最后一个节点。所以移动操作也是比较明显的，我们将 oldStartVNode 对应的真实 DOM 移动到 oldEndVNode 所对应真实 DOM 的后面即可
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  if (oldStartVNode.key === newStartVNode.key) {
    // 步骤一：oldStartVNode 和 newStartVNode 比对
  } else if (oldEndVNode.key === newEndVNode.key) {
    // 步骤二：oldEndVNode 和 newEndVNode 比对

    // 调用 patch 函数更新
    patch(oldEndVNode, newEndVNode, container)
    // 更新索引，指向下一个位置
    oldEndVNode = prevChildren[--oldEndIdx]
    newEndVNode = newEndVNode[--newEndIdx]
  } else if (oldStartVNode.key === newEndVNode.key) {
    // 步骤三：oldStartVNode 和 newEndVNode 比对

    // 调用 patch 函数更新
    patch(oldStartVNode, newEndVNode, container)
    // 将 oldStartVNode.el 移动到 oldEndVNode.el 的后面，也就是 oldEndVNode.el.nextSibling 的前面
    container.insertBefore(
      oldStartVNode.el,
      oldEndVNode.el.nextSibling
    )
    // 更新索引，指向下一个位置
    oldStartVNode = prevChildren[++oldStartIdx]
    newEndVNode = nextChildren[--newEndIdx]
  } else if (oldEndVNode.key === newStartVNode.key) {
    // 步骤四：oldEndVNode 和 newStartVNode 比对

    // 先调用 patch 函数完成更新
    patch(oldEndVNode, newStartVNode, container)
    // 更新完成后，将容器中最后一个子节点移动到最前面，使其成为第一个子节点
    container.insertBefore(oldEndVNode.el, oldStartVNode.el)
    // 更新索引，指向下一个位置
    oldEndVNode = prevChildren[--oldEndIdx]
    newStartVNode = nextChildren[++newStartIdx]
  }
}

命中策略一

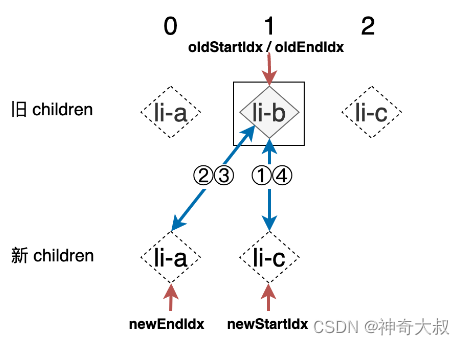
  • 上一步更新完成之后，新的索引关系可以用下图来表示：
    在这里插入图片描述
  • 第一步：拿旧 children 中的 li-b 和新 children 中的 li-b 进行比对，二者拥有相同的 key，可复用
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  if (oldStartVNode.key === newStartVNode.key) {
    // 步骤一：oldStartVNode 和 newStartVNode 比对

    // 调用 patch 函数更新
    patch(oldStartVNode, newStartVNode, container)
    // 更新索引，指向下一个位置
    oldStartVNode = prevChildren[++oldStartIdx]
    newStartVNode = nextChildren[++newStartIdx]
  } else if (oldEndVNode.key === newEndVNode.key) {
    // 省略...
  } else if (oldStartVNode.key === newEndVNode.key) {
    // 省略...
  } else if (oldEndVNode.key === newStartVNode.key) {
    // 省略...
  }
}

未命中四种策略，遍历旧节点列表

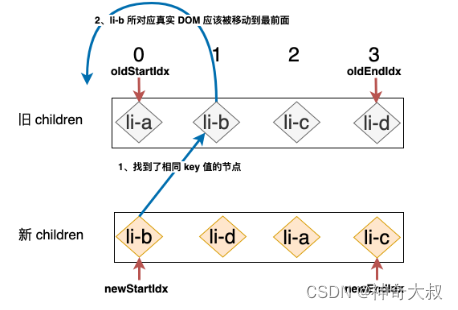
在这里插入图片描述

  • 上图中 ①、②、③、④ 这四步中的每一步比对，都无法找到可复用的节点
  • 策略为：拿新 children 中的第一个节点尝试去旧 children 中寻找，试图找到拥有相同 key 值的节点
  • 如果在旧的 children 中找到了与新 children 中第一个节点拥有相同 key 值的节点，这意味着：旧 children 中的这个节点所对应的真实 DOM 在新 children 的顺序中，已经变成了第一个节点。所以我们需要把该节点所对应的真实 DOM 移动到最前头
    在这里插入图片描述
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  if (oldStartVNode.key === newStartVNode.key) {
    // 省略...
  } else if (oldEndVNode.key === newEndVNode.key) {
    // 省略...
  } else if (oldStartVNode.key === newEndVNode.key) {
    // 省略...
  } else if (oldEndVNode.key === newStartVNode.key) {
    // 省略...
  } else {
    // 遍历旧 children，试图寻找与 newStartVNode 拥有相同 key 值的元素
    const idxInOld = prevChildren.findIndex(
      node => node.key === newStartVNode.key
    )
    if (idxInOld >= 0) {
      // vnodeToMove 就是在旧 children 中找到的节点，该节点所对应的真实 DOM 应该被移动到最前面
      const vnodeToMove = prevChildren[idxInOld]
      // 调用 patch 函数完成更新
      patch(vnodeToMove, newStartVNode, container)
      // 把 vnodeToMove.el 移动到最前面，即 oldStartVNode.el 的前面
      container.insertBefore(vnodeToMove.el, oldStartVNode.el)
      // 由于旧 children 中该位置的节点所对应的真实 DOM 已经被移动，所以将其设置为 undefined
      prevChildren[idxInOld] = undefined
    }
    // 将 newStartIdx 下移一位
    newStartVNode = nextChildren[++newStartIdx]
  }
}
  • 因为旧节点已经找到并处理过了，所以后续的双端比较需要跳过处理过的节点
  • 将旧 children 中的 li-b 节点变成 undefined，然后旧节点指针遇到时跳过
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  // undefined 跳过
  if (!oldStartVNode) {
    oldStartVNode = prevChildren[++oldStartIdx]
  } else if (!oldEndVNode) { // undefined 跳过
    oldEndVNode = prevChildren[--oldEndIdx]
  } else if (oldStartVNode.key === newStartVNode.key) {
    // 省略...
  } else if (oldEndVNode.key === newEndVNode.key) {
    // 省略...
  } else if (oldStartVNode.key === newEndVNode.key) {
    // 省略...
  } else if (oldEndVNode.key === newStartVNode.key) {
    // 省略...
  } else {
    const idxInOld = prevChildren.findIndex(
      node => node.key === newStartVNode.key
    )
    if (idxInOld >= 0) {
      const vnodeToMove = prevChildren[idxInOld]
      patch(vnodeToMove, newStartVNode, container)
      prevChildren[idxInOld] = undefined
      container.insertBefore(vnodeToMove.el, oldStartVNode.el)
    }
    newStartVNode = nextChildren[++newStartIdx]
  }
}

新增情况一

  • 节点所在的双端不满足四种策略，也不满足能找到旧节点

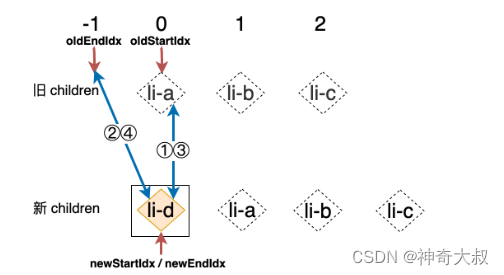
在这里插入图片描述

  • 在新 children 中，节点 li-d 是一个全新的节点。在这个例子中 ①、②、③、④ 这四步的比对仍然无法找到可复用节点，所以我们会尝试拿着新 children 中的 li-d 节点去旧的 children 寻找与之拥有相同 key 值的节点，结果很显然，我们无法找到这样的节点。这时说明该节点是一个全新的节点，我们应该将其挂载到容器中，由于 li-d 节点的位置索引是 newStartIdx，这说明 li-d 节点是当前这一轮比较中的“第一个”节点，所以只要把它挂载到位于 oldStartIdx 位置的节点所对应的真实 DOM 前面就可以了，即 oldStartVNode.el
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  if (!oldStartVNode) {
    oldStartVNode = prevChildren[++oldStartIdx]
  } else if (!oldEndVNode) {
    oldEndVNode = prevChildren[--oldEndIdx]
  } else if (oldStartVNode.key === newStartVNode.key) {
    // 省略...
  } else if (oldEndVNode.key === newEndVNode.key) {
    // 省略...
  } else if (oldStartVNode.key === newEndVNode.key) {
    // 省略...
  } else if (oldEndVNode.key === newStartVNode.key) {
    // 省略...
  } else {
    const idxInOld = prevChildren.findIndex(
      node => node.key === newStartVNode.key
    )
    if (idxInOld >= 0) {
      const vnodeToMove = prevChildren[idxInOld]
      patch(vnodeToMove, newStartVNode, container)
      prevChildren[idxInOld] = undefined
      container.insertBefore(vnodeToMove.el, oldStartVNode.el)
    } else {
      // 使用 mount 函数挂载新节点，如果传入了最后一个参数，内部也是使用 insertBefore
      mount(newStartVNode, container, false, oldStartVNode.el)
    }
    newStartVNode = nextChildren[++newStartIdx]
  }
}

新增情况二

  • 节点所在的双端优先满足了四种策略

在这里插入图片描述

  • 最终双端比较完成后结果
    在这里插入图片描述
  • oldEndIdx 将比 oldStartIdx 的值要小，对 oldEndIdx 和 oldStartIdx 的值进行检查，如果在循环结束之后 oldEndIdx 的值小于 oldStartIdx 的值则说明新的 children 中存在还没有被处理的全新节点，这时我们应该调用 mount 函数将其挂载到容器元素中，观察上图可知，我们只需要把这些全新的节点添加到 oldStartIdx 索引所指向的节点之前即可
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  // 省略...
}
if (oldEndIdx < oldStartIdx) {
  // 添加新节点
  for (let i = newStartIdx; i <= newEndIdx; i++) {
    mount(nextChildren[i], container, false, oldStartVNode.el)
  }
}

删除节点

在这里插入图片描述

  • 在进行双端比较后
    在这里插入图片描述
  • 此时 newEndIdx 的值小于 newStartIdx 的值，所以循环将终止，但是通过上图可以发现，旧 children 中的 li-b 节点没有得到被处理的机会，我们应该将其移除才行，循环结束后，一旦满足条件 newEndIdx < newStartId 则说明有元素需要被移除
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
  // 省略...
}
if (oldEndIdx < oldStartIdx) {
  // 添加新节点
  for (let i = newStartIdx; i <= newEndIdx; i++) {
    mount(nextChildren[i], container, false, oldStartVNode.el)
  }
} else if (newEndIdx < newStartIdx) {
  // 移除操作
  for (let i = oldStartIdx; i <= oldEndIdx; i++) {
    container.removeChild(prevChildren[i].el)
  }
}

双端比较的优势

  • 对于如下节点情况

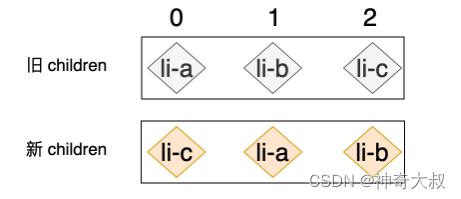
在这里插入图片描述

  • 如果采用 React 根据相对位置的diff 方式来对上例进行更新，则会执行两次移动操作
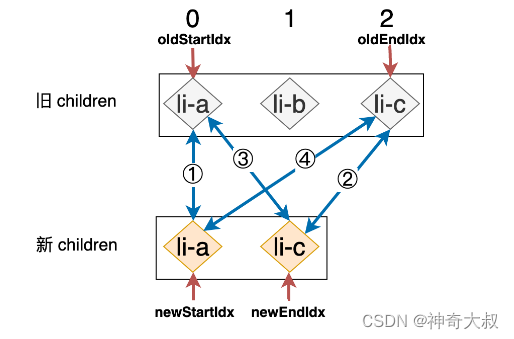
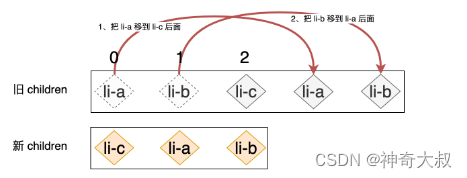
    • 首先会把 li-a 节点对应的真实 DOM 移动到 li-c 节点对应的真实 DOM 的后面
    • 接着再把 li-b 节点所对应的真实 DOM 移动到 li-a 节点所对应真实 DOM 的后面，即：
      在这里插入图片描述
  • 如果采用 vue 的双端比较 diff
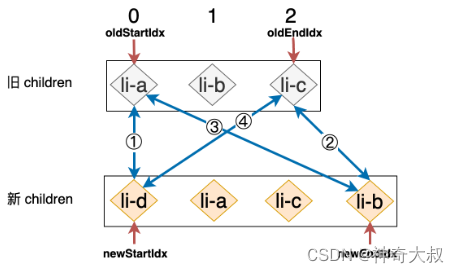
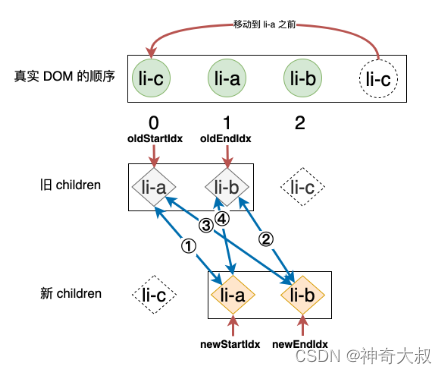
    • 第一步：拿旧 children 中的 li-a 和新 children 中的 li-c 进行比对，由于二者 key 值不同，所以不可复用，什么都不做。
    • 第二步：拿旧 children 中的 li-c 和新 children 中的 li-b 进行比对，不可复用，什么都不做。
    • 第三步：拿旧 children 中的 li-a 和新 children 中的 li-b 进行比对，不可复用，什么都不做。
    • 第四步：拿旧 children 中的 li-c 和新 children 中的 li-c 进行比对，此时，两个节点拥有相同的 key 值，可复用。

在这里插入图片描述

  • 可以看到，我们只通过一次 DOM 移动，就使得真实 DOM 的顺序与新 children 中节点的顺序一致，后序只需要 patch 不需要移动。双端比较更加符合人类思维，在移动 DOM 方面更具有普适性，能减少因为 DOM 结构的差异而产生的影响

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/838831.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

26 MFC序列化函数

26 MFC序列化函数

文章目录 Serialize对于存储文件的序列化 Serialize Serialize 是一个在 MFC (Microsoft Foundation Classes) 中常用的函数或概念。它用于将对象的数据进行序列化和反序列化&#xff0c;便于在不同的场景中保存、传输和恢复对象的状态。 在 MFC 中&#xff0c;Serialize 函数…
阅读更多...
如何查询显卡算力

如何查询显卡算力

感谢阅读 找到demo_suite此目录下打开控制台 找到demo_suite 一般在 C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v11.6\extras\demo_suite 这个目录 注意&#xff1a; 1.V后面的数字表示版本&#xff0c;请根据自己的版本进行更改 2.此目录为我的安装目录&#xff0…
阅读更多...
python批量检查folder中的文件是否符合要求

python批量检查folder中的文件是否符合要求

目录 问题描述&#xff1a; 问题解决&#xff1a; 问题描述&#xff1a; 最近在手动整理一些文档&#xff0c;要求是每一个folder以ID命名&#xff0c;每一个folder中存放三个内容&#xff08;如下图&#xff09;。如何实现批量检查每一个folder三个内容是否存在&#xff1f;…
阅读更多...
【2023年电赛国一必备】E题报告模板--可直接使用

【2023年电赛国一必备】E题报告模板--可直接使用

创作不易&#xff0c;麻烦关注CSDN【技术交流、免费报告资料】 通过百度网盘分享的文件&#xff1a;https://pan.baidu.com/s/1aXzYwLMLx_b59abvplUiYw?pwddn71 提取码:dn71 复制这段内容打开「百度网盘APP 即可获取」 任务 图1 任务内容 要求 图2 基本要求内容 图3 发挥部…
阅读更多...
K8s实战入门(三)

K8s实战入门(三)

文章目录 3. 实战入门3.1 Namespace3.1.1 测试两个不同的名称空间之间的 Pod 是否连通性 3.2 Pod3.3 Label3.4 Deployment3.5 Service 3. 实战入门 本章节将介绍如何在kubernetes集群中部署一个nginx服务&#xff0c;并且能够对其进行访问。 3.1 Namespace Namespace是kuber…
阅读更多...
【电源专题】充电IC与DC-DC有什么区别

【电源专题】充电IC与DC-DC有什么区别

充电IC和DC-DC一样使用很广泛，如手机、平板等需要电池供电的系统中，一般都会见到充电IC的身影。那么大家有没有考虑过一个问题。充电IC与DC-DC有什么区别？ 首先如下所示为充电IC的两个阶段，一个阶段是恒流充电阶段，我们一般称之为CC阶段，另一个是恒压充电阶段，我们称之为…
阅读更多...
Java课题笔记~ IoC 控制反转

Java课题笔记~ IoC 控制反转

二、IoC 控制反转 控制反转&#xff08;IoC&#xff0c;Inversion of Control&#xff09;&#xff0c;是一个概念&#xff0c;是一种思想。指将传统上由程序代码直接操控的对象调用权交给容器&#xff0c;通过容器来实现对象的 装配和管理。控制反转就是对对象控制权的转移&a…
阅读更多...
ShaderToy着色器移植到Three.js全过程记录

ShaderToy着色器移植到Three.js全过程记录

推荐&#xff1a;用 NSDT设计器 快速搭建可编程3D场景。 作为 Publicis Pixelpark Innovationlab 研究的一部分&#xff0c;我们研究了如何将较低底层的语言用于网络技术。 显而易见的选择似乎是 asm.js 或 WebAssembly。 但你也可以使用 WebGL 着色器来解决面向机器的问题。 …
阅读更多...
springboot+vue网红酒店客房预定系统的设计与实现_ui9bt

springboot+vue网红酒店客房预定系统的设计与实现_ui9bt

随着计算机技术发展&#xff0c;计算机系统的应用已延伸到社会的各个领域&#xff0c;大量基于网络的广泛应用给生活带来了十分的便利。所以把网红酒店预定管理与现在网络相结合&#xff0c;利用计算机搭建网红酒店预定系统&#xff0c;实现网红酒店预定的信息化。则对于进一步…
阅读更多...
【验证测试】未初始化的全局变量和局部变量的初值

【验证测试】未初始化的全局变量和局部变量的初值

验证目标&#xff1a; 未初始化的全局变量的初值为 0未初始化的局部变量的初值为随机值 测试用例&#xff1a; #include <stdio.h>char gval1; int gval2; static long gval3;int main() {unsigned char uchTmp1;unsigned int uTmp2;printf("%d\n", gval1)…
阅读更多...
Word中如何断开表格中线段

Word中如何断开表格中线段

Word中如何断开表格中线段_word表格断线怎么弄_仰望星空_LiDAR的博客-CSDN博客有时候为了美观&#xff0c;需要实现如下的效果&#xff0c;即第2条线段被断开成3段步骤如下&#xff1a;选中需要断开的格网&#xff0c;如下&#xff0c;再选择段落、针对下框标即可。_word表格断…
阅读更多...
Verilog学习记录-自用

Verilog学习记录-自用

always语句块一定条件写完整&#xff0c;否则电平触发&#xff0c;综合生成锁存器 task不可综合&#xff0c;主要用于仿真/验证 大部分都是并行执行的&#xff0c;只有begin end块中阻塞语句是串行 if-else和case的区别 if-else面积小&#xff0c;但时延&#xff08;执…
阅读更多...
Service not registered 异常导致手机重启分析

Service not registered 异常导致手机重启分析

和你一起终身学习&#xff0c;这里是程序员Android 经典好文推荐&#xff0c;通过阅读本文&#xff0c;您将收获以下知识点: 一、Service not registered 异常导致手机重启二、Service not registered 解决方案 一、Service not registered 异常导致手机重启 1.重启 的部分Log如…
阅读更多...
C++封装思想之二：友元机制和运算符重载（1W字详解）

C++封装思想之二：友元机制和运算符重载（1W字详解）

目录 友元机制和运算符重载 友元机制 友元函数 友元的作用 友元类 前置声明 友元类的注意事项 友元成员函数&#xff08;类的某个成员函数 作为另一个类的友元&#xff09; 运算符重载 运算符重载的作用 运算符重载的注意事项 运算符重载的实现 成员函数重载 友…
阅读更多...
2021-03-03 Multisim 14.0 电池充电防止反接保护

2021-03-03 Multisim 14.0 电池充电防止反接保护

R2R3当作充电线电阻看,也可设置这2个电阻导线电阻,电阻取值依据充电电流范围确定,由于电池存在电压因此可以用光耦检测,发光二极管当作继电器看,可采用继电器自锁,当下次再次反接的话另一个继电器同样,2个继电器相互控制.本电路可验证极性变化时2路检测的变化,图中S1为模拟电池…
阅读更多...
计算机视觉：替换万物Inpaint Anything

计算机视觉：替换万物Inpaint Anything

目录 1 Inpaint Anything介绍 1.1 为什么我们需要Inpaint Anything 1.2 Inpaint Anything工作原理 1.3 Inpaint Anything的功能是什么 1.4 Segment Anything模型&#xff08;SAM&#xff09; 1.5 Inpaint Anything 1.5.1 移除任何物体 1.5.2 填充任意内容 1.5.3 替换任…
阅读更多...
Finalshell连接Linux超时之Connection timed out: connect

Finalshell连接Linux超时之Connection timed out: connect

目录 &#x1f349;前言 &#x1f33c;报错 &#x1f33c;摸索 &#x1f4aa;解决措施 &#x1f349;前言 &#xff08;1&#xff09;福利&#xff1a;花了2小时才解决的BUG&#xff0c;希望本篇文章能帮你10分钟解决&#xff01; &#xff08;2&#xff09;tips&#xff1…
阅读更多...
6.s081/6.1810（Fall 2022）Lab3: page tables

6.s081/6.1810（Fall 2022）Lab3: page tables

文章目录 前言其他篇章参考链接0. 前置环境1. Speed up system calls (easy)1.1 简单分析1.2 映射1.3 页分配1.4 页释放1.5 测试 2. Print a page table (easy)2.1 简单分析2.2 实现2.3 测试 3. Detect which pages have been accessed (hard)3.1 简单分析3.2 实现3.2.1 获取参…
阅读更多...
DBSCAN聚类

DBSCAN聚类

一、概述 DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法&#xff0c;簇集的划定完全由样本的聚集程度决定。聚集程度不足以构成簇落的那些样本视为噪声点&#xff0c;因此DBSCAN聚类的方式也可以用于异常点的检测。 二、算法…
阅读更多...
一零六七、JVM梳理

一零六七、JVM梳理

JVM&#xff1f; Java虚拟机&#xff0c;可以理解为Java程序的运行环境&#xff0c;可以执行Java字节码&#xff08;Java bytecode&#xff09;并提供了内存管理、垃圾回收、线程管理等功能 java内存区域划分?每块内存中都对应什么? 方法区&#xff1a;类的结构信息、常量池、…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023