题目
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

思路
一.暴力法:
class Solution{
public int findKthLargest(int[] nums){
int len = nums.length;
Arrays.sort(nums);
return nums[len - k];
}
}
二:优先队列(堆)
「优先队列」主要能解决两个问题:
- 用来排序(堆排序)
以大根堆(升序)为例:
(1)首先将待排序数组构造成一个大根堆(每次插入新结点和父节点对比,不断向上调整,保证大根堆结构,注意要按照顺序插,不能左子树为空直接插在右子树的位置 ),此时数组最大值就是堆顶元素
(2)将堆顶元素和末尾元素交换,此时数组最大值就是末尾元素,剩余待排序元素个数为n-1
(3)将剩余的n-1个数再构造成大根堆(向下调整),再讲堆顶元素和n-1位置的元素交换,反复进行,最终得到有序数组
这里给个堆排序例子:
1.构造堆:每次插入新结点和父节点对比,保持大根堆特性
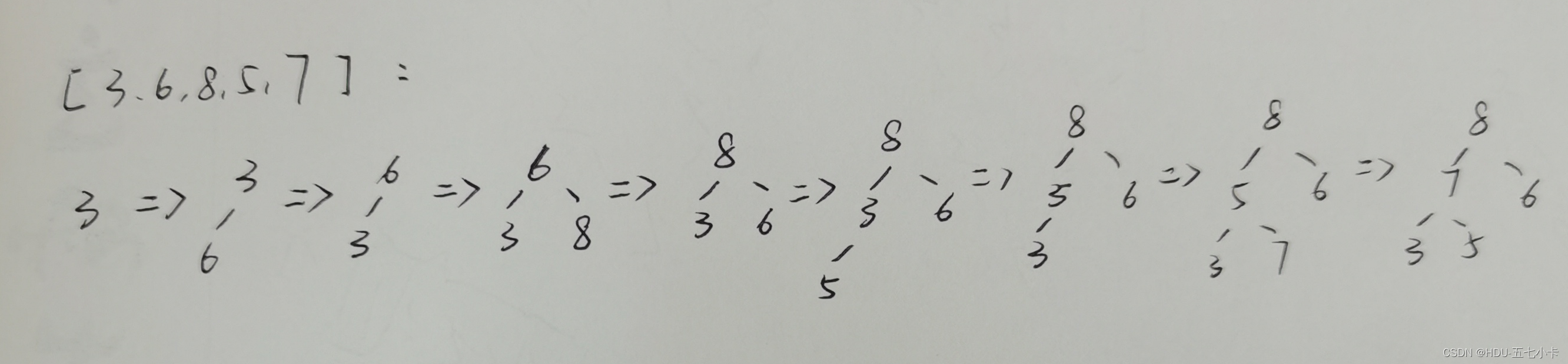
2.堆首尾交换最大值再构造堆:将最大值固定到末尾,将剩余的数继续构造成大根堆
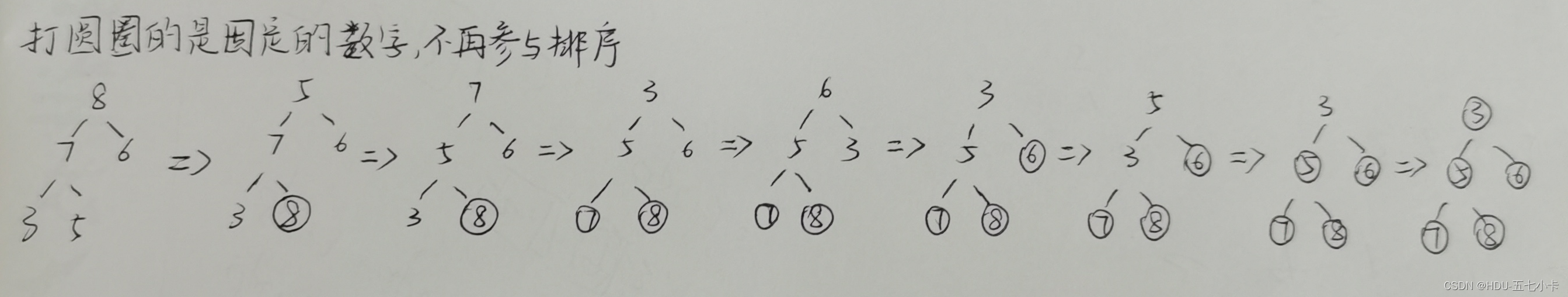
- 用来解决TopK问题(找出前/第k个最大/最小的元素)
(1)小根堆(根节点最小)用于降序排序,所以求最大的前k个数用小根堆
(2)大根堆(根节点最大)用于升序排序,所以求最小的前k个数用大根堆
☆注意点:java自带的优先队列PriorityQueue默认自然排序(升序)是小根堆,要区分一个东西,小根堆用于降序排序(因为根节点是最小的,所以固定的末尾值是最小的,最后的顺序就是降序),但是用优先队列实现小根堆要用升序定义,因为优先队列是升序时才能保证先出的是最小值(即小根堆中每次固定最小值,保证最终是降序排序的序列)
回到本题,本题中要求的是求出第k大的元素,因此建立一个有k个元素的小根堆,根据当前队列元素个数或当前元素与栈顶元素的大小关系进行分情况讨论:
- 当优先队列元素不足 k 个,可将当前元素直接放入队列中
- 当优先队列元素达到 k 个,并且当前元素大于栈顶元素(栈顶元素必然不是答案),可将当前元素放入队列中,然后内部调整堆结构
- 最终取堆顶元素就是答案(因为小根堆的堆顶是最小值,左右节点均大于根节点,而容量为k个元素,说明前面有k-1个元素比根节点大,即满足了第k大的元素这个要求)
java代码如下:
class Solution {
public int findKthLargest(int[] nums, int k){
PriorityQueue<Integer> q = new PriorityQueue<>((a,b) -> a - b);//升序定义优先队列,实现小根堆
for(int x : nums){
if(q.size() < k || q.peek() < x){
q.add(x);
}
if(q.size() > k){
q.poll();
}
}
return q.peek();
}
}
三:快速选择算法: 借助快排的子过程partition的分治操作
「快速选择」 是基于 「快速排序」 思想的用于解决TopK问题的算法,「快速选择」可以通过一次遍历,确定一个元素在排序以后的位置
对于给定数组,求解第 k 大元素,且要求线性复杂度O(n),正解为使用「快速选择」做法
基本思路与「快速排序」一致,每次敲定一个基准值 x,根据当前与 x 的大小关系,将范围在 [l,r] 的 nums[i] 划分为到两边
同时利用,利用题目只要求输出第 k 大的值,而不需要对数组进行整体排序,只需要根据划分两边后,第 k 大数会落在哪一边,来决定对哪边进行递归处理即可
java代码如下:
class Solution {
int[] nums;
int quickSelect(int l, int r,int k){
if(l == r){
return nums[k];
}
int x = nums[l];//基准枢轴
int i = l - 1;
int j = r + 1;
//以升序为例
while( i < j){
do{
i++;//从前往后找,找到第一个比基准元素大的位置
} while(nums[i] < x);
do{
j--;//从后往前找,找到第一个比基准元素小的位置
} while(nums[j] > x);
if(i < j) swap(i,j);//交换i和j的位置
}
if( k <= j){//如果k在前半区间,因为j和i交换了位置
return quickSelect(l, j, k);
} else {//如果k在后半区间
return quickSelect(j+1, r, k);
}
}
void swap(int i, int j){
int c = nums[i];
nums[i] = nums[j];
nums[j] = c;
}
public int findKthLargest(int[] nums, int k){
this.nums = nums;//需要将外界的题目中的nums作为参数传入进来
int n = nums.length;
return quickSelect(0, n-1, n-k);
}
}