例 1 对角线输出：

已知一个n*n的矩阵（n<=20），把矩阵二条对角线上的元素值加上10，然后输出这两条新对角线上的所有元素之和。

注意当n为奇数时两条对角线交叉的那个元素改变时只需要改变一次，累加的时候需要累加两次

输入格式

第一行为一个整数n（n<=20）

第二行开始为一个n*n个整数组成的矩阵，整数范围（1-1000）

输出格式

输出一个整数，为矩阵两条新对角线上的元素之和

输入样例：

6
1 1 1 1 1 1
2 2 2 2 2 2
3 3 3 3 3 3
4 4 4 4 4 4
5 5 5 5 5 5
6 6 6 6 6 6
 

输出样例：

162

示例1：图为N = 6的矩阵，将两条对角线上的元素输出1，其余位置输出0

 

提示：使用二维数组存储矩阵元素，问题的核心是找出两条对角线所包含元素位置的规律。

分析：

① 右斜线（\）：行=列，都从1到6(N)

 

a[1][1]
a[2][2]
...
a[6][6]

② 左斜线（/）：行+列 = 7(N+1)

a[1][6]
a[2][5]
...
a[6][1]

代码详情：

const int N=25;//将N设置成固定不变的常量
int n,ans,a[N][N];
int main()
{
  cin>>n;
  for(int i=1; i<=n; i++)
  {
    for(int j=1; j<=n; j++)
    {
      cin>>a[i][j];
    }
  }
  for(int i=1; i<=n; i++)
  {
    ans+=a[i][i];       //累加右对角线元素
    ans+=a[i][n+1-i];   //累加左对角线元素
  }
  ans+=2*n*10;          //总共2n个元素，每个元素都+10
  return 0;
}

示例2：杨辉三角

杨辉三角是一个由数字排列成的三角形表，一般形式如下：

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

（第一列和每行最后一列都为1，其余数字为它的左上方和正上方数字之和）

输入一个正整数n(n≤20)，表示三角形的行数，输出杨辉三角的第n行。

输入格式

输入一个整数n(n≤20)

输出格式

输出杨辉三角的第n行

输入样例：

6

输出样例：

1 5 10 10 5 1

 

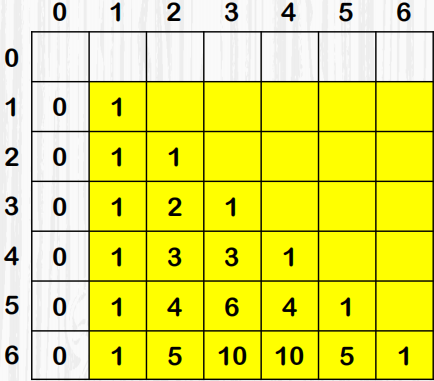
杨辉三角具有以下特性：(关注黄色标注部分)

① 第1列元素的值全为1。

② 第i行拥有i个元素，即：第i行有i列。

③ 元素(i, j)通过元素(i-1, j-1)和(i-1, j)累加获得，即：a[i][j] = a[i-1][j-1] + a[i-1][j]。

④ 如果第0列元素全为0，那么第1列元素也满足特性③。

解题步骤：

① 定义二维数组a[N][N]存储杨辉三角，并初始化第0列为0(全局变量），a[1][1] = 1;

② 双层 for 循环，第 1 层for循环枚举行 i（2到N），第2层for循环枚举列 j（1到i）;

③ 利用公式：a[i][j] = a[i-1][j-1] + a[i-1][j]，计算a[i][j]的值。

④ 输出第N行的第1列到第N列。

const int N=101;
int n,a[N][N];
int main()
{
        cin>>n;
        a[1][1]=1;//第一行第一列：1
        for(int i=2; i<=n; i++)
        {
                for(int j=1; j<=i; j++)//行与列相等
    {
      a[i][j]=a[i-1][j-1]+a[i-1][j];
    }
  }
  for(int j=1; j<=n; j++)
  {
    cout<<a[n][j]<<" ";
  }
  return 0;
}