题目大意

$(0\le a_i\le 1),(1\le cos{t}_i\le 10^9)$

题解

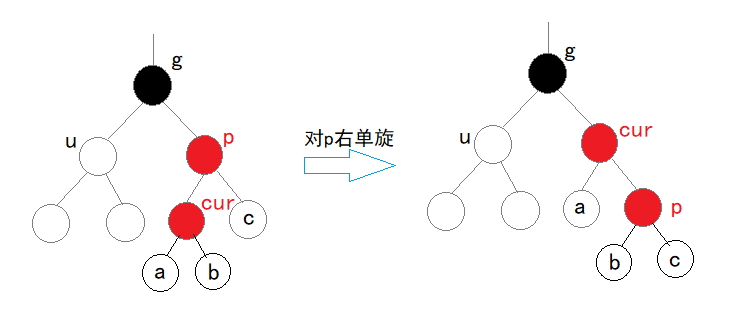
提供一种新的算法，kruskal重构树。
该算法重新构树，按边权排序每一条边后，
新建一个点为“两边的节点所在最大节点”的父节点，该点点权为该边边权。
该树有一些特征：
①：是一个二叉树。
③：原节点全部为叶节点。
②：两个节点的LCA的点权就是其原最短路径的最大边权。
具体 Kruskal 算法学习
建树可以用并查集计算。
了解了这个算法我们再看问题，要求最大边权，这点可以用kruskal维护。
对于某个不为叶节点的节点 $x$ ，它左儿子与右儿子匹配的黑白节点的最大边权显然为 $w_x$ 。
显然的，我们可以枚举左右儿子节点中的黑白节点个数，乘上点权，即为该点的贡献。
我们发现答案可以通过 $dfs$ 顺序从下往上来求解，且不会造成前效性，所以树形DP可以很好的解决这道题。
设 $d{p}_{x,b}$ 表示在 $x$ 的子树内有 $b$ 个黑色节点的最优解。
$$d{p}_{x,b}=max(d{p}_{son,black1}+d{p}_{son,b2}+w_x\ast (black1\ast white2+black2\ast white1))$$
white/black_1/2表示1/2的子树中有几个白色/黑色节点
且black1+black2=b
我们发现枚举 $b$ 的黑白分布情况，最多需要合并 $min(su{m}_{sonl},su{m}_{sonr})$次，
不然的话就需要从大的部分取一部分给数量少的一颗子树。
特殊的，对于叶节点
$$d{p}_{x,b}=(w_x==b\stackrel{ˆ}{}1)\ast -cos{t}_x$$
剩下的就好处理多了，写个DFS遍历一下即可处理。
计算时间复杂度，对于kruskal重构树，合并时长度最大为 $lo{g}_n$
即时间复杂度为 $O(N^{2}lo{g}_N)$ 可以通过。

参考代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e3+5;
const int inf=1e18+7;
struct node{
    int x,y,w;
}f[N];
int fa[N],cost[N];
int w[N];
int n,m,t,ans;
int sonl[N],sonr[N];
int sum[N];
int dp[N][3000];
void dfs(int x)
{
    if(x<=n)                   //叶节点
    {
        dp[x][0]=(w[x]==1)*(-cost[x]);
        dp[x][1]=(w[x]==0)*(-cost[x]);
//        cout<<x<<" "<<0<<" "<<dp[x][0]<<endl;
//        cout<<x<<" "<<1<<" "<<dp[x][1]<<endl;
        sum[x]=1;
    }
    else
    {
        dfs(sonl[x]);
        dfs(sonr[x]);
        int res=min(sum[sonl[x]],sum[sonr[x]]);           //启发式合并平均复杂度为log_n
        sum[x]=sum[sonl[x]]+sum[sonr[x]];
        for(int i=0;i<=sum[sonl[x]];i++)
            for(int j=0;j<=sum[sonr[x]];j++)
                dp[x][i+j]=-inf;
        for(int i=0;i<=sum[sonl[x]];i++)           //枚举黑色节点个数
        {
            for(int j=0;j<=sum[sonr[x]];j++)              //DP转移
            {
                int s=dp[sonl[x]][i]+dp[sonr[x]][j]+w[x]*(i*(sum[sonr[x]]-j)+(sum[sonl[x]]-i)*j);
                dp[x][i+j]=max(dp[x][i+j],s);
                ans=max(ans,dp[x][i+j]);
            }
        }            
    }
}
int cmp(node a,node b)
{
    return a.w<b.w;
}
int sf(int x)
{
    if(fa[x]==x)
        return x;
    return fa[x]=sf(fa[x]);
}
signed main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        scanf("%lld",&w[i]);
    for(int i=1;i<=n;i++)
        scanf("%lld",&cost[i]);
    for(int i=1;i<n;i++)
        scanf("%lld%lld%lld",&f[i].x,&f[i].y,&f[i].w);
    sort(f+1,f+n,cmp);
    t=n;
    for(int i=1;i<=2*n;i++)
        fa[i]=i;
    for(int i=1;i<n;i++)             //kruskal构树
    {
        int x=sf(f[i].x),y=sf(f[i].y);
        fa[x]=++t;
        fa[y]=t;
        w[t]=f[i].w;
        sonl[t]=x;
        sonr[t]=y;
    }
    dfs(t);
    printf("%lld",ans);
}