小程一言
这篇文章是在排序进行曲2.0之后的续讲,
这篇文章主要是对归并排序进行细致分析,以及操作。
希望大家多多支持
图片: 
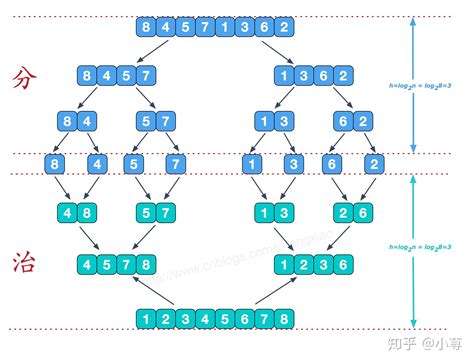
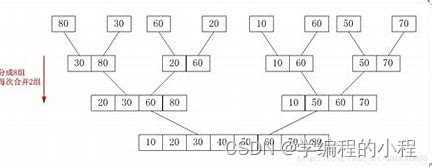
归并排序
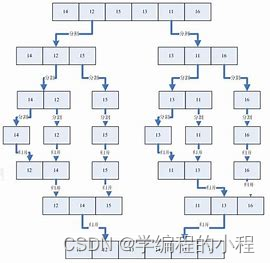
归并排序是一种分治算法,它将一个待排序的数组分成两个子数组,分别对这两
个子数组进行排序,然后再将
两个有序的子数组合并为一个有序的数组。这个过程不断地递归进行,直到最后
将整个数组排序完成。
步骤
分割(Divide):将待排序的数组不断地二分,直到分成单个元素的子数组。这个过程可以通过递归实现。递
归的终止条件是数组的长度为1。
合并(Merge):将相邻的两个有序子数组合并为一个有序的子数组。合并的方法是比较两个子数组的第一个元
素,将较小的元素放在新的子数组中,并将该元素从原子数组中移除。然后继续比较两个子数组的新的第
一个元素,重复这个过程,直到其中一个子数组为空。将剩余的另一个子数组直接拼接到新的子数组的
末尾。
递归合并(Recursive Merge):对每个单个元素的子数组进行排序和合并。当子数组长度为1时,它已经是有
序的,直接返回该子数组即可。对于长度大于1的子数组,先将其分割成两个子数组,然后分别对这两个子
数组进行递归合并,得到两个有序的子数组。最后将这两个有序的子数组进行合并,得到一个更大的有序
子数组。
举例
假设我们要对数组 [5, 3, 8, 2, 9, 1] 进行排序。
分割(Divide):首先将数组分成两个子数组,即 [5, 3, 8] 和 [2, 9, 1]。
递归合并(Recursive Merge):对两个子数组分别进行递归合并排序。首先对 [5, 3, 8] 进行递归合并排序,
得到有序子数组 [3, 5, 8]。然后对 [2, 9, 1] 进行递归合并排序,得到有序子数组 [1, 2, 9]。
合并(Merge):将两个有序子数组 [3, 5, 8] 和 [1, 2, 9] 进行合并。比较两个子数组的第一个元素,将
较小的元素放入新的子数组中,并将该元素从原子数组中移除。依次比较,得到新的子数组
[1, 2, 3, 5, 8, 9]。
最终,整个数组 [5, 3, 8, 2, 9, 1] 经过归并排序后,得到有序数组 [1, 2, 3, 5, 8, 9]。
总结
这个例子展示了归并排序的过程,通过不断地分割和合并子数组,最终将整个数组排序。在每一次合并过程中,
我们都是将两个有序的子数组合并为一个有序的子数组,这保证了最终得到的整个数组是有序的。

)### 复杂度分析
归并排序的时间复杂度为 O(nlogn),空间复杂度为 O(n)。
时间复杂度分析:
分割(Divide):每次将数组分割成两个子数组,分割的时间复杂度为 O(logn)。因为每次分割都将数组的大
小减半,所以需要进行 logn 次分割。
合并(Merge):对于每一次合并操作,需要比较两个子数组的元素并将较小的元素放入新的子数组中,合并的
时间复杂度为 O(n)。因为每次合并都是将两个子数组的元素全部比较一遍,所以需要进行 n 次合并。
递归合并(Recursive Merge):对于长度为 n 的数组,需要进行 logn 次递归合并,每次递归合并的时间
复杂度为 O(n)。所以总的时间复杂度为 O(nlogn)。
空间复杂度分析:
在每次递归合并的过程中,需要创建临时数组来存储合并后的子数组,临时数组的空间复杂度为 O(n)。
在每次递归合并完成后,临时数组会被销毁,所以整个归并排序的空间复杂度为 O(n)。
注意
归并排序是一种稳定的排序算法,因为在合并的过程中,如果两个元素相等,我们会先将左边的元素放入新的
子数组中,这样可以保持原始数组中相等元素的相对顺序不变。
应用场景
排序问题:归并排序可以用于对数组、链表等数据结构进行排序。它的时间复杂度为O(nlogn),在处理大规模
数据集时表现较好。
大规模数据的排序:归并排序适用于需要对大规模数据进行排序的场景。由于归并排序是一种分治算法,可以
将大规模数据分割成较小的子问题进行排序,然后再将排序好的子问题合并起来。
外部排序:归并排序是一种适用于外部排序的算法。外部排序是指需要处理的数据量大于计算机内存容量,需
要将数据存储在外部存储介质(如硬盘)中进行排序。归并排序的特点是每次只需要读取一部分数据到内
存中进行排序,然后将排序好的数据写回外部存储介质。
并行计算:归并排序可以通过并行计算的方式提高排序的效率。由于归并排序的分治特性,可以将大规模数据
分割成多个子问题进行排序,然后再将排序好的子问题合并起来。这种并行计算的方式可以利用多核处理
器或分布式计算环境来加速排序过程。
总结
归并排序适用于排序问题,特别是大规模数据的排序和外部排序场景。它具有稳定的时间复杂度和较好的并行
性能,因此在实际应用中被广泛使用。
实际举例
数组排序:归并排序可以用于对数组进行排序。例如,给定一个整数数组,可以使用归并排序将数组中的元素
按照升序进行排序。
链表排序:归并排序也可以用于对链表进行排序。例如,给定一个链表,可以使用归并排序将链表中的节点按
照升序进行排序。
文件排序:归并排序可以用于对大规模文件进行排序。例如,当需要对一个非常大的文件进行排序时,可以使
用归并排序算法将文件分割成多个较小的部分,分别对这些部分进行排序,然后再将排序好的部分合并起
来。
数据库排序:归并排序可以用于对数据库中的数据进行排序。例如,在某个数据库表中有大量的数据需要按照
某个字段进行排序,可以使用归并排序算法将数据分割成多个较小的部分,分别对这些部分进行排序,然
后再将排序好的部分合并起来。
外部排序:归并排序是一种适用于外部排序的算法。外部排序是指需要处理的数据量大于计算机内存容量,需
要将数据存储在外部存储介质(如硬盘)中进行排序。归并排序的特点是每次只需要读取一部分数据到内
存中进行排序,然后将排序好的数据写回外部存储介质。
Other
这些例子只是归并排序在实际中的一些应用,实际上归并排序的思想和方法也可以应用于其他问题,只需要将
问题分割成更小的子问题,并将子问题的结果合并起来。
代码实现
public class MergeSort {
public static void mergeSort(int[] arr) {
if (arr == null || arr.length <= 1) {
return;
}
int[] temp = new int[arr.length];
mergeSort(arr, 0, arr.length - 1, temp);
}
private static void mergeSort(int[] arr, int start, int end, int[] temp) {
if (start >= end) {
return;
}
int mid = start + (end - start) / 2;
mergeSort(arr, start, mid, temp);
mergeSort(arr, mid + 1, end, temp);
merge(arr, start, mid, end, temp);
}
private static void merge(int[] arr, int start, int mid, int end, int[] temp) {
int left = start;
int right = mid + 1;
int index = start;
while (left <= mid && right <= end) {
if (arr[left] <= arr[right]) {
temp[index++] = arr[left++];
} else {
temp[index++] = arr[right++];
}
}
while (left <= mid) {
temp[index++] = arr[left++];
}
while (right <= end) {
temp[index++] = arr[right++];
}
for (int i = start; i <= end; i++) {
arr[i] = temp[i];
}
}
public static void main(String[] args) {
int[] arr = {5, 2, 8, 4, 9, 1, 3, 7, 6};
mergeSort(arr);
System.out.println("Sorted array: " + Arrays.toString(arr));
}
}

结果
运行以上代码,输出结果为:Sorted array: [1, 2, 3, 4, 5, 6, 7, 8, 9],表示归并排序对给定的数组
进行了升序排序。
解释
在mergeSort方法中,首先判断数组的长度是否小于等于1,如果是,则直接返回。然后创建一个临时数组
temp,并调用mergeSort方法对数组进行递归排序。在mergeSort方法中,首先计算出数组的中间位置
mid,然后分别对左半部分和右半部分进行递归排序,最后调用merge方法将排序好的左右两部分合并起
来。在merge方法中,使用双指针分别指向左半部分和右半部分的起始位置,比较两个指针所指的元素大
小,将较小的元素放入临时数组temp中,并将对应指针向后移动一位。最后将临时数组temp中的元素复制
回原数组arr中,完成排序。
图片: