5.5树与二叉树的应用

5.5.1 哈夫曼树和哈夫曼编码

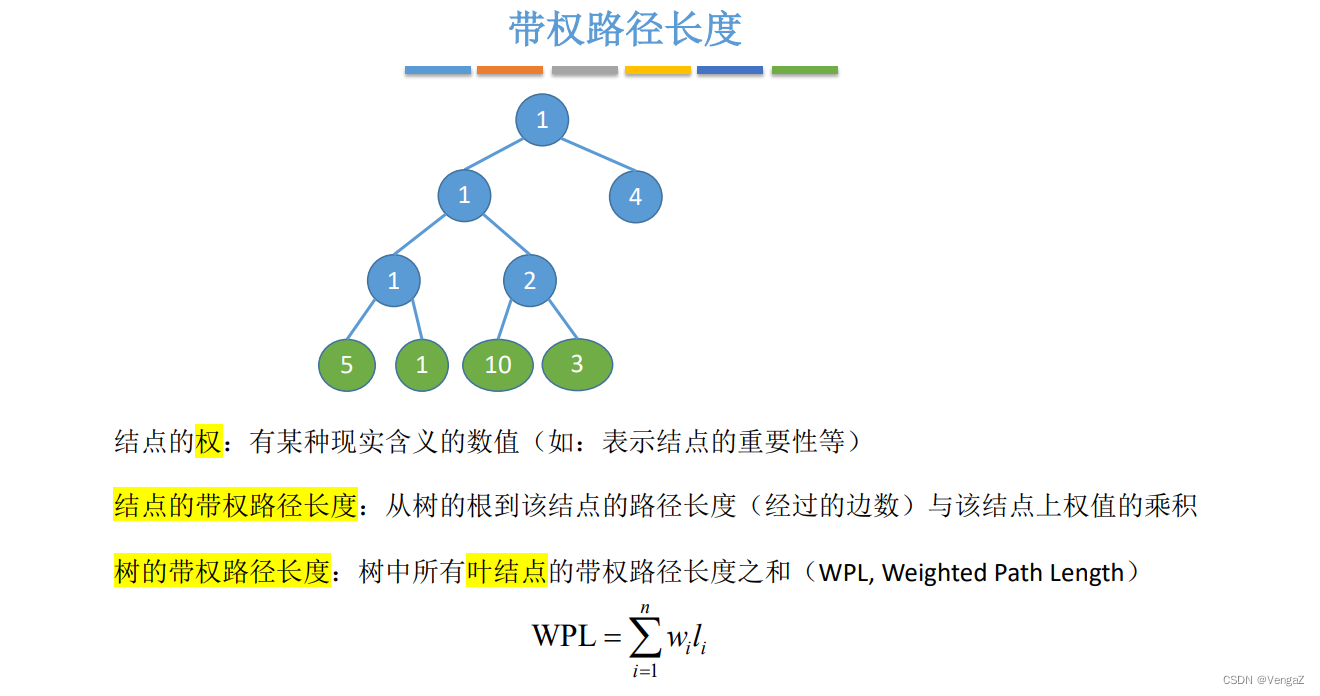
1. 带权路径长度的定义

权值大于零

2. 哈夫曼树的定义（最优二叉树，不唯一）

3. 哈夫曼树的构造

每次都选取权值最小的结点构成一棵树，并且新的树的根节点的权值为两个子结点的权值之和，重复这个步骤就能构成哈夫曼树

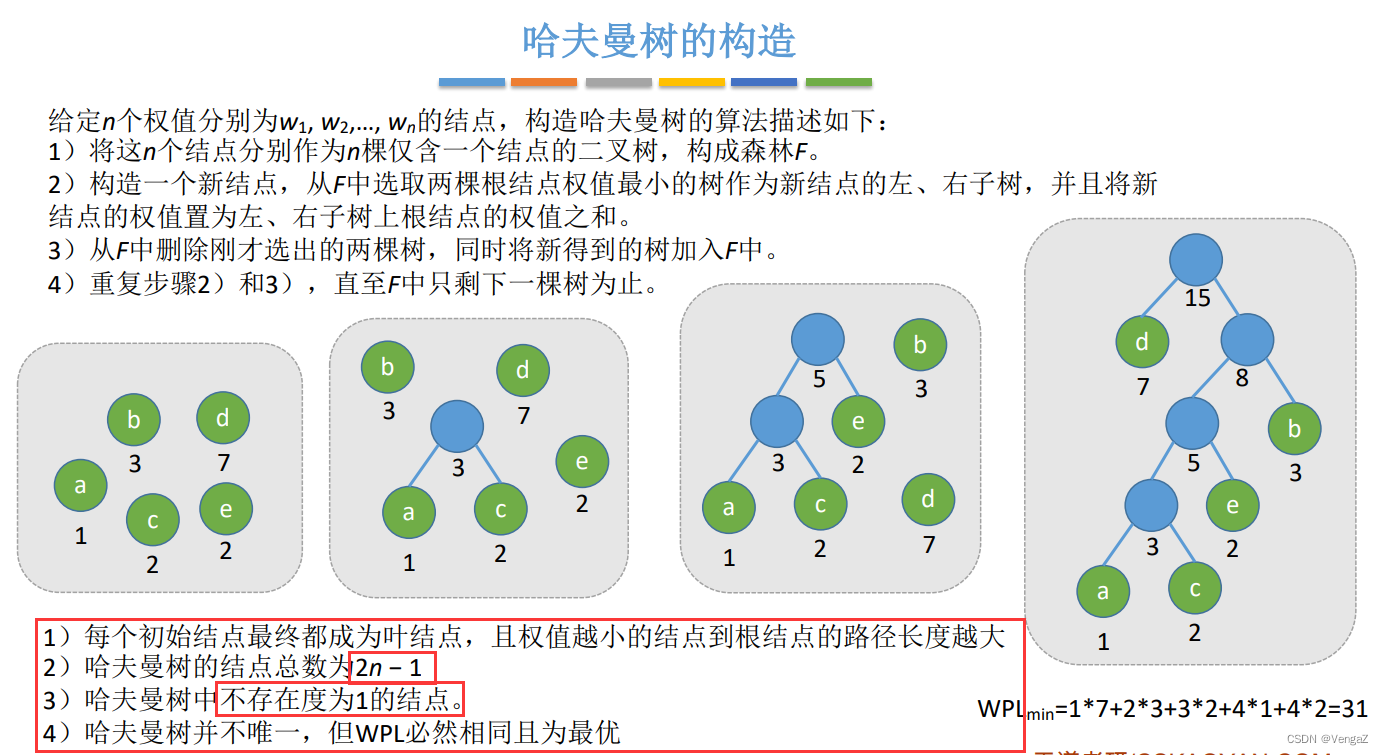
4. 哈夫曼树的特点

叶子结点n，度为二的结点n-1

5.哈夫曼编码（最短二进制前缀编码）

• 固定长度编码
  
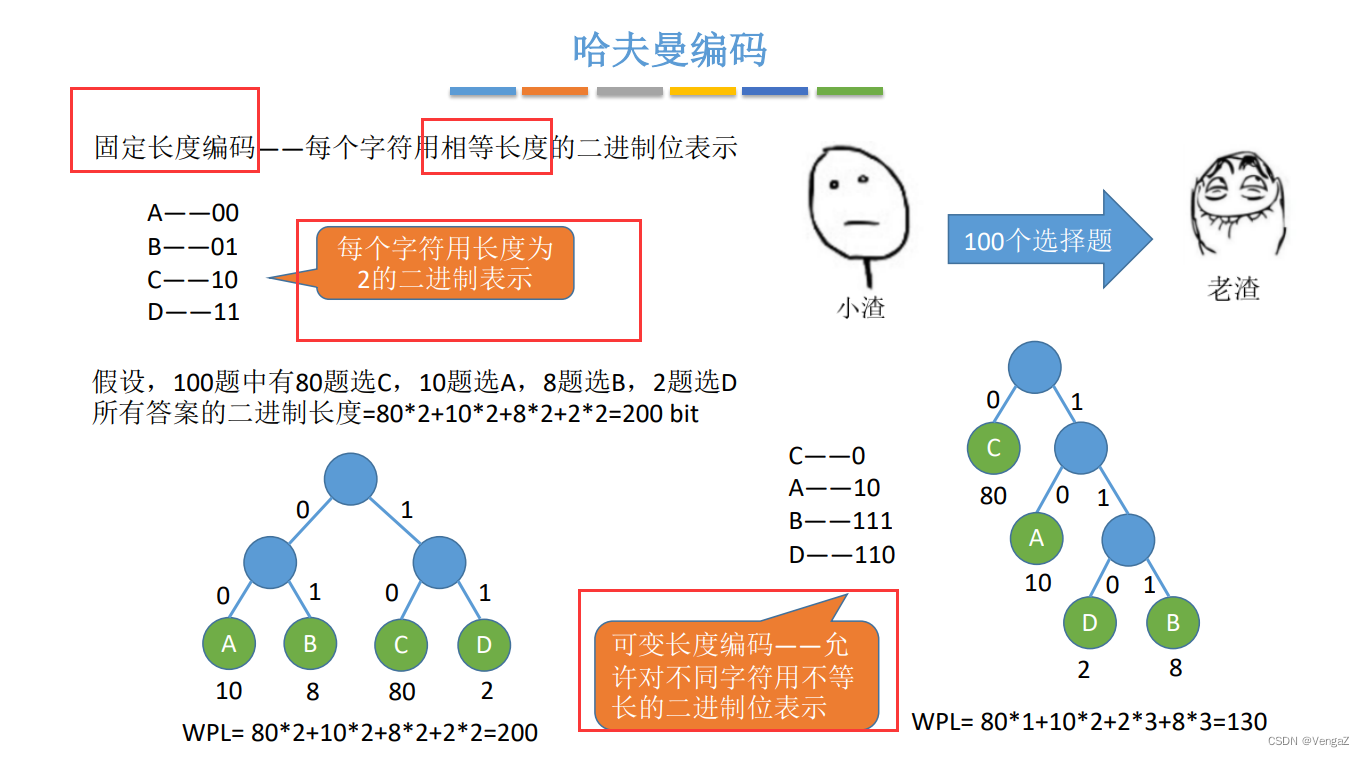
• 可变长度编码（无歧义）

数据结构：带权路径长度（Weighted Path Length）

在计算机科学中，带权路径长度（Weighted Path Length，简称WPL）是一种用于度量二叉树的平衡性的指标。它是通过将每个节点的深度与节点上的权值相乘，并将所有节点的权值之和作为二叉树的WPL。WPL在树的构建和优化中起着重要的作用，特别是在哈夫曼树和赫夫曼编码中有广泛应用。

1. 什么是带权路径长度

在二叉树中，每个节点都有一个权值，而节点的深度指的是从根节点到该节点的路径的长度（边的数量）。带权路径长度是将每个节点的深度与节点上的权值相乘，并将所有节点的权值之和作为二叉树的WPL。简而言之，WPL是树中所有路径长度与对应节点权值乘积的总和。

2. 计算带权路径长度

计算带权路径长度是一个简单而重要的过程。对于一个给定的二叉树，我们可以通过先序遍历或后序遍历的方式遍历树的每个节点，并计算每个节点的权值和深度的乘积，然后将所有节点的乘积相加即可得到WPL。

3. 应用：哈夫曼树和赫夫曼编码

带权路径长度在哈夫曼树和赫夫曼编码中有广泛的应用。哈夫曼树是一种特殊的最优二叉树，它的带权路径长度最小。在哈夫曼树中，权值较大的节点会位于树的较低层，而权值较小的节点会位于树的较高层，从而使得整个树的带权路径长度最小。赫夫曼编码是一种对字符进行编码的方法，它利用了哈夫曼树的特性，将出现频率较高的字符用较短的编码表示，而出现频率较低的字符用较长的编码表示，从而达到节省编码空间的目的。

4. 总结

带权路径长度是一种用于度量二叉树平衡性的重要指标，在计算机科学中有广泛的应用。通过将每个节点的深度与节点上的权值相乘，并将所有节点的权值之和作为二叉树的WPL，我们可以有效地评估树的结构是否平衡。特别是在哈夫曼树和赫夫曼编码中，带权路径长度的概念发挥了关键作用，帮助我们构建最优二叉树和高效的编码方案。

通过对带权路径长度的深入理解，我们可以更好地理解二叉树的结构和优化算法，并在解决实际问题中灵活运用。在学习数据结构和算法时，带权路径长度是一个重要的概念，值得我们深入学习和探索。

数据结构之哈夫曼树与哈夫曼编码

在计算机科学中，哈夫曼树（Huffman Tree）与哈夫曼编码（Huffman Coding）是数据压缩领域中常用的算法。它们能够将出现频率较高的字符用较短的编码表示，从而实现数据的高效压缩与解压缩。本文将详细介绍哈夫曼树与哈夫曼编码的原理与应用。

哈夫曼树

1. 基本概念

哈夫曼树是一种特殊的二叉树，它通过构建具有最小带权路径长度的二叉树来实现数据压缩。在哈夫曼树中，频率较高的字符将被赋予较短的编码，频率较低的字符将被赋予较长的编码。这样，编码后的数据可以达到最优的压缩效果。

2. 构建方法

构建哈夫曼树的基本方法是：首先将待编码的字符按照出现频率从小到大排列，然后不断合并出现频率最小的两个节点，直到所有节点都合并为一个根节点，形成哈夫曼树。在合并节点的过程中，将左子树的编码设为’0’，右子树的编码设为’1’，最终得到每个字符的哈夫曼编码。

3. 举例说明

假设有一个字符串"ABCDABCA"，其中字符A出现了3次，字符B出现了2次，字符C出现了2次，字符D出现了1次。我们可以使用哈夫曼树对该字符串进行编码：

• 将字符按照频率从小到大排列：D(1) < B(2) = C(2) < A(3)。
• 不断合并出现频率最小的两个节点，得到以下哈夫曼树：

       8
      / \
     3   5
    / \ / \
   D   A   B+C

• 对树中的左子树赋予’0’编码，右子树赋予’1’编码，得到字符的哈夫曼编码：

A: 1
B: 01
C: 00
D: 001

哈夫曼编码

1. 基本概念

哈夫曼编码是根据哈夫曼树得到的每个字符的编码。编码的长度与字符在哈夫曼树中的层数相关，出现频率较高的字符编码较短，出现频率较低的字符编码较长。通过对字符串进行哈夫曼编码，可以将原始数据进行高效压缩，从而减少数据的存储空间。

2. 编码方法

根据哈夫曼树的构建方法，每个字符的编码由根节点到对应字符的路径上的’0’和’1’组成。从根节点开始，沿着树的路径找到目标字符的叶子节点，记录所经过的’0’和’1’，即为该字符的哈夫曼编码。

3. 举例说明

以前面构建的哈夫曼树为例，得到的哈夫曼编码为：

• A: 1
• B: 01
• C: 00
• D: 001

将字符串"ABCDABCA"进行编码，得到的哈夫曼编码为：“10101000101000100”，经过哈夫曼编码后，原始字符串被压缩为较短的二进制编码，实现了数据的高效压缩。

应用与总结

哈夫曼树与哈夫曼编码在数据压缩与解压缩中有着广泛的应用。它们能够将出现频率较高的字符用较短的编码表示，从而实现对数据的高效压缩与解压缩。哈夫曼树和哈夫曼编码是一种简单而高效的数据压缩算法，在计算机科学和通信领域得到了广泛的应用。通过深入了解和掌握哈夫曼树与哈夫曼编码的原理与应用，我们可以更好地理解数据压缩的技术，提高数据处理的效率，为计算机科学和通信领域的发展做出贡献。