本文仅提取了课程的部分内容,原视频课程如下:姜三勇《电工学》暂态过程
电路暂态过程——产生的原因:
1、内部原因:电路内部含有储能元件(如:电容、电感),其中存储的能量不能发生改变。
就是说没有储能元件的电路是没有暂态过程的(如:纯电阻电路)
2、外部原因:电路工作过程中发生换路(电路的接通、断开、短路、元件参数或电源参数发生变化)
就是说即便有了储能元件,外部不发生换路,也是没有暂态过程的,此时电路是稳态
电路暂态过程——研究的目的:
1、利用:研究暂态过程的变化规律,产生所需要的信号(如:三角波、方波)
2、预防:避免暂态过程中可能出现的过高电压、过大电流,对电器设备和人身产生损害和伤害。
电路暂态过程——研究的内容:
1、总体任务:求解描述暂态电路激励与响应间关系的微分方程,并指出推导过程的物理意义。
2、具体任务:
1)、暂态过程何时开始——初始值f(0+)
2)、暂态过程何时结束——稳态值f(∞)
3)、暂态过程进行的快慢——时间常数t
4)、变化规律的描述——微分方程的解或曲线
内容研究方法——换路定律:
根据能量守恒定律,电路中储能元件电容C和电感L中储存的电场能Wc和磁场能Wl在换路前(t=0-)后(t=0+)瞬间不发生变化。即
C
:
W
C
=
1
2
C
u
C
2
(
0
−
)
=
1
2
C
u
C
2
(
0
+
)
L
:
W
L
=
1
2
C
i
L
2
(
0
−
)
=
1
2
C
i
L
2
(
0
+
)
\begin{align} & C:\begin{matrix} {} \\ \end{matrix}{{W}_{C}}=\frac{1}{2}Cu_{C}^{2}(0-)=\frac{1}{2}Cu_{C}^{2}(0+) \\ & L:\begin{matrix} {} \\ \end{matrix}{{W}_{L}}=\frac{1}{2}Ci_{L}^{2}(0-)=\frac{1}{2}Ci_{L}^{2}(0+) \\ \end{align}
C:WC=21CuC2(0−)=21CuC2(0+)L:WL=21CiL2(0−)=21CiL2(0+)
由此可得:
C
:
u
C
(
0
−
)
=
u
C
(
0
+
)
L
:
i
L
(
0
−
)
=
i
L
(
0
+
)
\begin{align} & C:\begin{matrix} {} \\ \end{matrix}{{u}_{C}}(0-)={{u}_{C}}(0+) \\ & L:\begin{matrix} {} \\ \end{matrix}{{i}_{L}}(0-)={{i}_{L}}(0+) \\ \end{align}
C:uC(0−)=uC(0+)L:iL(0−)=iL(0+)
也就是说,电容的电压和电感电流不能跳变,而电容电流和电感电压没有约束
当电容C和电感L为常数时,由电容电荷公式、电感磁链公式,可以推断得到电容电荷和电感磁通链不能突变(即电荷守恒、磁通守恒)
q
C
=
C
u
C
ψ
C
=
L
i
C
\begin{align} & {{q}_{C}}=C{{u}_{C}} \\ & {{\psi }_{C}}=L{{i}_{C}} \\ \end{align}
qC=CuCψC=LiC
也就是说,当电容、电感为常数时,换路前后的电荷、磁通不会突变
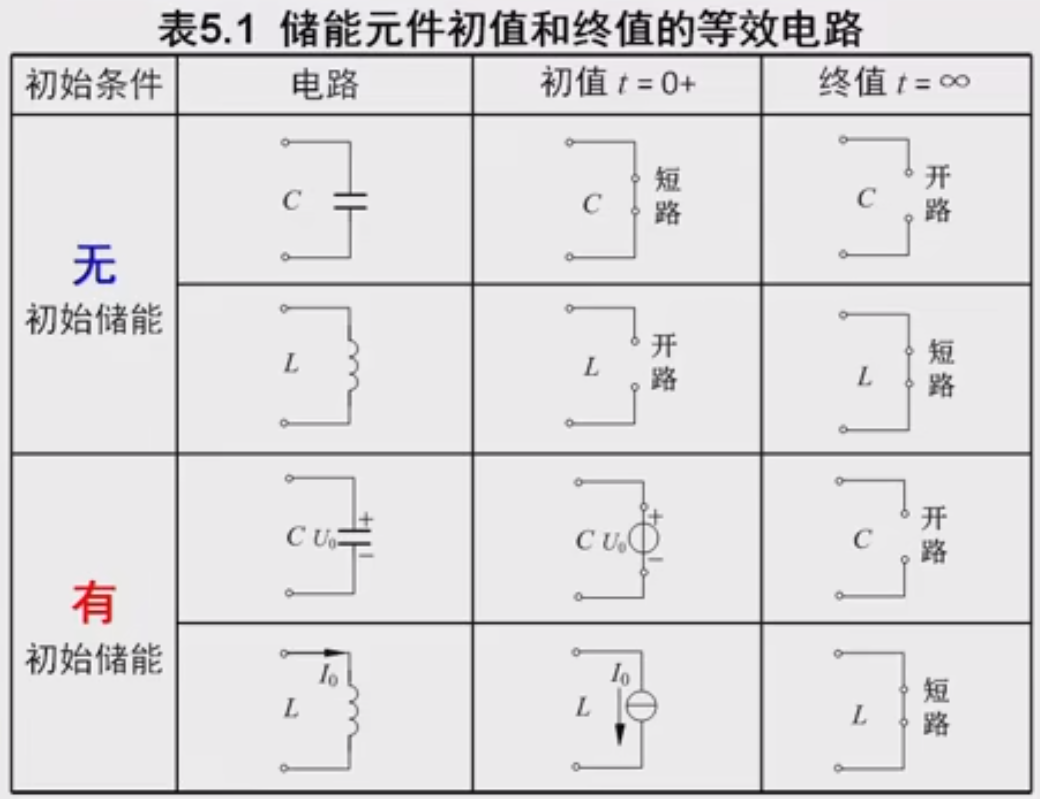
初始值f(0+)、稳态值f(∞)的确定
初始值f(0+)的确定:
a、由换路前电路求出Uc(0-)、Ic(0-)
b、由换路定律求出Uc(0+)、Ic(0+)
c、由换路后的电路,根据KCL、KVL和元件约束,求出其他电压和电流的初始值
注意:C中电流、L上电压、R中电压和电流可以突变
稳态值f(∞)的确定:
a、由换路后t=∞时的电路,可知C相当于开路,L相当于短路,即Ic(∞)=0和Ul(∞)=0
b、由换路后t=∞时的电路,根据KCL、KVL和元件约束,求出其他电压和电流的稳态值