概述
蜣螂优化算法由于其寻优速度和收敛精度,自2023年问世以来,热度一直很高。本篇文章对蜣螂算法进行改进,改进思路是参考2023年6月25号发表在知网的一篇文献(文献放在了文章末尾)。
改进的蜣螂优化算法融合了改进的正弦算法,自适应高斯-柯西混合变异扰动和Bernoulli混沌映射。
01原理简述
- 融合改进的正弦算法
改进正弦算法(MSA)策略是受到正余弦算法、正弦算法和指数正余弦算法函 数以 及 改进的正弦余弦算法等各类相关算法的启发,利用数学中的正弦函数进行迭代寻优, 具有较强的全局探索能力。同时在位置更新过程中引入自适应的可变惯性权重系数 使算法能够对局部区域进行充分搜索,使全局探索和局部开发能力达到良好的平 衡。改进正弦算法位置更新公式如下所示:
![]()
r1为非线性递减函数,r2是区间[0,2π]上的随机数,r3是区间[-2, 2]上的随机数。r1表达式如下:

![]()
为进一步改进 DBO算法协调全局的探索与局部开发 的能力,该文献引入了正弦引导机制,MSA 作为替代蜣螂正切跳舞的策略嵌入DBO算法,即在滚球阶段对整个蜣螂个体进行正弦的操作引导蜣螂位置更新,改进后的公式如下:

其实就是将蜣螂正切跳舞阶段的公式进行了改进,融合和正弦算法,然后对正弦算法的一些参数因子进行了改进。
-
融合自适应高斯-柯西混合变异扰动
在智能优化算法中引入变异算子,既可以增强种群的多样性,又可以使算法避免陷入局部极小,对每个个体进行变异扰动,然后比较其变异前后的位置,选择较好的位置进入下一次迭代,充分增加蜣螂的多样性,扩大种群搜索范围,具体公式如下:
![]()
- Bernoulli混沌映射策略
该文献采用 Bernoulli映射初始化蜣螂个体位置,先利用Bernoulli映射关系将所得的值投影到混沌变量空间内,然后将产生的混沌值通过线性变换映射到算法初始空间中,Bernoulli映射具体表达式为:
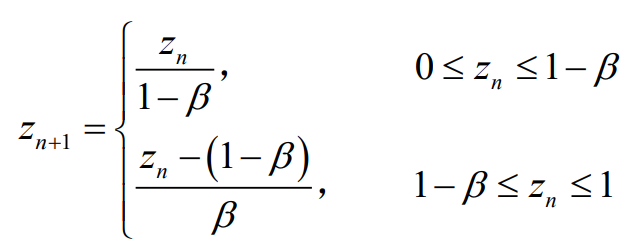
关于混沌映射,之前整理过十种混沌映射优化智能算法,新关注的童鞋可以参考一下这篇文章。。10种混沌映射优化灰狼算法,可一键切换,可用于优化所有群智能算法,以灰狼算法为例进行介绍
02 改进效果
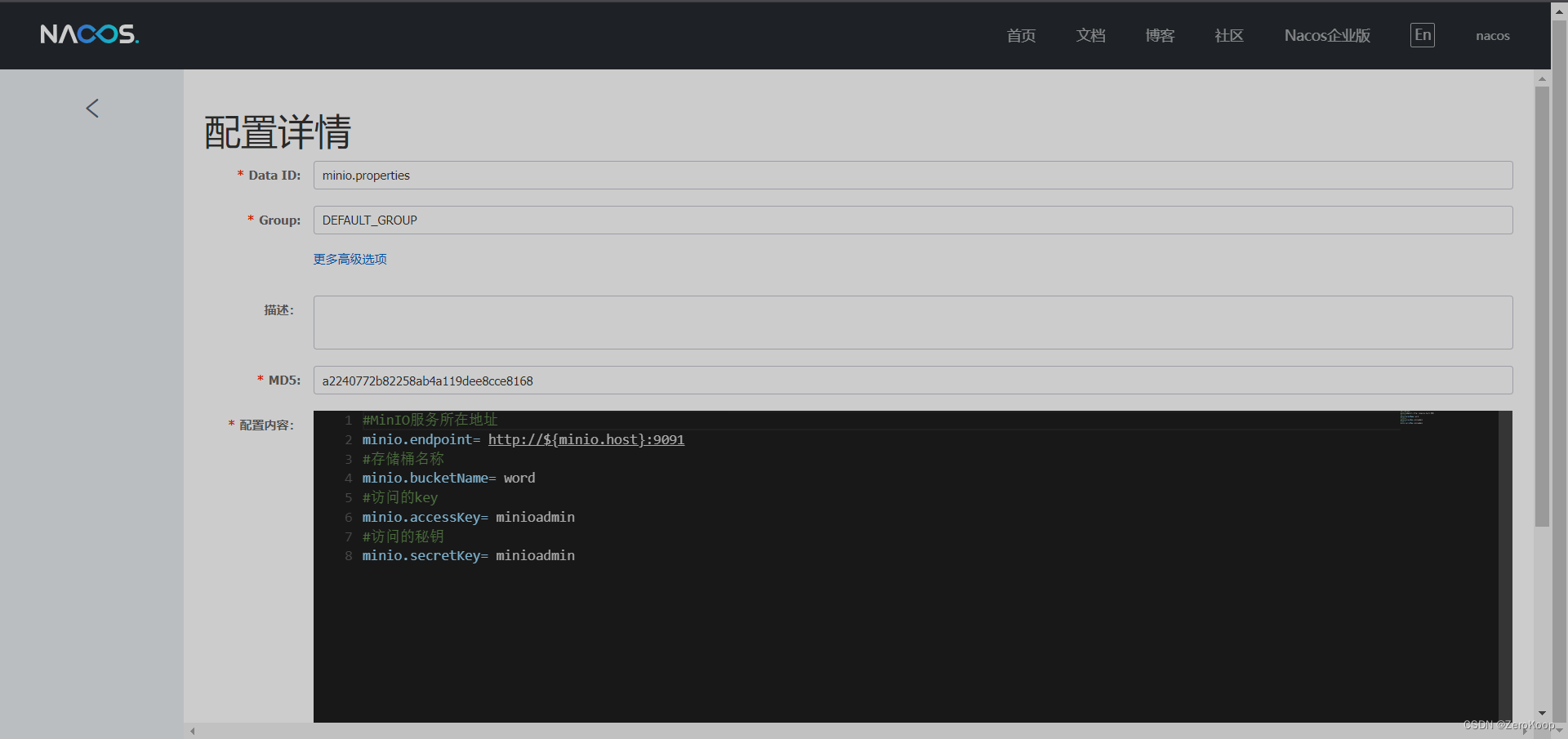
为了看出改进效果,作者同时与白鲸算法(BWO),麻雀算法(SSA),沙猫群优化算法(SCSO),蜣螂优化算法(DBO),以及改进正弦算法引导的蜣螂优化算法(MSADBO),一共五种算法进行对比。在CEC2005函数上测试,设置粒子个数为50,迭代次数为1000。截图前10个函数供大家参考。
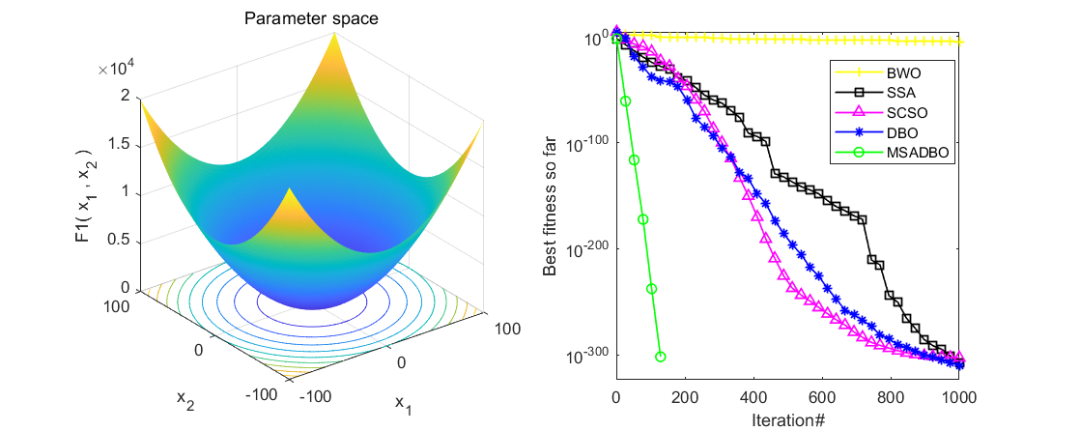
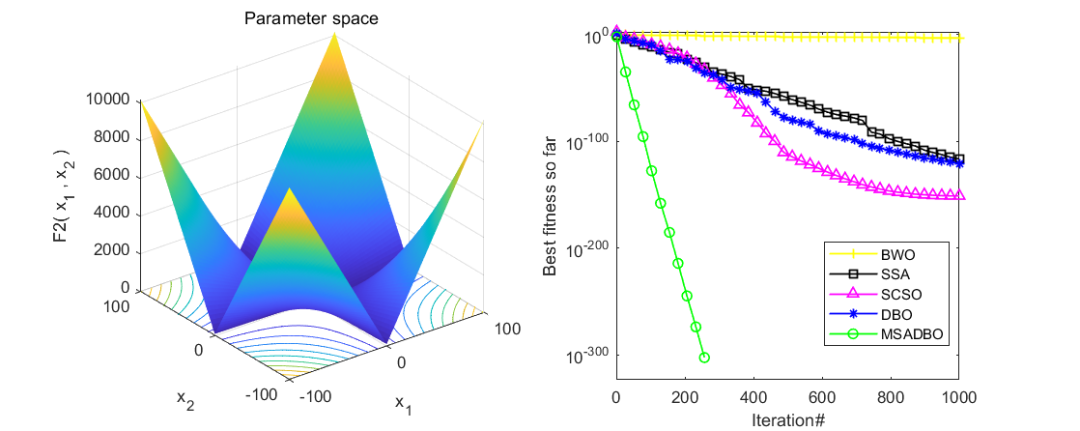
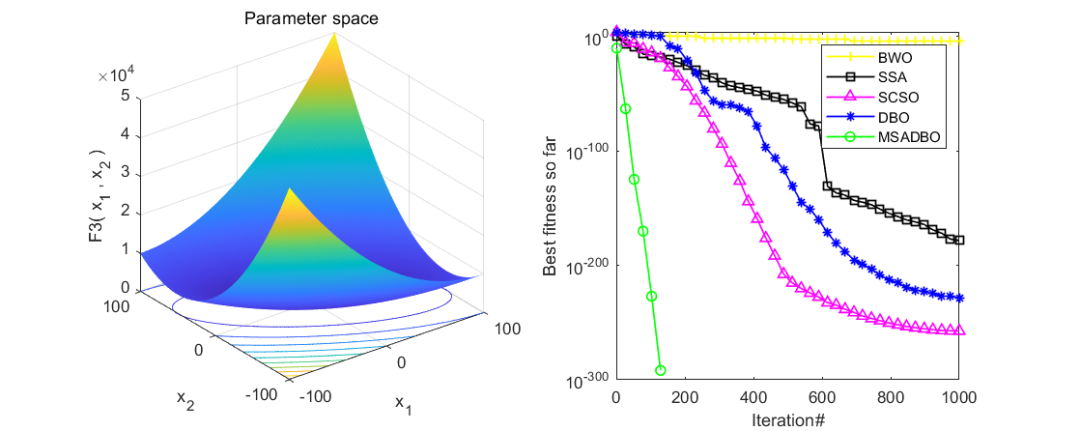
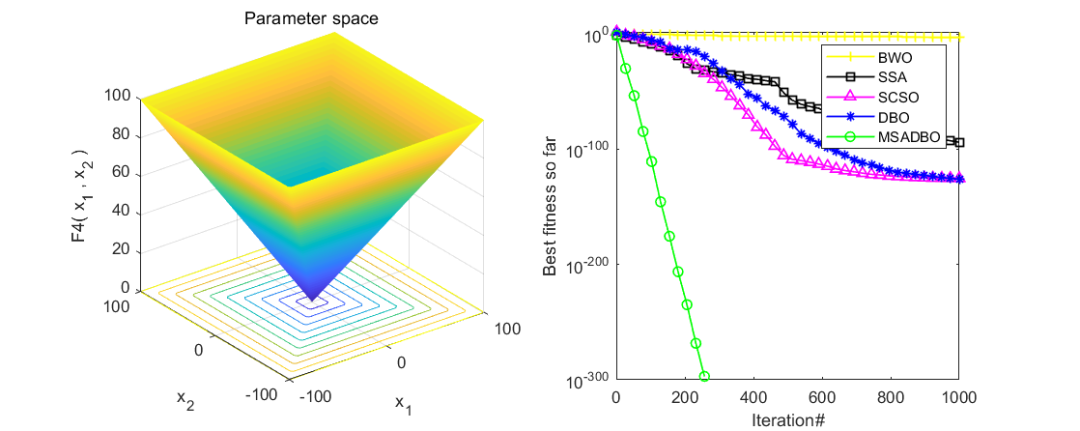
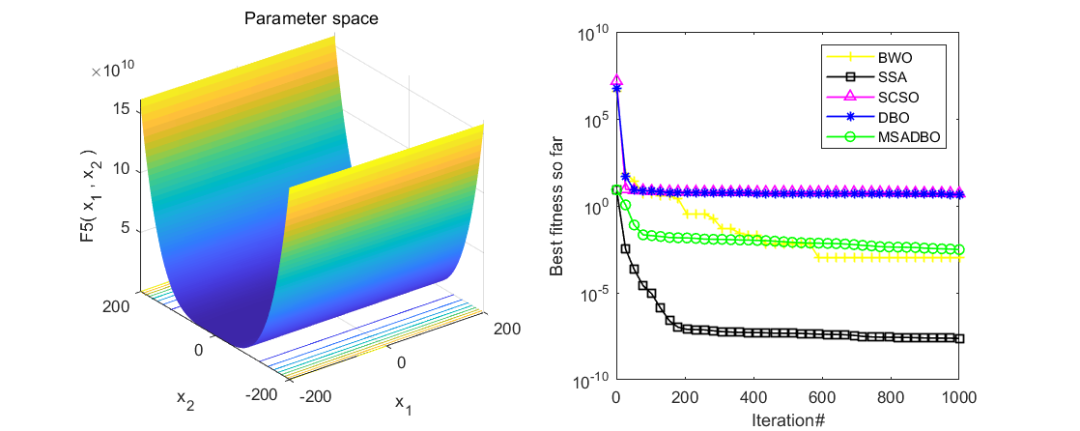
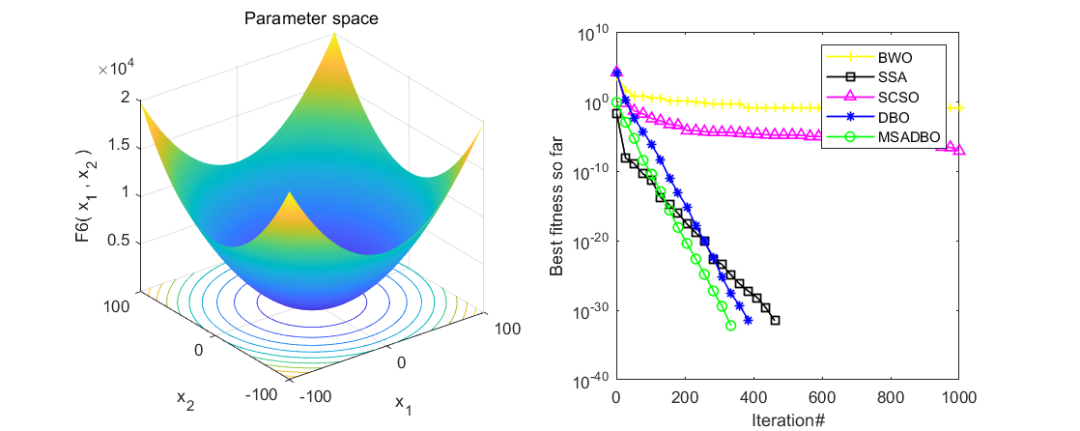


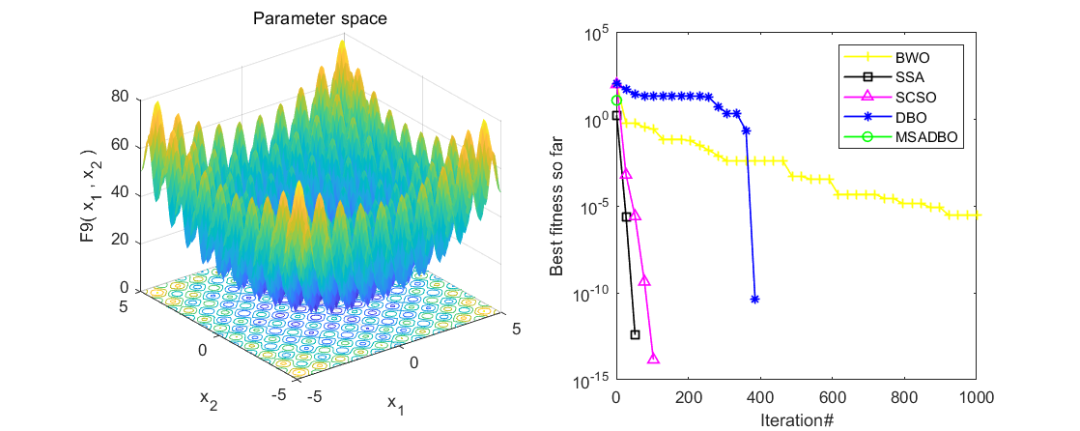
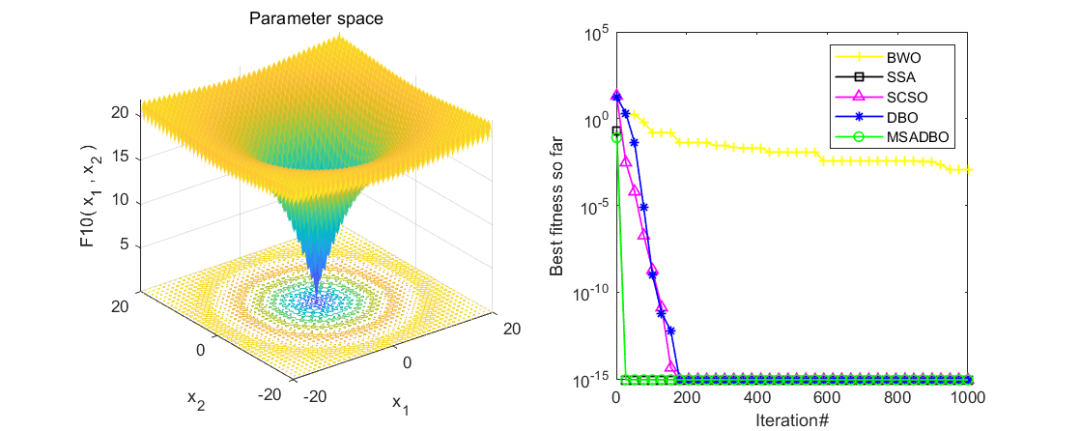
可以看到,改进正弦算法引导的蜣螂优化算法(MSADBO)表现还是非常不错的!除了第五个函比不上麻雀算法之外,其他九个函数效果都是十分不错的。
03核心代码展示
%% 淘个代码 %%
% 2023/07/20 %
%微信公众号搜索:淘个代码
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all
clc
close
PD_no=50; %Number of sand cat
F_name='F14'; %Name of the test function
Max_iter=1000; %Maximum number of iterations
[LB,UB,Dim,F_obj]=CEC2005(F_name); %Get details of the benchmark functions
%% BWO
[Best_pos,Best_score, BWO_cg_curve ] = BWO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call BWO
fprintf ('Best solution obtained by BWO: %s\n', num2str(Best_score,'%e '));
display(['The best optimal value of the objective funciton found by BWO for ' [num2str(F_name)],' is : ', num2str(Best_pos)]);
%% SSA
[Best_pos,Best_score, SSA_cg_curve ] = SSA(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call SSA
fprintf ('Best solution obtained by SSA: %s\n', num2str(Best_score,'%e '));
display(['The best optimal value of the objective funciton found by SSA for ' [num2str(F_name)],' is : ', num2str(Best_pos)]);
%% SCSO
[BsSCSO,BpSCSO,SCSO_cg_curve]=SCSO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call MSCSO
fprintf ('Best solution obtained by SCSO: %s\n', num2str(BsSCSO,'%e '));
display(['The best optimal value of the objective funciton found by SCSO for ' [num2str(F_name)],' is : ', num2str(BpSCSO)]);
%% DBO
[Best_pos,Best_score, DBO_cg_curve ] = DBO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call DBO
fprintf ('Best solution obtained by DBO: %s\n', num2str(Best_score,'%e '));
display(['The best optimal value of the objective funciton found by DBO for ' [num2str(F_name)],' is : ', num2str(Best_pos)]);
%% MSADBO
[MSADBOBest_pos,MSADBOBest_score, MSADBO_cg_curve ] = MSADBO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call MSADBO
fprintf ('Best solution obtained by MSADBO: %s\n', num2str(MSADBOBest_score,'%e '));
display(['The best optimal value of the objective funciton found by MSADBO for ' [num2str(F_name)],' is : ', num2str(MSADBOBest_pos)]);
%%
CNT=40;
k=round(linspace(1,Max_iter,CNT)); %随机选CNT个点
% 注意:如果收敛曲线画出来的点很少,随机点很稀疏,说明点取少了,这时应增加取点的数量,100、200、300等,逐渐增加
% 相反,如果收敛曲线上的随机点非常密集,说明点取多了,此时要减少取点数量
iter=1:1:Max_iter;
figure('Position',[154 145 894 357]);
subplot(1,2,1);
func_plot(F_name); % Function plot
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([F_name,'( x_1 , x_2 )'])
subplot(1,2,2); % Convergence plot
h1 = semilogy(iter(k),BWO_cg_curve(k),'y-+','linewidth',1);
hold on
h2 = semilogy(iter(k),SSA_cg_curve(k),'k-s','linewidth',1);
hold on
h3 = semilogy(iter(k),SCSO_cg_curve(k),'m-^','linewidth',1);
hold on
h4 = semilogy(iter(k),DBO_cg_curve(k),'b-*','linewidth',1);
hold on
h5 = semilogy(iter(k),MSADBO_cg_curve(k),'g-o','linewidth',1);
xlabel('Iteration#');
ylabel('Best fitness so far');
legend('BWO','SSA','SCSO','DBO','MSADBO');04参考文献
[1]潘劲成,李少波,周鹏等.改进正弦算法引导的蜣螂优化算法[J/OL].计算机工程与应用:1-21[2023-07-31].http://kns.cnki.net/kcms/detail/11.2127.TP.20230626.1952.024.html
05
代码获取,点击下方卡片,后台回复关键词:
MSADBO