有很多概念平时一直在说,但是具体的应用场景却一直不明确,这会导致我们在实际应用过程中对应该使用的方法不够明确,在此对常用的几种数据挖掘方法使用场景进行分类和整合。
数据降维
为什么要降维
- 数据稀疏,维度高
- 高维数据采用基于规则的分类方法
- 采用复杂模型,但是训练集数目较少(这一点很实用,对于少量的数据,又想使用相对复杂的需要大量数据集的模型(例如神经网络),首先通过数据降维减少影响的参数可以相同的模型训练成本大幅下降,仅需要少量训练数据集即可)
- 需要可视化
典型降维方法
PCA主成分分析法
大白话:将几个存在一定相关性的属性通过线性组合,形成一个组合属性替代原来的多个属性。
降数据
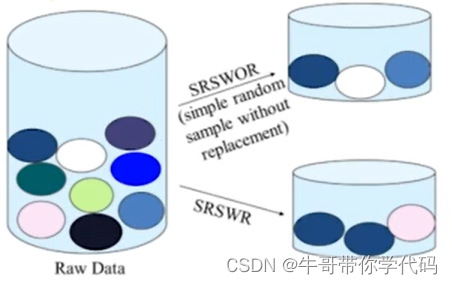
通过抽样(有放回或者无放回),来存储少量的数据。

抽取部分数据点时,也要选择恰当的数量的点,在不破坏原有结构的前提条件下。
数据压缩

通过降低图像像素中存储点的数量,来降低图像像素质量的同时减少图像的存储开销。
主成分分析用于数据降维
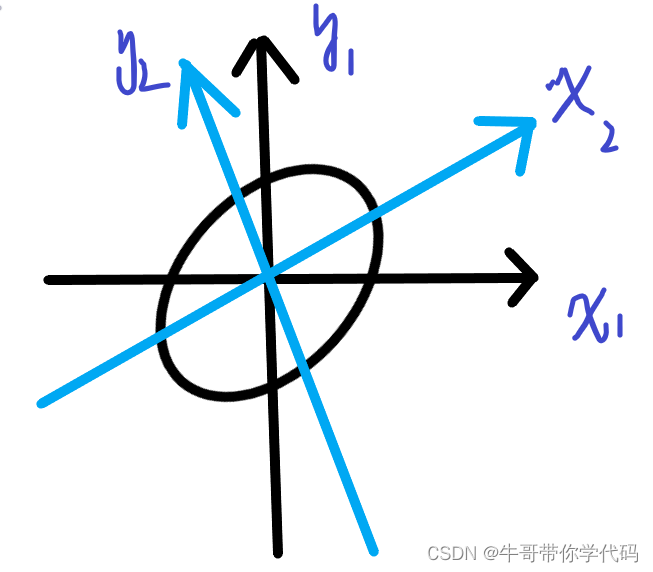
举个例子,上面的x1y2坐标系中的数据全部向x2y2坐标系进行投影,可以发现相应的贡献度中国x可以提供约为80%的贡献度,则可以使用相应的坐标系(损失20%贡献度可以忽略不计),来代替原有坐标系,用更少的参数代表尽可能高的贡献度
独立性检验:
定性对定量的影响:使用方差分析进行检验
定量对定量的影响:回归分析
有价值的相关系数
针对X、Y属于正态分布的数据:Pearson相关系数:ρxy=cov(X,Y)/二者方差之积。
Pearson相关性分析适用于服从正态分布的两定量变量,若两变量通过绘制散点图后发现存在线性趋势,可以通过计算Pearson相关系数来描述两变量的线性相关性。
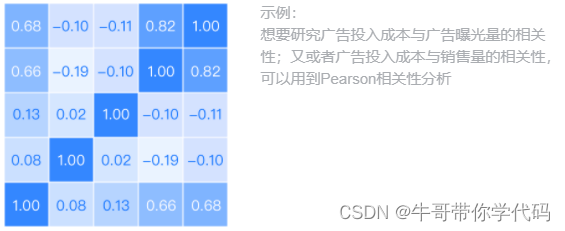
输入输出描述
输入:两个或者两个以上的定量变量。
输出:两两变量之间是否呈现显著性相似以及相似的程度
针对X、Y属于非正态分布的数据:SPearman相关系数
Spearman相关系数适用于定量变量或定序变量两两之间的相关分析,利用两变量的秩次大小作线性相关分析,对原始变量的分布不作要求,当我们变量中至少存在一个有序变量时,可使用Spearman系数来描述两变量的相关性。对于均为定量数据亦可计算Spearman相关系数,但统计效能要低一些。
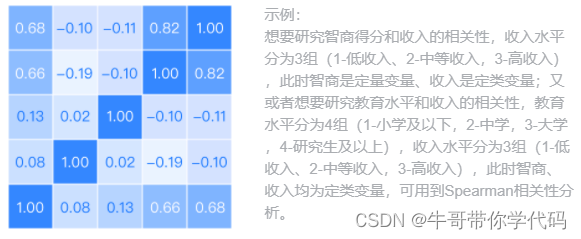
输入:两个或者两个以上的定量变量或有序定类变量(有序定类变量可用数值代替)。
输出:两两变量之间是否呈现显著性相似以及相似的程度。
Pearson相关系数(适用于定量数据,且数据满足正态分布)
Spearman相关系数(数据不满足正态分布时使用)
Kendall's tau-b等级相关系数数据为有序的定类变量
Person相关系数:反映线性相关的强弱,其中当变量为多个时,使用Pearson相关系数矩阵。
几个重要的概念
方差分析:检验试验中有关因素对实验结果的影响的显著性。
试验指标:衡量或考核实验结果的参数
因素:影响试验指标的条件
水平:因素的不同状态或内容。
逐步回归:设计多元回归时,使用该方法可以筛选变量
截距模型:将所有自变量删除后只剩下一个截距系数的模型。例如:y=h,后续可以通过改变后面的自变量,观察其他模型的因变量与截距模型中因变量的差异来判断自变量对因变量的影响强弱。
典型相关分析:检查两组变量之间的相关关系。



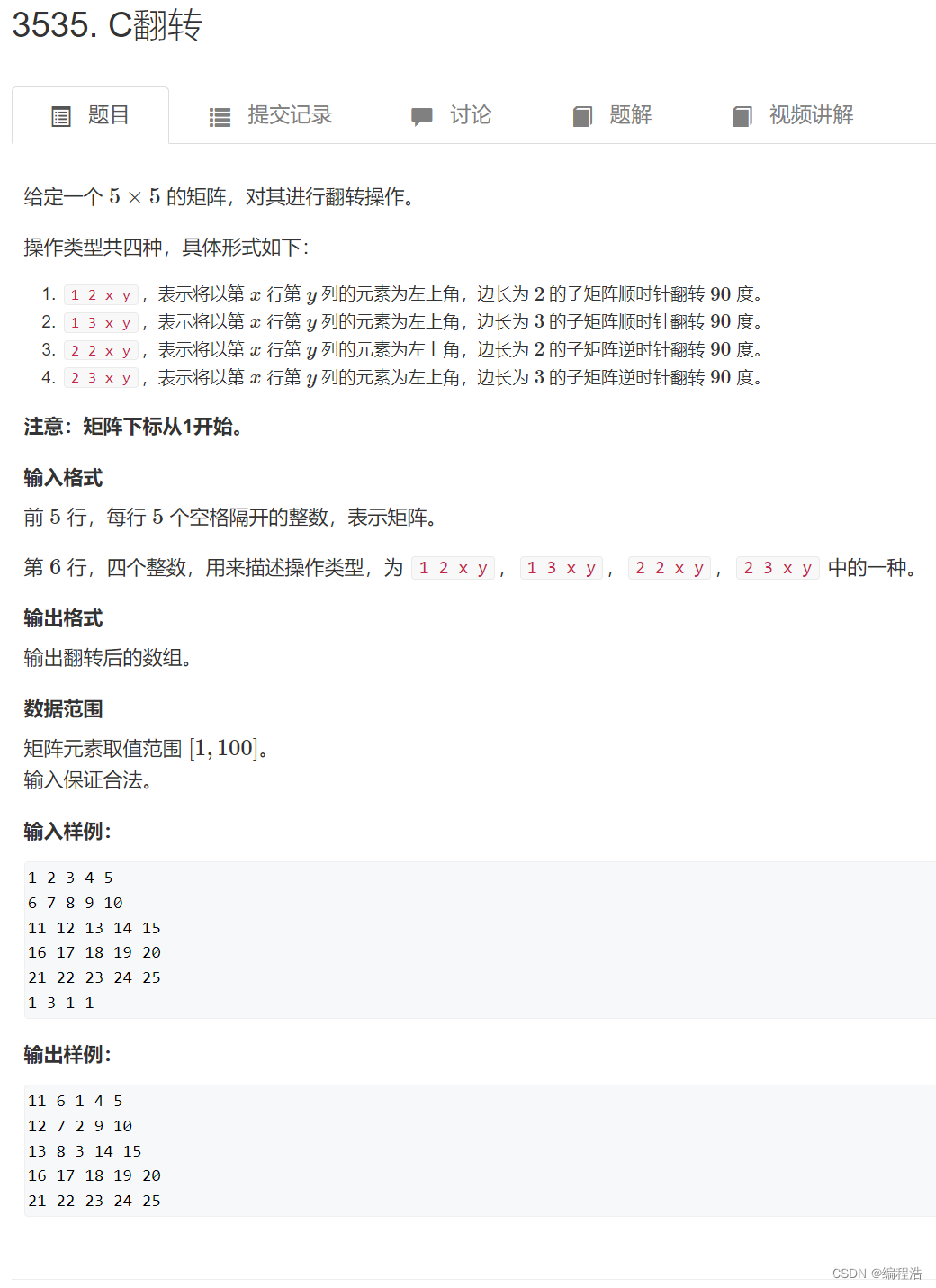




![[数据集][目标检测]遛狗不牵绳数据集VOC格式-1980张](https://i0.hdslb.com/bfs/archive/b218ed1884b250be57b2ee3ae09d26814eb427c8.jpg@100w_100h_1c.png@57w_57h_1c.png)