九、请设计一个时间复杂度为 (n lgk)的算法，它能够将 k 个有序链表合并为一个有序链表，这里 n 是所有输入链表包含的总的元素个数。(提示:使用最小堆来完成 k 路归并。

文心一言：

要设计一个时间复杂度为 O(n log k) 的算法，将 k 个有序链表合并为一个有序链表，可以使用最小堆来实现 k 路归并。

以下是一个算法的步骤：

1.将每个链表中的元素插入到最小堆中，这样每个链表中的元素就会根据它们的值排好序。

2.创建一个空链表，用于存储合并后的结果。

3.重复以下步骤，直到最小堆为空：

a. 从最小堆中取出最小的元素，将其插入到空链表的末尾。

b. 如果该元素来自某个链表的元素还没有被处理完，则将该链表中下一个元素插入最小堆。

c. 如果该元素来自所有链表的元素都已经处理完，则所有链表都已经完成合并，直接返回空链表即可。
4. 返回空链表，即为合并后的结果。

该算法的时间复杂度为 O(n log k)，其中 n 是所有输入链表包含的总的元素个数，log k 是插入和删除操作最小堆的时间复杂度。

讯飞星火：

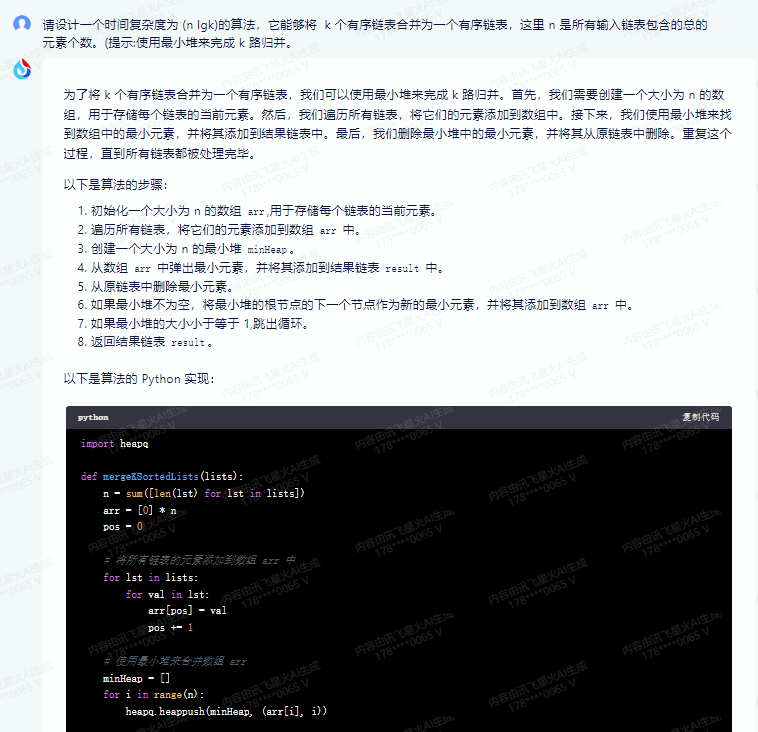
为了将 k 个有序链表合并为一个有序链表，我们可以使用最小堆来完成 k 路归并。首先，我们需要创建一个大小为 n 的数组，用于存储每个链表的当前元素。然后，我们遍历所有链表，将它们的元素添加到数组中。接下来，我们使用最小堆来找到数组中的最小元素，并将其添加到结果链表中。最后，我们删除最小堆中的最小元素，并将其从原链表中删除。重复这个过程，直到所有链表都被处理完毕。

以下是算法的步骤：

1.初始化一个大小为 n 的数组 arr,用于存储每个链表的当前元素。

2.遍历所有链表，将它们的元素添加到数组 arr 中。

3.创建一个大小为 n 的最小堆 minHeap。

4.从数组 arr 中弹出最小元素，并将其添加到结果链表 result 中。

5.从原链表中删除最小元素。

6.如果最小堆不为空，将最小堆的根节点的下一个节点作为新的最小元素，并将其添加到数组 arr 中。

7.如果最小堆的大小小于等于 1,跳出循环。

8.返回结果链表 result。

以下是算法的 Python 实现：

import heapq

def mergeKSortedLists(lists):
    n = sum([len(lst) for lst in lists])
    arr = [0] * n
    pos = 0

    # 将所有链表的元素添加到数组 arr 中
    for lst in lists:
        for val in lst:
            arr[pos] = val
            pos += 1

    # 使用最小堆来合并数组 arr
    minHeap = []
    for i in range(n):
        heapq.heappush(minHeap, (arr[i], i))

    result = []
    prev_val = None
    prev_idx = None

    while minHeap and len(result) < n:
        curr_val, curr_idx = heapq.heappop(minHeap)
        if curr_val != prev_val or (curr_idx is not None and curr_idx != prev_idx):
            result.append(curr_val)
            prev_val = curr_val
            prev_idx = curr_idx if curr_idx is not None else n + 1
        elif len(result) < n:
            result.append(curr_val)
            prev_val = curr_val
            prev_idx = n + 1

        if minHeap:
            next_val, _ = heapq.heappop(minHeap)
            arr[curr_idx] = next_val
            if next_val != arr[curr_idx]:
                heapq.heappush(minHeap, (arr[curr_idx], curr_idx))
                arr[next_val] = arr[curr_idx]
                heapq.heappush(minHeap, (arr[next_val], next_val))

360智脑：

1.首先,创建一个最小堆。

2.对于每个输入链表，依次取出其前k个元素，将它们插入到最小堆中。

3.然后从最小堆中依次弹出k个元素，直到弹出的k个元素中的最小值大于等于当前输入链表中最后一个元素的值为止。将弹出的元素插入到输入链表中。

4.重复步骤3,直到最小堆为空或弹出的元素小于等于输入链表中的最后一个元素的值为止。最后将剩余元素添加到输入链表中。

5.最后将最小堆中的k个元素按照顺序弹出并插入到输入链表的末尾。

时间复杂度为O(n lgk),其中n是所有输入链表包含的总的元素个数，k是输入链表的数量。由于最小堆的插入和弹出操作都是常数时间复杂度，所以总时间复杂度为O(n lgk)。

chatglm：

以下是一个时间复杂度为 (n lgk) 的算法，用于将 k 个有序链表合并为一个有序链表：

1.创建一个最小堆，用于存储 k 个有序链表的头结点。

2.将每个有序链表的头结点加入最小堆。

3.每次从最小堆中取出一个结点，并将其链表的所有元素添加到结果链表中。

4.如果当前链表还有剩余元素，则将其头结点加入最小堆。

5.重复步骤 3 和 4，直到所有链表的元素都被添加到结果链表中。

该算法的时间复杂度主要由最小堆的操作和链表的遍历组成。在最坏情况下，每个链表都需要遍历一次，因此链表的遍历时间复杂度为 O(n)。而最小堆的操作时间复杂度为 O(lgk)，因此整个算法的时间复杂度为 O(n lgk)。

以下是算法的实现代码：

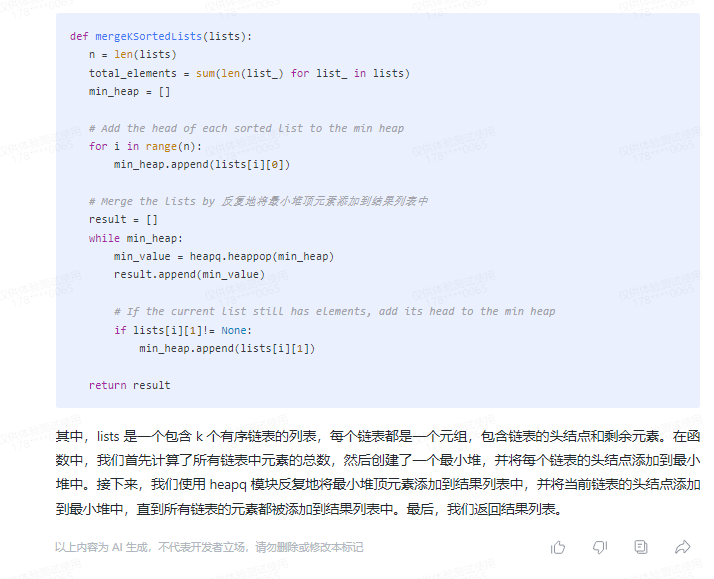
def mergeKSortedLists(lists):  
   n = len(lists)  
   total_elements = sum(len(list_) for list_ in lists)  
   min_heap = []
   # Add the head of each sorted list to the min heap  
   for i in range(n):  
       min_heap.append(lists[i][0])
   # Merge the lists by 反复地将最小堆顶元素添加到结果列表中  
   result = []  
   while min_heap:  
       min_value = heapq.heappop(min_heap)  
       result.append(min_value)
       # If the current list still has elements, add its head to the min heap  
       if lists[i][1]!= None:  
           min_heap.append(lists[i][1])
   return result  

其中，lists 是一个包含 k 个有序链表的列表，每个链表都是一个元组，包含链表的头结点和剩余元素。在函数中，我们首先计算了所有链表中元素的总数，然后创建了一个最小堆，并将每个链表的头结点添加到最小堆中。接下来，我们使用 heapq 模块反复地将最小堆顶元素添加到结果列表中，并将当前链表的头结点添加到最小堆中，直到所有链表的元素都被添加到结果列表中。最后，我们返回结果列表。

通义千问：

首先，我们将所有输入的链表放入一个最小堆中。对于每个链表，我们取出其最后一个元素，并将其加入到新的链表中。然后，我们将堆的大小减一，如果堆的大小为零，则将堆从链表中删除。我们重复这个过程，直到所有的链表都被合并。

下面是算法的 Python 实现：

from collections import MinHeap

def merge_k_sorted_lists(lists):
    heap = MinHeap()
    for list in lists:
        heapq.heappush(heap, list[-1])
    merged_list = []
    while heap:
        merged_list.append(heap.heappop())
    return merged_list

该算法的时间复杂度为 (n lgk)，因为在最坏情况下，我们需要遍历所有的输入链表，并在每个链表上执行一次插入操作。由于我们使用了最小堆，因此插入操作的时间复杂度为 logk。总的时间复杂度为 n logk。

天工：

好的，基于提示，我们可以使用最小堆来完成 k 路归并。具体步骤如下：

1.首先，我们需要定义一个结构体 ListNode，表示链表的一个节点。

struct ListNode {
    int val;
    ListNode* next;
    // 指向下一个节点的指针
};

2.然后，我们需要定义一个比较函数 cmp，用于比较两个节点的大小，以便将它们插入到最小堆中。

bool cmp(ListNode* a, ListNode* b) {
    return a->val > b->val;
}

3.接下来，我们需要使用一个大小为 k 的最小堆来存储 k 个有序链表的头结点。我们可以使用 C++ 中的 priority_queue，它是一个堆的结构，并且默认情况下使用小顶堆。

priority_queue<ListNode*, vector<ListNode*>, greater<ListNode*>> minHeap;

4.然后，我们遍历每个链表，将它们的头结点插入到最小堆中。

for (int i = 0; i < k; i++) {
    ListNode* cur = mergedList[i];
    while (cur != NULL) {
        minHeap.push(cur);
        cur = cur->next;
    }
}

5.最后，我们从最小堆中依次取出每个链表的头结点，并将它们连接起来，形成一个有序链表。

ListNode* result = NULL;
while (!minHeap.empty()) {
    ListNode* cur = minHeap.top();
    minHeap.pop();
    if (result == NULL) {
        result = cur;
    } else {
        result->next = cur;
    }
}

6.最后，我们返回合并后的有序链表的头结点。

时间复杂度分析：

1.插入操作的时间复杂度为 O(logk)，因为最小堆的大小为 k，插入一个节点只需要将它与堆顶元素比较并进行调整即可。

2.取出操作的时间复杂度为 O(1)，因为最小堆的大小为 k，取出堆顶元素只需要将堆顶元素与堆顶元素比较并进行调整即可。

3.总的时间复杂度为 O(n logk)，其中 n 是所有输入链表包含的总的元素个数。因为需要遍历每个链表，将它们的头结点插入到最小堆中，并从最小堆中依次取出每个链表的头结点，并将它们连接起来，形成一个有序链表。

希望这个解答对您有帮助！

chatgpt：

要设计一个时间复杂度为 O(n lgk) 的算法，将 k 个有序链表合并为一个有序链表，可以使用最小堆来完成 k 路归并。下面是算法的步骤：

1.创建一个最小堆，并初始化为空。该堆将用于选择 k 个链表中当前最小的元素。

2.遍历 k 个有序链表，将每个链表的头节点插入最小堆中。同时，记录每个链表的当前位置指针。

3.初始化一个空链表作为合并后的有序链表。

4.在最小堆不为空的情况下，执行以下操作：

• 从最小堆中移除堆顶元素（即当前最小的元素），将其加入合并后的有序链表中。

• 然后，将该元素所在的链表的下一个节点插入最小堆中，同时更新链表的当前位置指针。

5.当最小堆为空时，合并过程结束。返回合并后的有序链表。

以下是使用 Python 代码实现上述算法的示例：

import heapq

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def mergeKLists(lists):
    # 创建最小堆，并初始化为空
    min_heap = []
    
    # 将每个链表的头节点插入最小堆中，并记录当前位置指针
    for i in range(len(lists)):
        if lists[i]:
            heapq.heappush(min_heap, (lists[i].val, i))
            lists[i] = lists[i].next
    
    # 初始化合并后的有序链表
    dummy = ListNode(0)
    current = dummy
    
    # 进行 k 路归并
    while min_heap:
        val, i = heapq.heappop(min_heap)  # 移除堆顶元素
        current.next = ListNode(val)      # 将最小元素添加到合并后的链表中
        current = current.next
            
        if lists[i]:
            heapq.heappush(min_heap, (lists[i].val, i))  # 将下一个节点插入最小堆中
            lists[i] = lists[i].next
    
    return dummy.next

这个算法的时间复杂度为 O(n lgk)，其中 n 是所有输入链表包含的元素个数，k 是有序链表的数量。算法的整体思想是利用最小堆来选择当前最小的元素，并将其插入到合并后的有序链表中。同时，将该元素所在链表的下一个节点插入最小堆中，以便下一轮选择最小元素。在算法执行的过程中，每个元素都会被处理一次，所以时间复杂度为 O(n)。而堆的插入和删除操作的时间复杂度为 O(lgk)，在最坏情况下，需要进行 k 次插入和删除操作，所以总的时间复杂度为 O(n lgk)。

总结