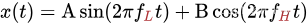
一、思路

BFS

二、解题方法

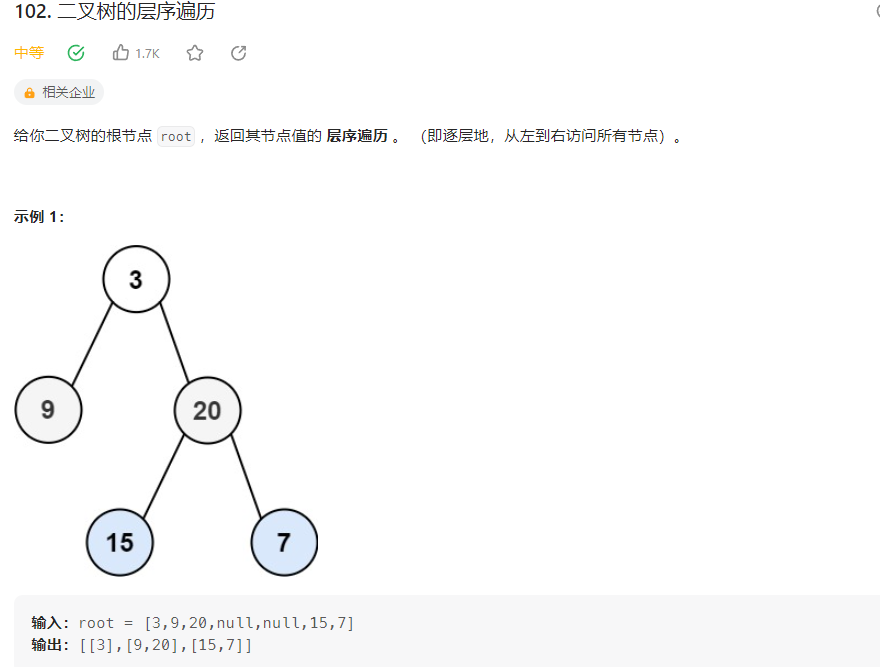
通过广度优先搜索（BFS）的方式，按层遍历二叉树节点，并将每层的节点值保存在一个一维数组中，然后再将所有的一维数组存储在二维数组中，最后返回二维数组作为层序遍历的结果。

三、code

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector <vector <int>> ret;//定义一个二维数组 ret，用于存储层序遍历的结果。
        //如果输入的二叉树根节点为空，直接返回空的结果数组 ret。
        if (!root) {
            return ret;
        }

        queue <TreeNode*> q;//定义一个队列 q，用于辅助进行广度优先搜索（BFS）
        q.push(root);//将根节点入队，表示从根节点开始进行遍历。
        while (!q.empty()) {//当队列 q 不为空时，执行循环体内的操作。
            int currentLevelSize = q.size();//获取当前队列的大小，表示当前层的节点数。
            ret.push_back(vector <int> ());//在结果数组 ret 中添加一个空的一维数组，用于存储当前层的节点值。
            for (int i = 1; i <= currentLevelSize; ++i) {//循环处理当前层的节点。
                auto node = q.front(); q.pop();//获取当前队列的头节点，并将其出队。
                ret.back().push_back(node->val);//将当前节点的值加入到结果数组 ret 的最后一个一维数组中，即当前层的节点值数组。
                if (node->left) q.push(node->left);//如果当前节点有左子节点，将左子节点入队，继续遍历左子树。
                if (node->right) q.push(node->right);// 如果当前节点有右子节点，将右子节点入队，继续遍历右子树。
            }
        }
        
        return ret;
    }
};

=========================================================================学到的知识：

BFS（广度优先搜索）和DFS（深度优先搜索）是两种常见的图和树遍历算法，它们在搜索问题中有不同的应用和特点。

BFS（广度优先搜索）：

1. BFS是一种层序遍历算法，从起始节点开始，逐层遍历节点。
2. 使用队列数据结构来实现，首先将起始节点入队，然后每次从队列中取出一个节点进行处理，并将其邻居节点入队。
3. 由于BFS是逐层遍历，因此可以用于寻找最短路径和最小步数等问题。
4. BFS通常适用于树或图中需要按层遍历节点的情况。

DFS（深度优先搜索）：

1. DFS是一种先序遍历算法，从起始节点开始，沿着一条路径尽可能深入，直到到达最深的节点，然后回溯，再选择其他路径。
2. 使用栈数据结构（或递归）来实现，首先将起始节点入栈，然后每次从栈中取出一个节点进行处理，并将其邻居节点入栈。
3. DFS不逐层遍历，可能会在树或图中深入到较远的节点，因此适用于一些搜索路径的问题，如寻找所有可能的路径或找到特定路径的问题。
4. DFS也可能陷入无限循环，因此在使用时需要注意避免死循环。