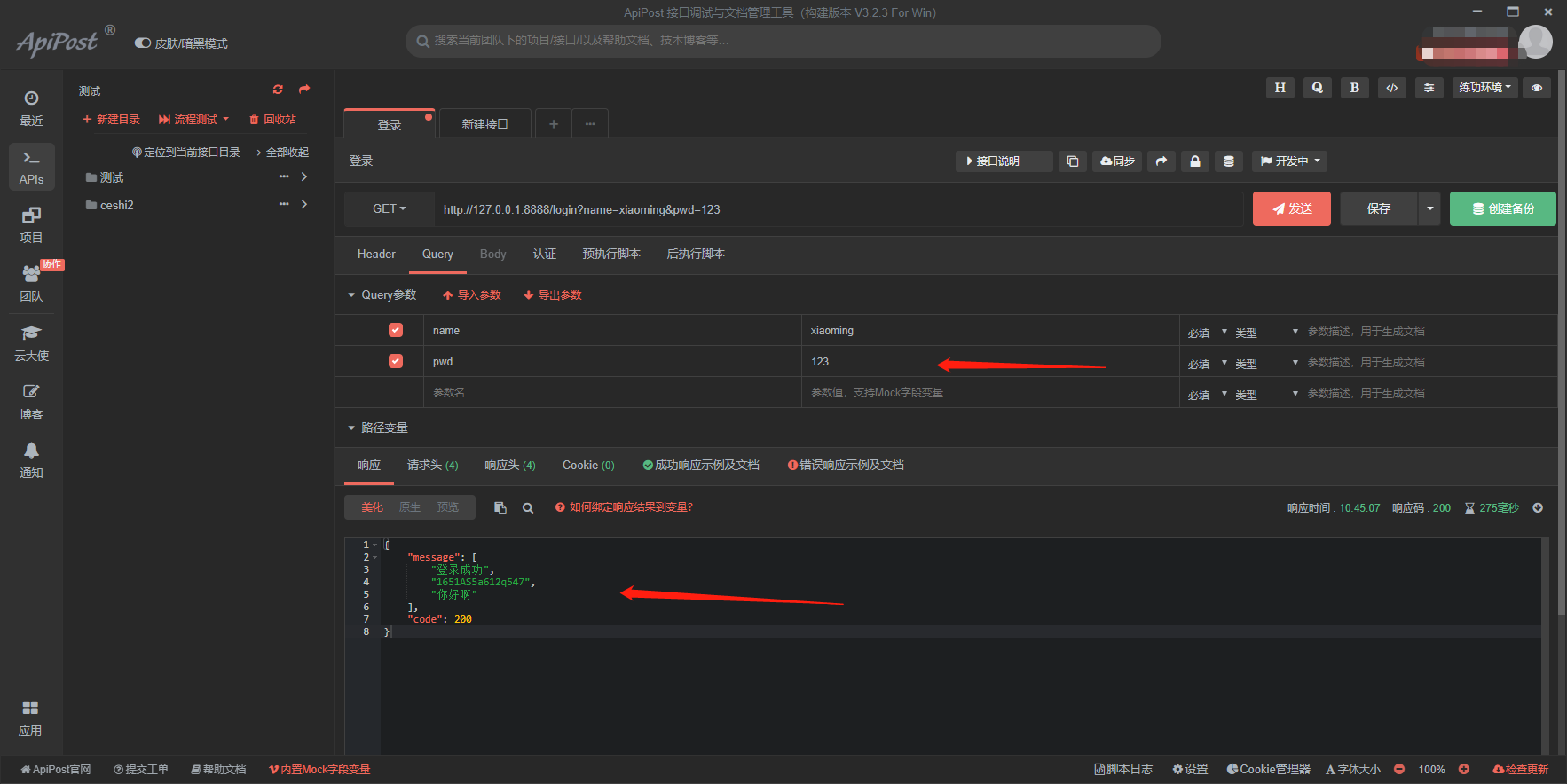
1. 前序中序后序递归写法

前序

public void preorder(TreeNode root, List<Integer> res) {
        if (root == null) {
            return;
        }
        res.add(root.val);
        preorder(root.left, res);
        preorder(root.right, res);
    }

后序

public static void postOrderRecur(TreeNode head) {
    if (head == null) {
        return;
    }
    postOrderRecur(head.left);
    postOrderRecur(head.right);
    System.out.print(head.value + " ");
}

中序

public static void inOrderRecur(TreeNode head) {
    if (head == null) {
        return;
    }
    inOrderRecur(head.left);
    System.out.print(head.value + " ");
    inOrderRecur(head.right);
}

2. 前序遍历迭代法

前序遍历的主要特征是中左右
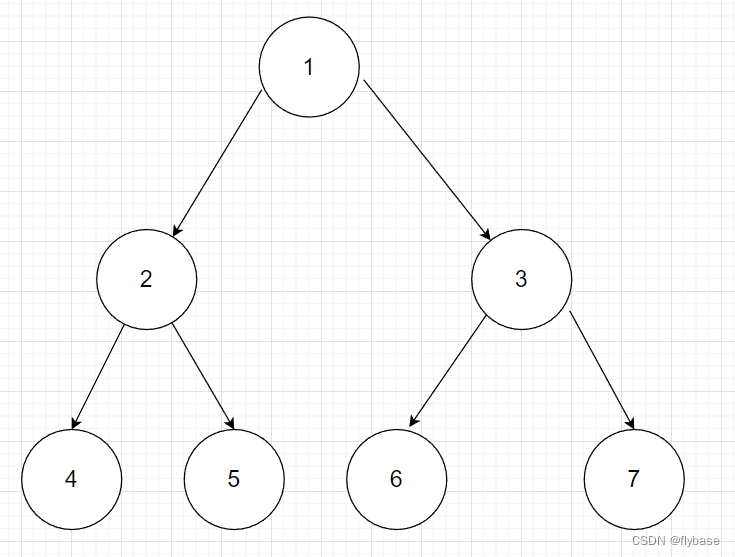
在这里插入图片描述
上面的前序遍历是：1 2 4 5 3 6 7
很明显 1 2 4都是左子树，然后遍历完了才到右子树，那么迭代需要做的就是一直遍历左子树节点，然后保存当前的左子树的根节点，左子树完了，然后去除节点找到右节点。这里面需要使用栈来进行存储节点，然后按照相应的顺序弹出节点。

2.1 二叉树的前序遍历

二叉树的前序遍历
给你二叉树的根节点 root ，返回它节点值的前序遍历。
输入：root = [1,null,2,3]
输出：[1,2,3]
在这里插入图片描述

 public List<Integer> preorderTraversal(TreeNode root) {
      List<Integer> res = new ArrayList<>();
      if(root == null)  return res;
      Deque<TreeNode> stack = new LinkedList<>();
      TreeNode node = root;
      while(!stack.isEmpty() || node!=null){
          while(node!=null){
              res.add(node.val);
              // 保存根节点，找到对应的右节点
              stack.push(node);
              // 处理左子树
              node = node.left;
          }
          // 找到对应的右节点的根节点
        node = stack.pop();
        // 处理右子树
        node=node.right;
      }
      return res;
    }

3. 迭代法中序遍历

特点：左中右
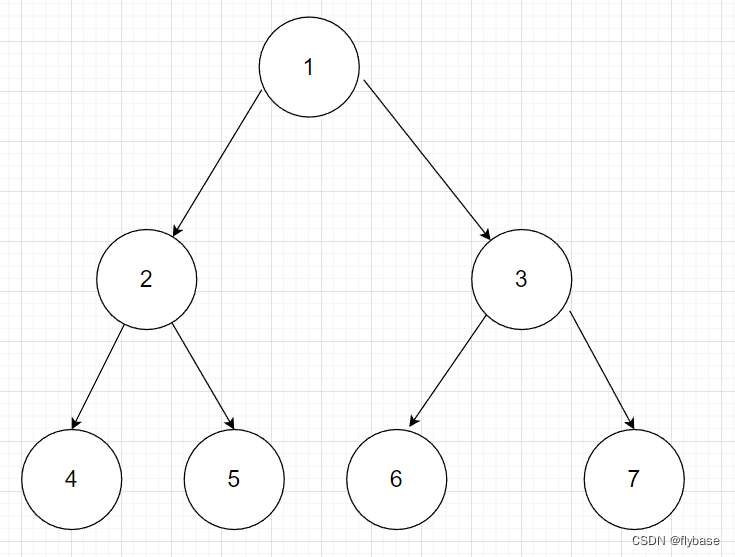
在这里插入图片描述
元素：4 2 5 1 6 3 7
这个可以看作每次先遍历最左的子树节点，然后输出最下面的节点，逆序，如果根节点还有右节点，就继续进入右节点到最下面，否则依然逆序输出。依然需要使用一个栈来存储这个节点。

3.1 二叉树的中序遍历

二叉树的中序遍历
给定一个二叉树的根节点 root ，返回它的中序遍历。

输入：root = [1,null,2,3]
输出：[1,3,2]

总体上一致，只不过添加的时候是添加的当前链路最后一个节点元素。

    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root ==null) return res;
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        while(!stack.isEmpty() || node!=null){
            while(node!=null){
                stack.push(node);
                node=node.left;
            }
            // 此时已经到头了
            node = stack.pop();
            res.add(node.val);
            node=node.right;
        }
        return res;
    }

4. 后序遍历

特点：左右中
在这里插入图片描述
元素：4 5 2 6 7 3 1
元素特点：需要输出当前根节点的两个子节点的值，然后再输出根节点。但是实际操作下来发现很麻烦，将后序便利的元素反转变成 1 3 7 6 2 5 4, 而这样就和前序类似，只不过区别在于前序先遍历左节点，现在需要遍历右节点，然后将列表元素整体反转。

4.1 二叉树的后序遍历

二叉树的后序遍历
给你一棵二叉树的根节点 root ，返回其节点值的后序遍历。

 public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null) return res;
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        while(!stack.isEmpty() || node!=null){
            while(node!=null ){
                res.add(node.val);
                stack.push(node);
                node= node.right;
            }
            node =  stack.pop();
            node = node.left;
        }
        Collections.reverse(res);
        return res;
    }

但是这个方法并没有用到相关的后序遍历的特性，只是使用的前序

4.2 迭代法

public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if(root == null) return res;
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = null;
        while(!stack.isEmpty() || root!=null){
            while(root!=null ){
                stack.push(root);
                root= root.left;
            }
            root =  stack.pop();
            // 如果右子树为空或者已经被访问过了，才能添加当前节点值
            if(root.right==null || root.right == node){
                res.add(root.val);
                node=root;
                root=null;
            }else{
                stack.push(root);
                root = root.right;
            }
        }
        return res;
    }