pcl协方差计算精度

news2024/11/16 18:05:38

最近在计算法线的时候发现法线的结果偏差很大，经过分析得到在计算点云协方差矩阵时，选择不同的方法会导致不同的结果。下面是测试过程：
1、测试点云

点云是中间一点的邻域点，是从上往下看，法线的方向近似为（0，0，1）也就是沿着Z轴方向。

第一种方法：按照公式计算

1、先计算中心点

pcl::compute3DCentroid(*cloud, centroid);
 4.26244
-9.52218
 7.24367
       1

2、计算去中心化的点云

pcl::demeanPointCloud(*cloud, centroid, cloud_demean);

3、计算协方差矩阵

covariance_matrix = static_cast<Eigen::Matrix3f> (cloud_demean.topRows<3>() * cloud_demean.topRows<3>().transpose());
    1.56941  0.00116825  0.00467487
 0.00116825     1.57477  0.00205587
 0.00467487  0.00205587 0.000789469

4、特征向量

Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> evd(covariance_matrix);
0.000772649
    1.56918
    1.57502
-0.00297917   -0.978679    0.205372
 -0.0013039    0.205377    0.978682
   0.999995 -0.00264787  0.00188798

注：以上的协方差矩阵并没有除以数据的个数n，下面为除以n的结果

covariance_matrix /= cloud->size();
 0.00039853  2.9666e-07 1.18712e-06
 2.9666e-07 0.000399891 5.22061e-07
1.18712e-06 5.22061e-07 2.00475e-07

相应的特征值和特征向量

evd.compute(covariance_matrix);
1.96266e-07
0.000398471
0.000399955
-0.00297925    -0.97868    0.205369
-0.00130392    0.205373    0.978683
   0.999995 -0.00264789  0.00188795

可以看出两者获取的特征向量是相同的，由于计算误差的问题，导致小数点后四五位后有差异，可以接受。

第二种方法：对公式进行化简

计算代码如下：

		for (size_t i = 0; i < point_count; ++i)
		{
			accu[0] += cloud[i].x * cloud[i].x;
			accu[1] += cloud[i].x * cloud[i].y;
			accu[2] += cloud[i].x * cloud[i].z;
			accu[3] += cloud[i].y * cloud[i].y; // 4
			accu[4] += cloud[i].y * cloud[i].z; // 5
			accu[5] += cloud[i].z * cloud[i].z; // 8
			accu[6] += cloud[i].x;
			accu[7] += cloud[i].y;
			accu[8] += cloud[i].z;
		}
				centroid[0] = accu[6]; centroid[1] = accu[7]; centroid[2] = accu[8];
		centroid[3] = 1;
		covariance_matrix.coeffRef(0) = accu[0] - accu[6] * accu[6];
		covariance_matrix.coeffRef(1) = accu[1] - accu[6] * accu[7];
		covariance_matrix.coeffRef(2) = accu[2] - accu[6] * accu[8];
		covariance_matrix.coeffRef(4) = accu[3] - accu[7] * accu[7];
		covariance_matrix.coeffRef(5) = accu[4] - accu[7] * accu[8];
		covariance_matrix.coeffRef(8) = accu[5] - accu[8] * accu[8];
		covariance_matrix.coeffRef(3) = covariance_matrix.coeff(1);
		covariance_matrix.coeffRef(6) = covariance_matrix.coeff(2);
		covariance_matrix.coeffRef(7) = covariance_matrix.coeff(5);

可以确定这里的计算方法是没有问题的。根据公式可以得到，此方法计算得到的是除以数据n的结果

pcl::computeMeanAndCovarianceMatrix(*cloud, covariance_matrix1, centroid1);
 0.000402451  6.10352e-05 -0.000331879
 6.10352e-05  9.91821e-05  0.000862122
-0.000331879  0.000862122  -0.00104523

计算特征值和特征向量

Eigen::SelfAdjointEigenSolver<Eigen::Matrix3f> evd1(covariance_matrix1);
-0.00156048
0.000393528
0.000623361
 0.161933  0.843809  0.511628
-0.459571    0.5233 -0.717601
 0.873254  0.118926  -0.47253

从以上结果可以看出，这里的结果明显是有问题的，对称矩阵的特征值都是正的。
下面将数据换成double类型进行测试：

Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d> evd1(covariance_matrix1);
协方差：
0.000398508 2.87849e-07   1.166e-06
2.87849e-07 0.000399546 4.86634e-07
  1.166e-06 4.86634e-07 4.04394e-08
特征值：
3.64367e-08
0.000398436
0.000399622
特征向量：
0.00292528    0.96767   0.252203
0.00121596  -0.252208   0.967672
 -0.999995 0.00252404 0.00191443

可以看出，以上结果是正确的。

总结：

分析产生以上结果的原因：float类型在计算平方时，由于有效数字较少，当平方很大时，小数点后面的部分就被忽略，造成除以n之后的结果变得精度不够。
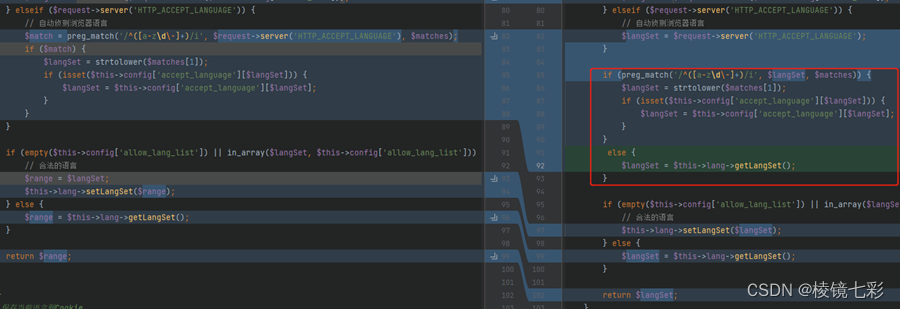
逐步对比float和double两个类型的计算结果

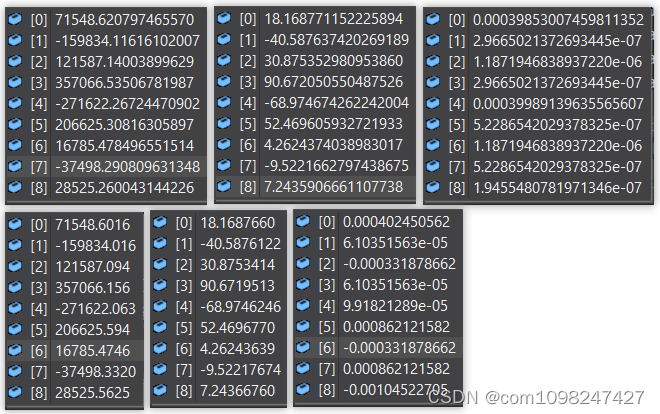
上侧为double，下侧为float
之所以产生这样的结果，是由于未中心化的点云数据坐标值较大，直接进行平方运算数值就会变得很大，由于float的有效数字9位，
4.26249981的平方，
double计算结果：18.168904623985327
float计算结果：18.1689053
这些一点点的差异最终就会造成结果造成很大的误差。
由于方法一只有一次乘法，相对而言计算结果会好点。

pcl协方差计算中有介绍

  /** \brief Compute the normalized 3x3 covariance matrix and the centroid of a given set of points in a single loop.
    * Normalized means that every entry has been divided by the number of entries in indices.
    * For small number of points, or if you want explicitely the sample-variance, scale the covariance matrix
    * with n / (n-1), where n is the number of points used to calculate the covariance matrix and is returned by this function.
    * \note ***This method is theoretically exact. However using float for internal calculations reduces the accuracy but increases the efficiency.***
    * \param[in] cloud the input point cloud
    * \param[out] covariance_matrix the resultant 3x3 covariance matrix
    * \param[out] centroid the centroid of the set of points in the cloud
    * \return number of valid point used to determine the covariance matrix.
    * In case of dense point clouds, this is the same as the size of input cloud.
    * \ingroup common
    */

其中说明了：这个方法理论上是准确的。然而，使用浮点数进行内部计算降低了精度，但提高了效率。

注意：PCL法线估计方法，使用的就是方法二，导致计算结果偏差很大。怎么改进呢？
修改如下代码：

		inline bool
			computePointNormal(const pcl::PointCloud<PointInT> &cloud, const std::vector<int> &indices,
				float &nx, float &ny, float &nz, float &curvature)
		{
			
			if (indices.size() < 3 ||
				compute3DCentroid(cloud, indices, xyz_centroid_) == 0||
				computeCovarianceMatrix(cloud, indices, xyz_centroid_, covariance_matrix_)==0)
			{				
				nx = ny = nz = curvature = std::numeric_limits<float>::quiet_NaN();
				return false;				
			}

			// Get the plane normal and surface curvature
			solvePlaneParameters(covariance_matrix_, nx, ny, nz, curvature);
			return true;
		}