总结
近几期的题目质量有所提升,数据范围还是一如既往的没给。对于算法题,给定详细的数据范围,规范输入输出,再多给出几个样例以及样例说明,参赛的体验感才会提升。
题目列表
1.小球游戏
题目描述
某台有10个小球的游戏机,其设定的规则如下: 每一轮游戏在开始之前会把编号为0到9的小球依次放入从左到右编号也为0到9的10个位置;游戏开始后会快速对调任意 两个球的位置若干次,并在结束时要求观众写出从左到右的小球编号顺序,写对就得奖。 由于速度很快,所以直接靠观看写对很难。但有个程序员发现这台游戏机其实有一个固定的长度为n的操作序列数据库, 每一轮游戏都是随机取一个起始操作序列编号和一个结束操作序列编号(操作序列编号从1到n)并从起始到结束依次执行 每个操作序列编号对应的操作,而每个操作序列编号对应的操作就是对该次操作指定的两个编号的位置上的小球进行对 调。 现在给出操作序列数据库和每一轮游戏的起始操作序列编号和结束操作序列编号,求每轮游戏结束时从左到右的小球编号 顺序。
分析
前几期才考过的题目,但是貌似没有写过题解。题目比较长但是意思还是很简单的,按照题意直接模拟游戏操作,每轮游戏根据操作序列对原始序列对应位置上的小球进行交换即可。
代码
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 100005;
pair<int,int> q[N];
int main() {
int n,m;
cin>>n>>m;
for(int i = 1; i <= n; i++) cin>>q[i].first>>q[i].second;
int c,d;
vector<int> p(10, 0);
for(int i = 0; i < 10; i++) p[i] = i;
while(m--) {
vector<int> t = p;
cin>>c>>d;
for(int i = c; i <= d; i++) {
swap(t[q[i].first], t[q[i].second]);
}
for (int i = 0; i < 10; i++) cout<<t[i]<<" \n"[i==9];
}
return 0;
}
2.王子闯闸门
题目描述
波斯王子要去救被贾法尔囚禁的公主,但贾法尔用黑魔法在他面前设置了编号从1到n的n道闸门。从王子的位置到1号闸门 需要1秒,从n号闸门到公主所在的位置也需要1秒,从p号闸门到p+1或p-1号闸门都需要1秒。 每过1秒钟,王子都必须 决定选择前进一道闸门、后退一道闸门或停在原地这三种动作中的一种。当然,王子不能选择移动到关闭状态的闸门而只 能选择开启状态的闸门。在王子做出动作选择后,闸门也可能会有关闭和开启的动作,如果王子做完动作后,其所在的闸 门在该秒内的动作是从开启变为关闭则他就会被闸门夹死。 现在给出闸门数量n和m个闸门的动作时刻表,求波斯王子需 要多少秒才能救出公主。
分析
题目不错,唯一的诟病是不给数据范围,对于这种与数据范围强相关的题目,没有数据范围去求解,只能不断的尝试了。
状态由时间和位置两个维度组成,可以用下面的图来表示。
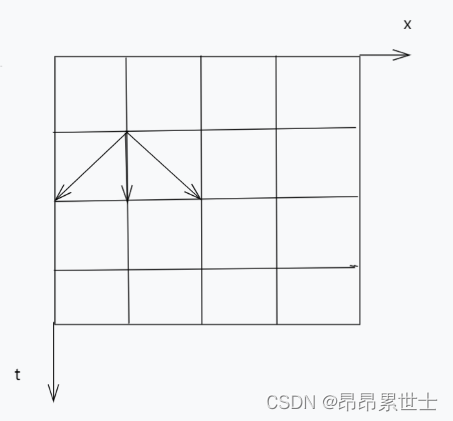
( t , x ) (t,x) (t,x)表示第 t t t秒在 x x x位置的状态,如图所示, ( 1 , 1 ) (1,1) (1,1)可以转移到 ( 2 , 0 ) (2,0) (2,0)、 ( 2 , 1 ) (2,1) (2,1)和 ( 2 , 2 ) (2,2) (2,2)三种状态。也可以说, ( t , x ) (t,x) (t,x)可以由 ( t − 1 , x − 1 ) (t-1,x-1) (t−1,x−1)、 ( t − 1 , x ) (t-1,x) (t−1,x)和 ( t − 1 , x + 1 ) (t-1,x+1) (t−1,x+1)三种状态转移而来。
状态表示: f [ i ] [ j ] f[i][j] f[i][j]表示第 i i i秒在 j j j位置上的合法性,值为 t r u e true true表示合法, f a l s e false false表示不合法。
状态转移方程:
f
[
i
]
[
j
]
=
{
f
a
l
s
e
,
第i秒时j号闸门是关闭的
f
[
i
−
1
]
[
j
−
1
]
∣
f
[
i
−
1
]
[
j
]
∣
f
[
i
−
1
]
[
j
+
1
]
,
第i秒时j号闸门是开启的
f[i][j]= \begin{cases} false, & \text{第i秒时j号闸门是关闭的}\\ \\ f[i-1][j-1]\ |\ f[i-1][j]\ |\ f[i-1][j+1],& \text{第i秒时j号闸门是开启的} \end{cases}
f[i][j]=⎩
⎨
⎧false,f[i−1][j−1] ∣ f[i−1][j] ∣ f[i−1][j+1],第i秒时j号闸门是关闭的第i秒时j号闸门是开启的
可以发现,每层状态仅与上一层的状态有关,所以可以使用滚动数组表示,即只保存两层的状态,这样可以节省空间。
使用DP求解本题的代码如下:
f[0][0] = f[1][0] = true;
for (int i = 1; i < N;i++) {
int t1 = i & 1, t2 = 1 - t1;
for(int j = 1; j <= n;j++){
if (!check(j, i)) {
f[t1][j] = false;
continue;
}
f[t1][j] = (f[t2][j] | f[t2][j+1] | f[t2][j-1]);
}
if (f[t1][n]) {
cout<<i + 1<<endl;
return 0;
}
}
其中状态边界就是王子的位置0,任何时间段都是合法的。考试时没有使用DP求解,上面代码可以通过简单的测例,由于不知道数据范围,所以不保证可以AC。
考试时使用了BFS进行求解,仅通过了四成用例,加上各种剪枝以及记忆化搜索后还是没有通过更多的用例,最后心累了,毁灭吧,直接交了。
首先要考虑的是如何判断某一时刻的某个位置的闸门是不是关闭的,由于时间以及位置不知道范围,直接使用map显然会TLE。这里将每个闸门的关闭时间区间放到vector里,进行排序后备用。每次需要查询该闸门在 t i ti ti时刻是不是开启的,只需要对这个由区间构成的向量进行二分查找即可,查找效率还是可观的。
由于BFS过程比较简单,不再赘述。使用过的优化操作如下:
- 优化搜索顺序,最先将+1的位置入队。
- 剪枝:当+1位置后续时刻闸门不会关闭时,果断将+1位置入队,且不再考虑原地和后退的选择。
- 记忆化搜索:当某个状态 ( t , x ) (t,x) (t,x)之前入过队的时候,不再重复入队。
说下几个优化操作的效果,优化搜索顺序在DFS中效果显著,BFS里收效甚微。看了下问哥的思路是使用DFS求解,不能说这个操作没用,只是用错了地方,要是用了深搜大概可以多通过几个测例的。
剪枝操作也很重要,当时猜想有大片连续的不会关闭的闸门,所以这种情况下一直向前走,奈何BFS的性质效果也没那么好。至于记忆化搜索,由于二元组状态比较多,使用了记忆化搜索效率反而更低了,这也是开始判断某一时刻闸门是否关闭时没用使用map的原因,代码里也就删掉了记忆化搜索的语句。
BFS求解的代码如下,由于没有评测系统,就没再继续写DFS的解法了。
代码
#include <iostream>
#include <algorithm>
#include <queue>
#include <map>
using namespace std;
const int N = 100005;
typedef pair<int,int> PII;
int n,m;
vector<PII> t[N];
queue<PII> q;
bool check(int p, int ti) {
auto &v = t[p];
int l = 0, r = v.size() - 1;
if (r < 0) return true;
while(l < r) {
int mid = (l + r) >> 1;
if(ti < v[mid].first) r = mid - 1;
else if(ti > v[mid].second) l = mid + 1;
else return false;
}
if (ti >= v[l].first && ti <= v[l].second) return false;
return true;
}
int main() {
cin>>n>>m;
int a,b,c;
for(int i = 0; i < m; i++) {
cin>>a>>b>>c;
t[a].push_back({b, c});
}
for(int i = 0; i < N; i++) {
if (t[i].size()) sort(t[i].begin(), t[i].end());
}
q.push({0, 0});
int cnt = 0;
while(q.size()) {
cnt++;
PII u = q.front();
q.pop();
int p = u.first, ti = u.second + 1;
if (cnt > 1e6) {//绕过TLE
cout<<t[n].back().second + 2<<endl;
break;
}
if (p == n) {//到达n号闸门
cout<<ti<<endl;
return 0;
}
for(int i = 1; i >= -1; i--) {
if (t[p + i].empty() || t[p + i].back().second < ti) {
q.push({p+i,ti});
break;//剪枝
}
if (check(p + i, ti)) {
q.push({p+i, ti});
}
}
}
return 0;
}
![[Python] Pylance 插件打开 Python 的类型检查](https://img-blog.csdnimg.cn/a3e7252df9c94fadbb22632af69e0cae.png)