一、说明
二、关于DQN的概念和实验
DQN(Deep Q-Network)是一种基于深度学习的强化学习算法,在游戏AI中表现优异,如AlphaGo。以下是DQN代码的详细解释:
2.1 导入库和实例化环境
import gym
import random
import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.optimizers import Adam
env = gym.make('CartPole-v0')
env.seed(0)
np.random.seed(0)
random.seed(0)
首先导入需要的库,包括gym(强化学习环境)、numpy、keras等。然后实例化CartPole-v0环境,并设置随机种子以保证结果的可重复性。
2.2 定义DQN模型
model = Sequential() model.add(Dense(24, input_dim=4, activation='relu')) model.add(Dense(24, activation='relu')) model.add(Dense(2, activation='linear')) model.compile(loss='mse', optimizer=Adam(lr=0.001))
这里使用了Dense层来构建神经网络,包括两个隐藏层和一个输出层。输入层的维度为4,即环境状态的维度。输出层有两个节点,分别对应左右两种动作。激活函数使用了ReLU。目标函数为MSE(均方误差),优化器使用了Adam。
2.3 定义经验回放和动作选择函数
from collections import deque
memory = deque(maxlen=2000)
def choose_action(state, epsilon):
if np.random.rand() <= epsilon:
return env.action_space.sample()
return np.argmax(model.predict(state))
def remember(state, action, reward, next_state, done):
memory.append((state, action, reward, next_state, done))经验回放是DQN中一个重要的概念,可以缓解样本之间的相关性,增加网络的稳定性和收敛速度。这里使用deque作为经验池,最多存储2000个元素。
动作选择函数中,epsilon代表了贪心率,即选择最优动作的概率。当随机数小于epsilon时随机选择动作,否则选择Q值最大的动作。
经验记忆函数用于将每次交互得到的状态、动作、奖励、下一个状态和终止标志存储到经验池中。
2.4 定义训练函数
def replay(batch_size, epsilon):
mini_batch = random.sample(memory, batch_size)
for state, action, reward, next_state, done in mini_batch:
if done:
target = reward
else:
target = reward + np.amax(model.predict(next_state)[0]) * gamma
target_f = model.predict(state)
target_f[0][action] = target
model.fit(state, target_f, epochs=1, verbose=0)
if epsilon > epsilon_min:
epsilon *= epsilon_decay训练函数分为两部分,经验池中随机取出一批样本(batch_size),计算目标Q值,然后使用模型更新Q值。其中,如果样本是最后一个状态,则目标Q值为奖励;否则目标Q值为奖励加上下一状态的最大Q值。gamma为折扣因子,控制奖励的衰减速度。
2.5 训练DQN
batch_size = 32
gamma = 0.95
epsilon = 1.0
epsilon_min = 0.01
epsilon_decay = 0.995
episodes = 1000
for episode in range(episodes):
state = env.reset()
state = np.reshape(state, [1, 4])
for time in range(500):
action = choose_action(state, epsilon)
next_state, reward, done, _ = env.step(action)
next_state = np.reshape(next_state, [1, 4])
remember(state, action, reward, next_state, done)
state = next_state
if done:
print("episode: {}/{}, score: {}".format(episode, episodes, time))
break
if len(memory) > batch_size:
replay(batch_size, epsilon)
最后,使用一个循环来训练模型。对于每个episode,从初始状态开始,不断交互环境,执行动作、获得奖励、观察下一个状态,并将这些信息存储到经验池中。同时根据贪心策略选择动作。当episode结束时打印结果,并使用经验回放更新模型。这个循环会执行1000次。

三、强化学习简介
强化学习是机器学习的一个子领域,它教代理如何从其动作空间中选择动作。它与环境交互,以便随着时间的推移最大化奖励。够复杂吗?让我们打破这个定义以便更好地理解。
代理:您培训的计划,目的是完成您指定的工作。
环境:代理在其中执行操作的世界。
操作: 代理所做的移动,这会导致环境更改。
奖励:对一个动作的评价,就像反馈一样。
在任何强化学习建模任务中,都必须定义这 4 个基本要素。 在我们为 Covid-19 问题定义这些元素之前,让我们首先尝试通过一个例子来理解:代理如何在环境中学习操作?

代理: 控制肢体运动的程序 环境:模拟重力和运动
定律的现实世界 动作:移动肢体 L 度 Θ
奖励:接近目的地时为正;当它掉下来时为负。
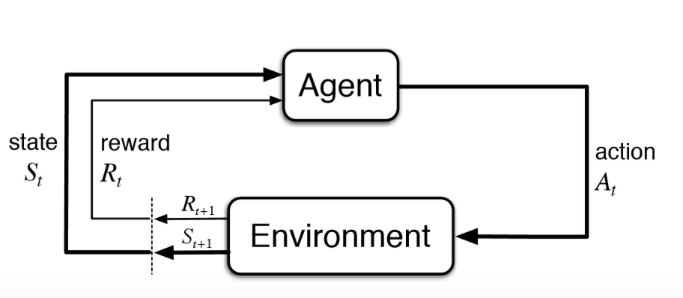
代理在交互式环境中使用来自其自身行为和经验的反馈(奖励)进行反复试验来学习。代理本质上是在环境中尝试不同的操作,并从反馈中学习它得到的回报。目标是找到一个合适的行动策略,使代理的总累积奖励最大化。
四、动作空间的问题!
但是,大多数现有的 DRL 方法要求动作空间是有限和离散的或连续的动作。
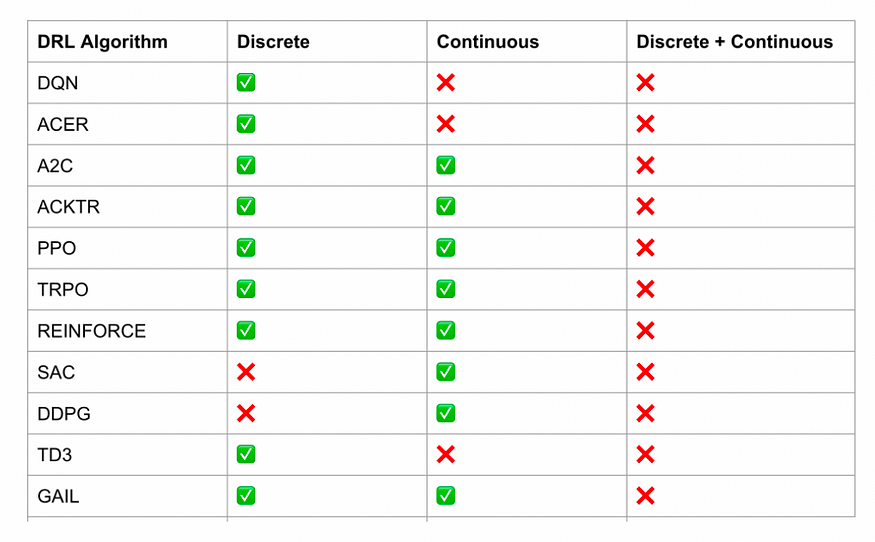
剧情 1
例如,图中呈现的算法 [1] 要么满足离散动作空间,要么满足连续动作空间。我们仍然没有一个标准的强化学习算法来处理离散-连续混合动作空间。在这篇博客中,我们将重点介绍“离散-连续混合行动空间”
五、离散-连续混合动作空间
我们已经熟悉使用连续和离散动作空间的不同环境。在我们进入可以解决混合动作空间的算法之前,快速了解离散-连续混合动作空间的外观。
我们首先从由 [k] 表示的可用离散动作 {1,2,3....K} 中选择一个高电平离散动作 “a”,然后进一步选择一个低级连续动作 “xk”。
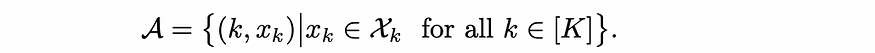
等式 1
六、参数化深度 Q 网络学习 (P-DQN)
所以现在当务之急是我们需要一个DRL算法,它直接在离散-连续混合动作空间上工作,没有近似或松弛。P-DQN可以看作是著名的DQN算法对混合动作空间的扩展。虽然它的名字只是在DQN之后,但这个算法采用了DQN和DDPG的优点。DDPG 算法是一种非常著名的算法,可以处理连续动作空间。
DQN 中心概念中的 Q(s ,a) 值,它基本上说明了给定状态“s”中动作“a”的好坏。我们需要为混合动作空间 A 定义一个类似的 Q 值,如 Eq-1 中定义的那样。类似于 Q(s ,a);让我们定义 Q(s, k, xk) 让 k 是时间 t 选择的离散动作,让 xk 是关联的连续动作。与深度 Q 网络类似,我们使用深度神经网络 Q(s, k, xk ;ω) 近似 Q(s, k, xk),其中 ω 表示网络权重。
现在一切看起来都很好,但是当我们在贝尔曼更新中直接使用 Q(s, k, xk ; ω) 时,问题就出现了。
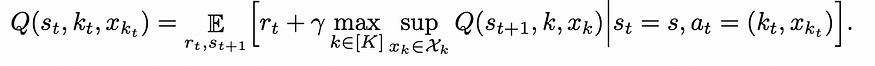
贝尔曼更新方程
如果你仔细观察贝尔曼更新中方程的右侧,就会发现离散动作“k”和连续动作xk上有一个最大步长。由于在有限的离散动作 [k] 上采用最大值,因此在计算上没有挑战性。但是在连续空间xk上取最大值在计算上是棘手的,因为网络需要迭代连续空间中的所有可能值以找出最大Q(s,k,xk)。
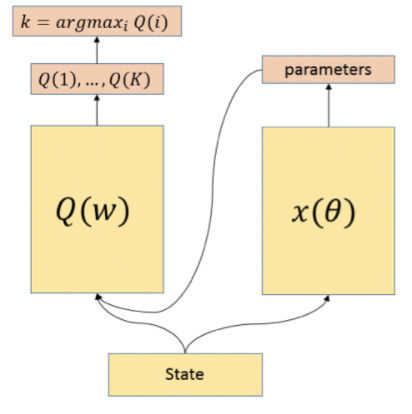
这就是我们从深度确定性策略梯度(DDPG)算法中获得一些灵感的地方。我们用确定性策略网络xk(S; θ)近似xk,其中θ表示策略网络的网络权重。
所以当 ω 固定时,我们希望找到 θ 使得:
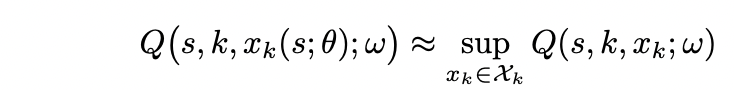
七、算法:
就像在DDPG算法中一样,我们也可以将噪声添加到动作xk(S; θ)的连续部分以进行探索。就像在DQN中一样,它使用经验回放来减少样本之间的依赖性,以及类似的贪婪ε探索技术。权重 ω 和 θ 分别以不同的学习率更新,并使用随机梯度方法更新权重。

八、结论
在此博客中,我们定义了离散-连续混合操作空间。我们提出了参数化的深度Q网络(P-DQN),它扩展了经典的DQN,为动作的连续部分提供了确定性策略。
参考资料:
1 论文:https://arxiv.org/pdf/1810.06394.pdf
Kowshik chilamkurthy