目录
一、顺序搜索
二、分析顺序搜索算法
三、二分搜索
四、分析二分搜索算法
五、散列
5.1 散列函数
5.2 处理冲突
5.3 实现映射抽象数据类型
搜索是指从元素集合中找到某个特定元素的算法过程。搜索过程通常返回True或False,分别表示元素是否存在。有时,可以修改搜索过程,使其返回目标元素的位置。
Python提供了运算符in,通过它可以方便地检查元素是否在列表中。
>>> 15 in [3,5,2,4,1]
False
>>> 3 in [3,5,2,4,1]
True一、顺序搜索
存储在列表等集合中的数据项彼此存在线性或顺序关系,每个数据项的位置与其他数据项相关。在Python列表中,数据项的位置就是它的下标。因为下标是有序的,所以能够顺序访问,由此可以进行顺序搜索。
顺序搜索的原理:从列表中的第一个元素开始,沿着默认的顺序逐个查看,直到找到目标元素或者查完列表。如果查完列表后仍没有找到目标元素,则说明目标元素不在列表中。
无序列表的顺序搜索:
def sequentialSearch(alist,item):
pos=0
found=False
while pos<len(alist) and not found:
if alist[pos]==item:
found=True
else:
pos=pos+1
return found二、分析顺序搜索算法
| 最好情况 | 最坏情况 | 普通情况 | |
|---|---|---|---|
| 存在目标元素 | 1 | n | n/2 |
| 不存在目标元素 | n | n | n |
有序列表的顺序搜索:
def orderedSequentialSearch(alist,item):
pos=0
found=False
stop=False
while pos<len(alist) and not found and not stop:
if alist[pos]==item:
found=True
else:
if alist[pos]>item:
stop=True
else:
pos=pos+1
return found只有当列表不存在目标元素时,有序排列元素才会提高顺序搜索的效率。
| 最好情况 | 最坏情况 | 普通情况 | |
|---|---|---|---|
| 存在目标元素 | 1 | n | n/2 |
| 不存在目标元素 | 1 | n | n/2 |
三、二分搜索
在顺序搜索时,如果第一个元素不是目标元素,最多还要比较n-1次。但二分搜索不是从第一个元素开始搜索,而是从中间的元素着手。如果这个元素是目标元素,那就立即停止搜索;如果不是,则可以利用列表有序的特性,排除一半的元素。如果目标元素比中间的元素大,就可以直接排除列表左半部分和中间的元素。这是因为,如果列表包含目标元素,它必定位于右半部分。
有序列表的二分搜索:
def binarySearch(alist,item):
first=0
last=len(alist)-1
found=False
while first<=last and not found:
midpoint=(first+last)//2
if alist[midpoint]==item:
found=True
else:
if item<alist[midpoint]:
last=midpoint-1
else:
first=midpoint+1
return found这个算法是分治策略的好例子。分治是指将问题分解成小问题,以某种方式解决小问题,然后整合结果,以解决最初的问题。对列表进行二分搜索时,先查看中间的元素。如果目标元素小于中间的元素,就只需要对列表的左半部分进行二分搜索。同理,如果目标元素更大,则只需对右半部分进行二分搜索。两种情况下,都是针对一个更小的列表递归调用二分搜索函数。
二分搜索的递归版本:
def binarySearch(alist,item):
if len(alist)==0:
return False
else:
midpoint=len(alist)//2
if alist[midpoint]==item:
return True
else:
if item<alist[midpoint]:
return binarySearch(alist[:midpoint],item)
else:
return binarySearch(alist[midpoint+1:],item)四、分析二分搜索算法
二分搜索算法的时间复杂度是O(logn)。
尽管二分搜索通常优于顺序搜索,但当n较小时,排序引起的额外开销可能并不划算。实际上应该始终考虑,为了提高搜索效率,额外排序是否值得。如果排序一次后能够搜索多次,那么排序的开销不值一提。然而,对于大型列表而言,只排序一次也会有昂贵的计算成本,因此从头进行顺序排序可能是更好的选择。
五、散列
通过散列可以构建一个时间复杂度为O(1)的数据结构。
散列表是元素集合,其中的元素以一种便于查找的方式存储。散列表中的每个位置通常被称为槽,其中可以存储一个元素。槽用一个从0开始的整数标记,例如0号槽、1号槽、2号槽,等等。初始情形下,散列表中没有元素,每个槽都是空的。可以用列表来实现散列表,并将每个元素初始化为Python中的特殊值None。
散列函数将散列表中的元素与其所属位置对应起来。对散列表中的任一元素,散列函数返回一个介于0和m-1之间的整数。首先来看第一个散列函数,它有时被称作“取余函数”,即用一个元素除以表的大小,并将得到的余数作为散列值。取余函数是一个很常见的散列函数,这是因为结果必须在槽编号范围内。
计算出散列值后,就可以将每个元素插入到相应的位置。在11个槽中,有六个被占用。占用率被称为载荷因子,记作,定义如下:
=元素个数/散列表大小。
搜索目标元素时,仅需使用散列函数计算出该元素的槽编号,并查看对应的槽中是否有值。因为计算散列值并找到相应位置所需的时间是固定的,所以搜索操作的时间复杂是O(1)。
如果两个元素的散列值相同,散列函数会将两个元素都放入同一个槽,这种情况叫作冲突,也叫做“碰撞”。显然,冲突给散列函数带来了问题。
5.1 散列函数
给定一个元素集合,能将每个怨怒是映射到不同的槽,这种散列函数称作完美散列函数。
我们的目标是创建这样一个散列函数:冲突数最少,计算方便,元素均匀分布于散列表中。有多种常见的方法来扩展取余函数,下面介绍其中的几种。
折叠法先将元素切成等长的部分(最后一部分的长度可能不同),然后将这些部分相加,得到散列值。假设元素是电话号码436-555-4601,以2位为一组进行切分,得到43、65、55、46和01,将这些数字相加后,得到210.假设散列表有11个槽,接着需要用210除以1,并保留余数1,所以,电话号码436-555-4601被映射到散列表的1号槽。有些折叠法更进一步,在加总前每隔一个数反转一次。就本例而言,反转后的结果是:43+56+55+64+01=219,219%11=10。
另一个构建散列函数的数学技巧是平方取中法:先将元素取平方,然后提取中间几位数。如果元素是44,先计算44*44=1936,然后提取中间两位93,继续进行取余的步骤,得到5(93%11)。
我们也可以为基于字符的元素(比如字符串)创建散列函数。可以将单词"cat"看作序数值序列,如下所示:
>>> ord('c')
99
>>> ord('a')
97
>>> ord('t')
116因此,可以将这些序数值相加,并采用取余法得到散列值。
def hash(astring,tablesize):
sum=0
for pos in range(len(astring)):
sum=sum+ord(astring[pos])
return sum%tablesize有趣的是,针对异序词,这个散列函数总是得到相同的散列值。要弥补这一点,可以同字符位置作为权重因子。
def hash(astring,tablesize):
sum=0
for pos in range(len(astring)):
sum=sum+ord(astring[pos])*(pos+1)
return sum%tablesize5.2 处理冲突
当两个元素被分到同一个槽中时,必须通过一种系统化方法在散列表中安置第二个元素。这个过程被称为处理冲突。
一种方法是在散列表中找到另一个空槽,用于放置引起冲突的元素。简单的做法是从起初的散列值开始,顺序遍历散列表,知道找到一个空槽。注意,为了遍历散列表,可能需要往回检查第一个槽。这个过程被称为开放定址法,它尝试在散列表中寻找下一个空槽或地址。由于是逐个访问槽,因此这个做法被称作线性探测。
线性探测有个缺点,那就是会使散列表中的元素出现聚集现象。也就是说,如果一个槽发生太多冲突,线性探测会填满附近的槽,而这会影响后续插的元素。要避免元素聚集,一种方法是扩展线性探测,不再依次顺序查找空槽,而是跳过一些槽,这样做能使引起冲突的元素分布得更均匀。采用“加3”探测策略处理冲突后的元素是指发生冲突时,为了找到空槽,该策略每次跳两个槽。
再散列泛指在发生冲突后寻找另一个槽的过程。采用线性探测时,再散列函数是newhashvalue=rehash(oldhanshvalue),并且rehash(pos)=(pos+1)%sizeoftable。“加3”探测策略的再散列函数可以定义为rehash(pos)=(pos+3)%sizeoftable。也就是说,可以将再散列函数定义为rehash(pos)=(pos+skip)%sizeoftable。注意,“跨步(skip)的大小要能够保证表中所有的槽最终都被访问到,否则就会浪费槽资源。要保证这一点,常常建议散列表的大小为素数。
平方探测是线性探测的一个变体,它不采用固定的跨步,而是通过再散列函数递增散列值。如果第一个散列值是h,后续的散列值就是h+1、h+4、h+9、h+16,等等。换句话说,平方探测的跨步是一系列完全平方数。
另一种处理冲突的方法就是让每个槽有一个指向元素集合(或链表)的引用。链接法允许散列表中的同一个位置上存在多个元素。发生冲突时,元素仍然被插入其散列值对应的槽中。不过,随着同一个位置上的元素越来越多,搜索变得越来越困难。
5.3 实现映射抽象数据类型
字典是最有用的Python集合之一。字典是存储键-值对的数据类型。键用来查找关联的值,这个概念常常被称作映射。
映射抽象数据类型定义如下。它是将键和值关联起来的无序集合,其中的键是不重复的,键和值之间是一一对应的关系。映射支持以下操作。
- Map()创建一个空的映射,它返回一个空的映射集合。
- put(key,val)往映射中加入一个新的键值对。如果键已经存在,就用新值替换旧值。
- get(key)返回key对应的值。如果key不存在,则返回None。
- del通过del map[key]这样的语句从映射中删除键-值对。
- len()返回映射中存储的键-值对的数目。
- in通过key in map这样的语句,在键存在时返回True,否则返回False。
class HashTable:
def __init__(self):
self.size=11
self.slots=[None]*self.size
self.data=[None]*self.size
def put(self,key,data):
hashvalue=self.hashfunction(key,len(self.slots))
if self.slots[hashvalue]==None:
self.slots[hashvalue]=key
self.data[hashvalue]=data
else:
if self.slots[hashvalue]==key:
self.data[hashvalue]=data #替换
else:
nextslot=self.rehash(hashvalue,len(self.slots))
while self.slots[nextslot]!=None and self.slots[nextslot]!=key:
nextslot=self.rehash(nextslot,len(self.slots))
if self.slots[nextslot]==None:
self.slots[nextslot]=key
self.data[nextslot]=data
else:
self.data[nextslot]=data #替换
def hashfunction(self,key,size):
return key%size
def rehash(self,oldhash,size):
return (oldhash+1)%size
def get(self,key):
startslot=self.hashfunction(key,len(self.slots))
data=None
stop=False
found=False
position=startslot
while self.slots[position]!=None and not found and not stop:
if self.slots[position]==key:
found=True
data=self.data[position]
else:
position=self.rehash(position,len(self.slots))
if position==startslot:
stop=True
return data
def __getitem__(self, key):
return self.get(key)
def __setitem__(self, key, data):
self.put(key,data)
if __name__=="__main__":
H=HashTable()
H[54]="cat"
H[26]="dog"
H[93]="lion"
H[17]="tiger"
H[77]="bird"
H[31]="cow"
H[44]="goat"
H[55]="pig"
H[20]="chicken"
print(H.slots)
print(H.data)
print(H[20])
print(H[17])
H[20]="duck"
print(H[20])
print(H.data)
print(H[99])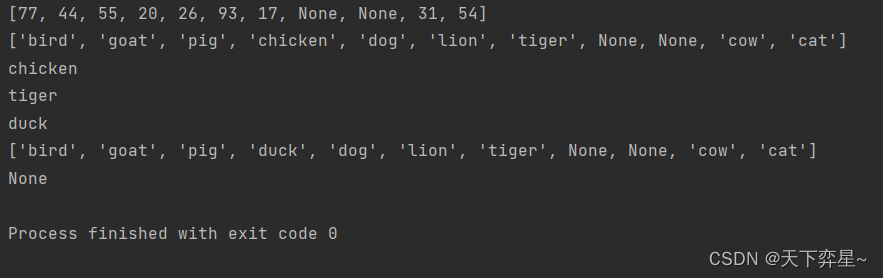
HashTable类的最后两个方法提供了额外的字典功能。我们重载__getitem__和__settiem__ ,以通过[ ]进行访问。这意味着创建HashTable类之后,就可以使用熟悉的索引运算符了。



![[回馈]ASP.NET Core MVC开发实战之商城系统(五)](https://img-blog.csdnimg.cn/img_convert/d851b996d65c529cd26a2e7695628207.png)




![[openCV]基于拟合中线的智能车巡线方案V3](https://img-blog.csdnimg.cn/6d6e0e96c2dc49d2b5af82306de736db.png)