文章目录
- 1. JZ4 二维数组中的查找
- 暴力法
- 右上角往左下角逼近
- 二分查找-左闭右开区间
- 2. 替换空格
- 3. JZ6 从尾到头打印链表
- 4. JZ7 重建二叉树
- 思路1
- 哈希加速
- 5. JZ9 用两个栈实现队列
- 6. JZ11 旋转数组的最小数字
- 常规遍历
- 二分法
- 7. 斐波那契数列
- 动态规划
- 递归
- 8. JZ69 跳台阶
- 动态规划
- 递归
- 9. JZ71 跳台阶扩展问题
- 动态规划-看题解
- 动态规划-优化空间
- 数学规律-优化时间空间-左移运算
- 10. JZ70 矩形覆盖
- 动态规划 数组写法
- 动态规划 三个变量
- 补充内容:左移运算符与右移运算符
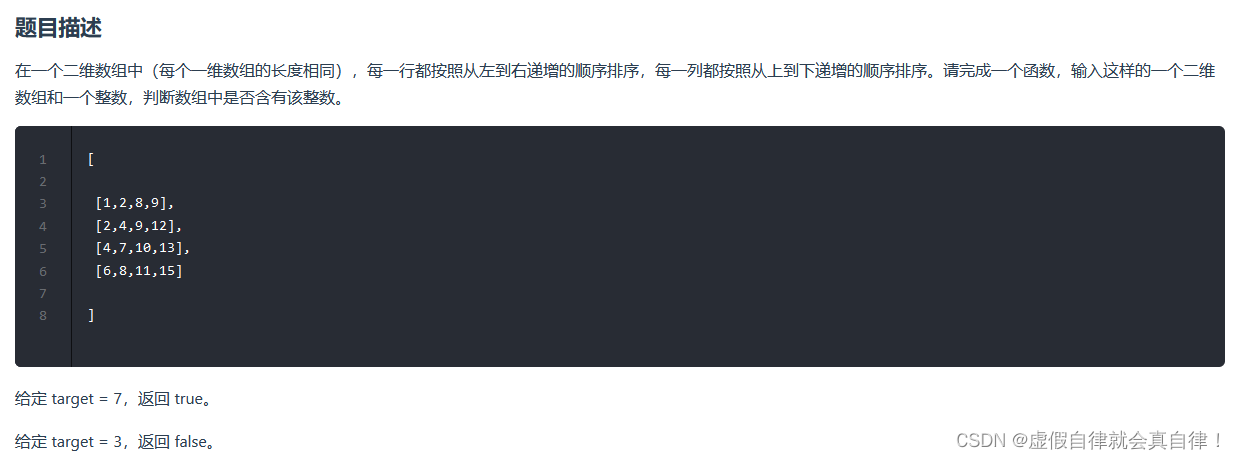
1. JZ4 二维数组中的查找
暴力法
两层for循环,自测可通过,超时,时间复杂度m*n
右上角往左下角逼近
利用递增,右上角为分割点
bool Find(int target, vector<vector<int> >& array) {
//右上角逐渐逼近左下角 递增
if(array.empty() || array[0].empty()) return false;
int row = array[0].size();
int col = array.size();
int w = row - 1, h = 0;
while(w >= 0 && h < col)
{
if(array[h][w] > target) w--;//array[h][w]表示右上角 target在左边 往左走
else if(array[h][w] < target) h++;//target在下面 往下走
else return true;
}
return false;
}
二分查找-左闭右开区间
也可以是左闭右闭区间实现
bool Find(int target, vector<vector<int> >& array) {
//二分查找
if(array.empty() || array[0].empty()) return false;
//遍历每一行 二分
for(int i=0; i<array.size(); i++)
{
if(binaryfind(array[i], target)) return true;
}
return false;
}
bool binaryfind(vector<int>nums, int target)
{
//左闭右开区间
int start = 0, end = nums.size();
int mid = 0;
for(int i=0; i<nums.size(); i++)
{
mid = start + (end - start) / 2;
if(target < nums[i]) end = mid;
else if(target > nums[i]) start = mid + 1;
else return true;
}
return false;
}
2. 替换空格
题目:请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy
统计空格长度,倒序遍历替换
第一次写的时候用的是for(int i=length; i>=0 && i<newlen; i--)条件
这次写的时候用的是for(int i=length; i>=0 && newlen!=i; i--)条件
class Solution {
public:
void replaceSpace(char *str,int length) {
int spacelen = 0;
for(int i=0; i<length; i++)
{
if(str[i] == ' ') spacelen++;
}
int newlen = length + 2*spacelen;
//替换 如果newlen=i 说明此时前面已经都没有空格了,可以节约一部分时间,而不是一直赋值下去
for(int i=length; i>=0 && newlen!=i; i--)
//for(int i=length; i>=0 && i<newlen; i--)
{
if(str[i] == ' ')
{
str[newlen--] = '0';
str[newlen--] = '2';
str[newlen--] = '%';
}
else str[newlen--] = str[i];
}
int spaceCount = 0;
}
};
3. JZ6 从尾到头打印链表
题目:输入一个链表,按链表从尾到头的顺序返回一个ArrayList
正序保存,然后reverse返回。或者返回逆序
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) :
* val(x), next(NULL) {
* }
* };
*/
#include <algorithm>
class Solution {
public:
vector<int> printListFromTailToHead(ListNode* head) {
if(head == NULL) return vector<int>();
//正序保存+reverse
vector<int> result;
ListNode* cur = head;
while(cur)
{
result.push_back(cur->val);
cur = cur->next;
}
/*
reverse(result.begin(), result.end());
return result;
*/
return vector<int>(result.rbegin(),result.rend());
}
};
4. JZ7 重建二叉树
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
力扣上有一道题是根据中序和后序遍历结果重建树,106. 从中序与后序遍历序列构造二叉树,这道题是根据中序和前序遍历结果重建树。
思路1
根节点分割中序遍历结果,左子树节点数分割前序遍历结果
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
#include <iterator>
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param preOrder int整型vector
* @param vinOrder int整型vector
* @return TreeNode类
*/
TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {
if (preOrder.size() == 0 || vinOrder.size() == 0) {
return NULL;
}
//distance两个迭代器之间元素个数 find查找两个迭代器之间是否有元素preOrder[0]
int rootindex = distance(vinOrder.begin(), find(vinOrder.begin(), vinOrder.end(), preOrder[0]));
//前序遍历 左闭右开区间 左子树 右子树分割 利用节点个数 注意去掉根节点
vector<int> left_pre(preOrder.begin() + 1, preOrder.begin() + 1 + rootindex);
vector<int> right_pre(preOrder.begin() + 1 + rootindex, preOrder.end());
//中序遍历 左闭右开区间 左子树 右子树分割 利用根节点
vector<int> left_vin(vinOrder.begin(), vinOrder.begin() + rootindex);
vector<int> right_vin(vinOrder.begin() + rootindex + 1, vinOrder.end());
//递归构造
TreeNode* head = new TreeNode(preOrder[0]);
head->left = reConstructBinaryTree(left_pre, left_vin);
head->right = reConstructBinaryTree(right_pre, right_vin);
return head;
}
};
哈希加速
/**
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param preOrder int整型vector
* @param vinOrder int整型vector
* @return TreeNode类
*/
TreeNode* reConstructBinaryTree(vector<int>& preOrder, vector<int>& vinOrder) {
//哈希加速
unordered_map<int, int> hashmap;
for(int i=0; i<vinOrder.size(); i++)
{
hashmap.insert(make_pair(vinOrder[i], i));
}
//递归
return tralversal(hashmap, preOrder, 0, vinOrder, 0, vinOrder.size()-1);
}
TreeNode* tralversal(unordered_map<int, int>& hashmap, vector<int>& pre, int start_pre, vector<int>& vin, int start_vin, int end_vin)
{
//可以取等号
if(start_pre > pre.size() || start_vin > end_vin) return nullptr;
TreeNode* root = new TreeNode(pre[start_pre]);
int rootindex = hashmap[pre[start_pre]];
//第三个参数是 前序遍历中左子树的 头结点 索引位置
//第五、六参数是索引范围是中序遍历的左子树区间 start_vin~rootindex - 1 左闭右闭
root->left = tralversal(hashmap, pre, start_pre+1, vin, start_vin, rootindex - 1);
//第三个参数是 前序遍历中右子树的 头结点 索引位置 在前序遍历中是start_pre+1+左子树节点数
//第五、六参数是索引范围是中序遍历的右子树区间 rootindex+1~end_vin 左闭右闭
root->right = tralversal(hashmap, pre, start_pre+1+rootindex-start_vin, vin, rootindex+1, end_vin);
return root;
}
};
5. JZ9 用两个栈实现队列
题目描述:完成队列的Push和Pop操作。 队列中的元素为int类型
两个栈实现,一个保存元素,一个辅助
class Solution
{
public:
void push(int node) {
stack1.push(node);
}
int pop() {
//队列是双头 先入先出;栈是单头 先进后出 所以要倒序一下
while(stack1.size() != 1)//保留栈底元素
{
stack2.push(stack1.top());
stack1.pop();
}
int target = stack1.top();
stack1.pop();
//剩下的元素再放回去stack1中
while (!stack2.empty()) {
stack1.push(stack2.top());
stack2.pop();
}
return target;
}
private:
stack<int> stack1;//保存元素
stack<int> stack2;//辅助栈
};
6. JZ11 旋转数组的最小数字
题目描述:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
常规遍历
class Solution {
public:
int minNumberInRotateArray(vector<int>& nums) {
if(nums.size() == 0) return 0;
//遍历整个数组
for(int i=0; i<nums.size(); i++)
{
if(nums[i] > nums[i+1]) return nums[i+1];
}
return nums[0];
}
};
二分法
class Solution {
public:
int minNumberInRotateArray(vector<int>& nums) {
if(nums.size() == 0) return 0;
//二分法 左闭右开 最值在两头
int left = 0, right = nums.size()-1;
while(left+1 < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < nums[right]) right = mid;//说明右边有序,那就向左边走
else if(nums[mid] == nums[right]) right = right-1;
else left = mid;
}
return min(nums[left], nums[right]);
}
};
7. 斐波那契数列
题目描述:大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0,第1项是1)。n≤39
动态规划
三个数值保存在一个数组,注意最后返回值是n-1对3取余数
class Solution {
public:
int Fibonacci(int n) {
if(n == 1 || n == 2) return 1;
if(n == 3) return 2;
vector<int> F(3);
F[0] = 1;
F[1] = 1;
F[2] = 2;
for(int i=3; i<n; i++)
{
F[i % 3] = F[(i-1) % 3] + F[(i-2) % 3];
}
return F[(n-1) % 3];
}
};
递归
class Solution {
public:
int Fibonacci(int n) {
//递归
if(n == 0) return 0;
if(n == 1 || n == 2) return 1;
return Fibonacci(n-1) + Fibonacci(n-2);
}
};
8. JZ69 跳台阶
题目描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
相当于斐波那契数列
动态规划
动态规划的定义是跳n级台阶有多少种跳法
class Solution {
public:
int jumpFloor(int number) {
//动态规划
if(number == 1) return 1;
if(number == 2) return 2;
vector<int> dp(3);
dp[0] = 1;
dp[1] = 2;
for(int i=2; i<number; i++)
{
dp[i % 2] = dp[(i-1) % 2] + dp[(i-2) % 2];
}
return dp[(number-1) % 2];
}
};
递归
class Solution {
public:
int jumpFloor(int number) {
//递归
if(number == 1) return 1;
if(number == 2) return 2;
return jumpFloor(number-1) + jumpFloor(number-2);
}
};
9. JZ71 跳台阶扩展问题
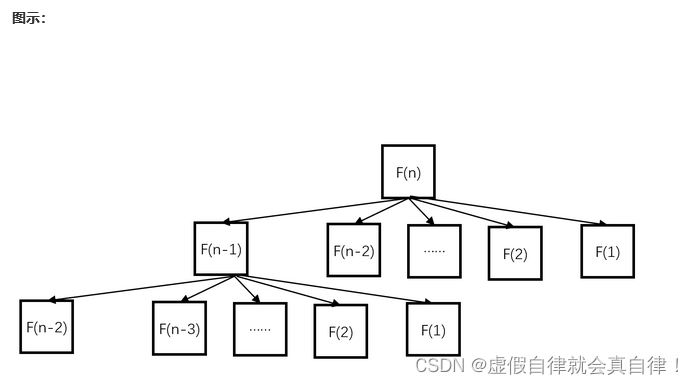
题目描述:一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
动态规划-看题解
时间复杂度: O ( n ) O(n) O(n),其中n为台阶数,一次遍历;空间复杂度: O ( n ) O(n) O(n),辅助数组dp的长度为n

class Solution {
public:
int jumpFloorII(int number) {
//动态规划-题解
vector<int> dp(number+1);
dp[0] = 1;
dp[1] = 1;
for(int i=2; i<=number; i++) dp[i] = 2 * dp[i-1];
return dp[number];
}
};
动态规划-优化空间
在上面看了题解写之后,优化了空间,时间复杂度: O ( n ) O(n) O(n);空间复杂度: O ( 1 ) O(1) O(1)
class Solution {
public:
int jumpFloorII(int number) {
//动态规划-空间优化
vector<int> dp(3);
dp[0] = 1;
dp[1] = 1;
for(int i=2; i<=number; i++)
{
dp[i % 2] = 2 * dp[(i-1) % 2];
}
return dp[number % 2];
}
};
数学规律-优化时间空间-左移运算


时间复杂度:
O
(
1
)
O(1)
O(1),一次位运算;空间复杂度:
O
(
1
)
O(1)
O(1)。
通过左移运算求幂次方来优化时间复杂度,也就是说pow(2, number - 1) 等价于 1<<number-1, 1<<number-1就是将1左移number-1位
class Solution {
public:
int jumpFloorII(int number) {
//数学规律-时间优化
if(number <= 1) return 1;
//return pow(2, number - 1);//计算2的number-1次方 时间复杂度是n 空间是1
return 1<<number-1;//将1左移number-1位 通过左移运算求幂次方 时间/空间复杂度是1
}
};
10. JZ70 矩形覆盖
题目描述:我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2n的大矩形,总共有多少种方法?注意:约定 n == 0 时,输出 0
比如n=3时,23的矩形块有3种覆盖方法,如下

宽度永远是2,那么题目换个说法就是,用n个边长为1的短线可以变成边长为n的长线,总共有多少种方法?也就是n个1变成n,一共有多少种办法?其实就是斐波那契额数列。
动态规划 数组写法
class Solution {
public:
int rectCover(int number) {
if(number <= 2) return number;
vector<int> dp(3);
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
for(int i=3; i<=number; i++)
{
dp[i % 3] = dp[(i-1) % 3] + dp[(i-2) % 3];
}
return dp[number % 3];
}
};
动态规划 三个变量
class Solution {
public:
int rectCover(int number) {
if(number <= 2) return number;
//动态规划 三个变量
int first = 1, second = 2, third = 0;
for(int i=3; i<=number; i++)
{
third = first + second;
//下一轮计算前要更新
first = second;
second = third;
}
return third;
}
};
补充内容:左移运算符与右移运算符
<<左移运算符,逻辑移位:expr1 << expr2,表示 expr1 左移 expr2 位,数值上表示 expr1 扩大了 2^expr2 倍;>>右移运算符,算术移位:expr1>>expr2,表示 expr2 右移 expr2 位,数值上表示 expr1 缩小了 2^expr2 倍;- 左边的数表示被移位的数字,1<<n = 2^n,n<<1 = 2*n。左移就是扩大2的移位数次方,右移就是缩小2的移位数次方