1.插入排序

1.1代码

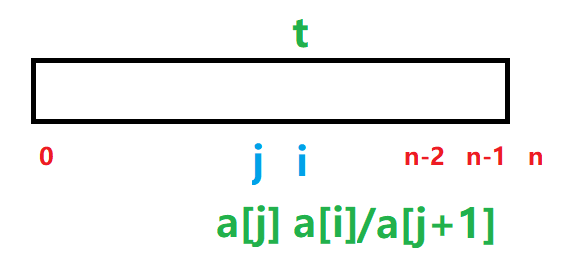
在这里插入图片描述

//插入排序1.0
/*
void InsertSort(int* a, int n)
{
	//i： 0 -- 倒数第2个元素
	for (int i = 0; i < n - 1; ++i)
	{
		//end记录i
		int end = i;
		//tmp记录end后一个值
		int tmp = a[end + 1];
		//把tmp与tmp前的每一个数比较 若小于则前面数据后移
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				--end;
			}
			else
			{
				break;
			}
		}
		//遇到<=tmp的数 或 tmp前数据遍历完毕 循环终止 把tmp放到目的地
		a[end + 1] = tmp;
	}
}
*/

//插入排序2.0--在这个版本中默认第一个已排好序 在内层for中会与i前的比较 
//直接插入排序没什么问题 但是在下面的希尔排序 第一个元素不能被默认为已经有序
//所以插入排序3.0更好一些 对下面的代码复用起到很好的作用
/*
void InsertSort(int* a, int n)
{
	int i, j, t;
	for (i = 1; i < n; i++)  //i：1 ~ n-1 a[0]默认已排好序
	{
		//临时变量t记录a[i]的值  下面程序a[i]会被修改
		t = a[i];
		//遍历i前所有数据 把比a[i]大的都向后移
		for (j = i - 1; j >= 0 && t < a[j]; j--)
			a[j + 1] = a[j];
		//j的初值为i-1  j!=i-1：i前有比a[i]大的 a[j]移到a[j+1]
		//此时内层for循环已终止 表明i前数据已有序 需要把原a[i]插到合适位置
		if (j != i - 1)
			a[j + 1] = t;
	}
}
*/

//插入排序3.0
void InsertSort(int* a, int n)
{
	int i, j, t;
	for (i = 0; i < n - 1; i++)
	{
		t = a[i + 1];
		for (j = i; j >= 0 && t < a[j]; j--)
			a[j + 1] = a[j];
		if (j != i)
			a[j + 1] = t;
	}
}

1.2复杂度

适用：数据越接近有序，插入排序效率越高
最坏（逆序）：O(N^2)
最优（顺序/接近顺序）：O(N)

2.希尔排序

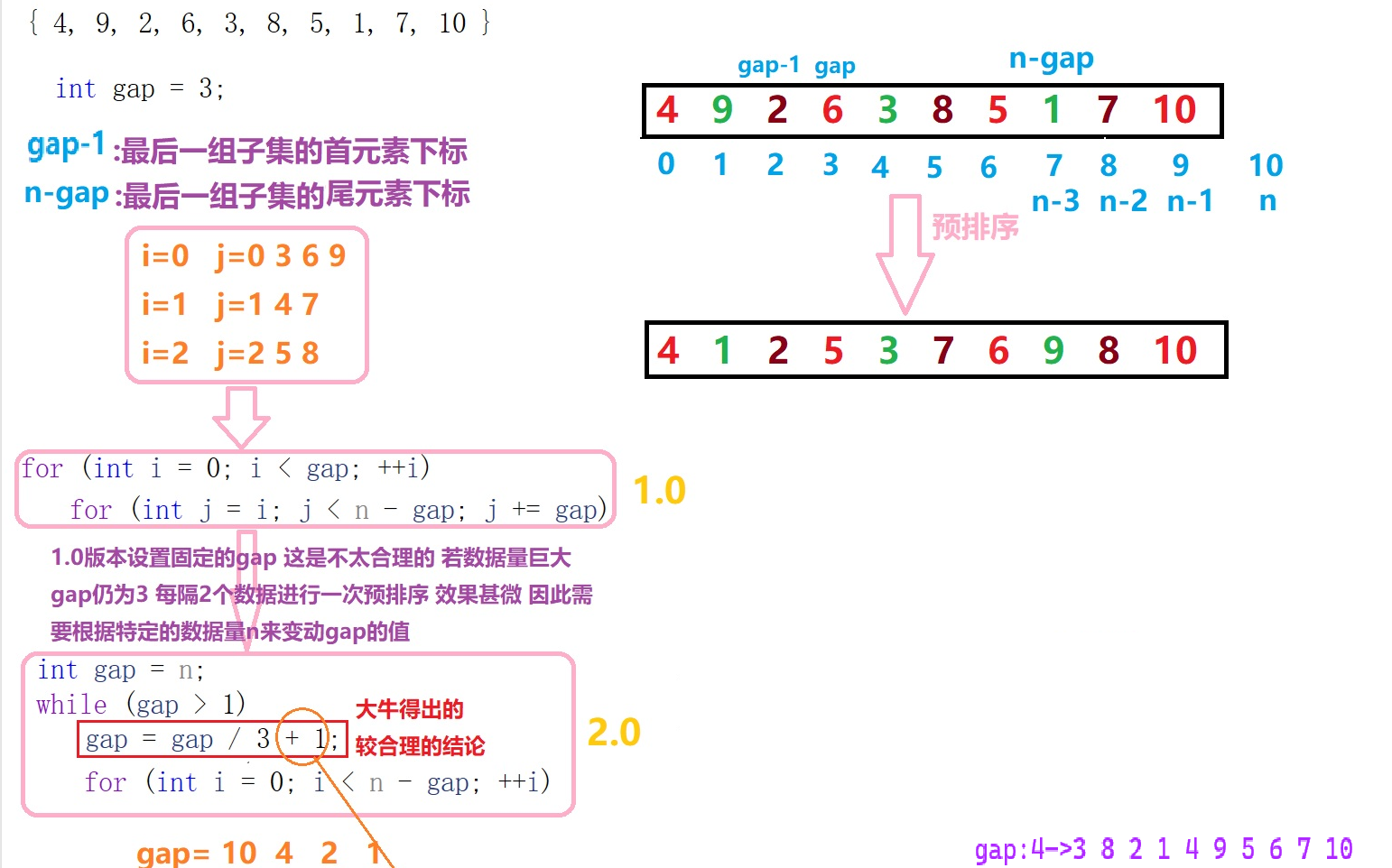
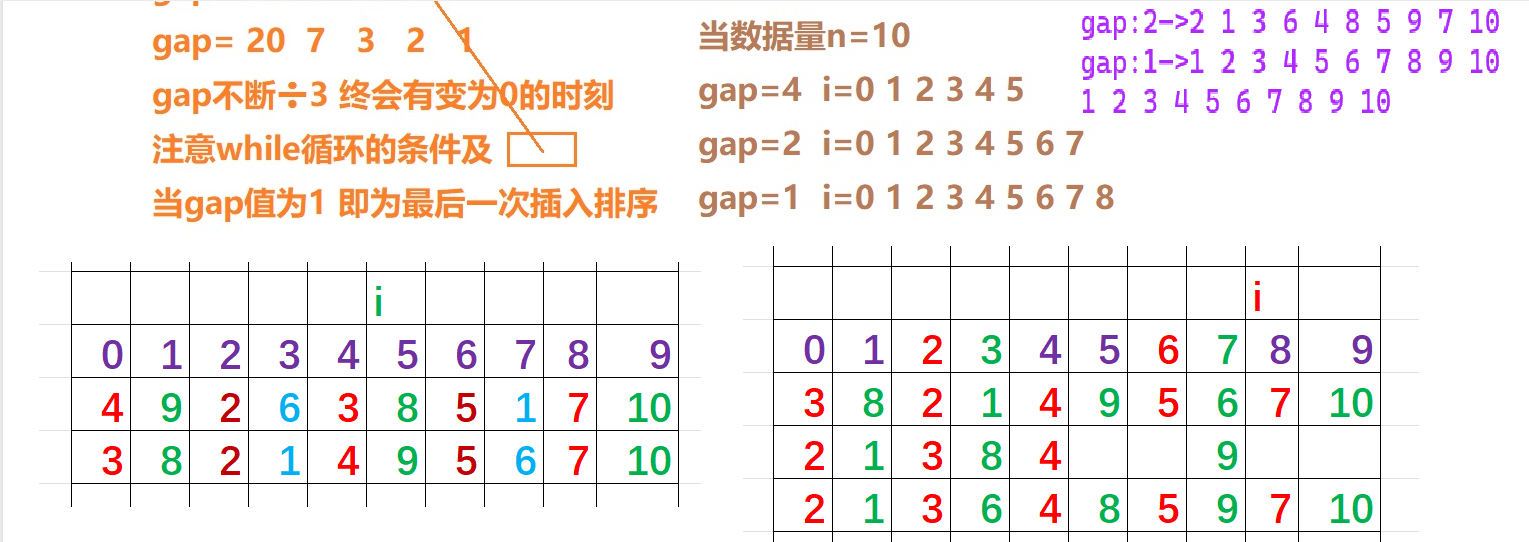
在这里插入图片描述

2.1代码

//希尔排序1.0--平均：O(N^1.3）
/*
void ShellSort(int* a, int n)
{
	int gap = 3;

	for (int i = 0; i < gap; ++i)
	{
		for (int j = i; j < n - gap; j += gap)
		{
			int end = j;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}
	}
    PrintArray(a, n);
}
*/
//希尔排序2.0
/*
void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;

		for (int i = 0; i < n - gap; ++i)
		{
			int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (tmp < a[end])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}

		printf("gap:%d->", gap);
		PrintArray(a, n);
	}
}
*/

//希尔排序3.0
void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		int i, j, t;
		for (i = 0; i < n - gap ; ++i)
		{
			t = a[i + gap];
			for (j = i ; j >= 0 && t < a[j]; j-=gap)
			{
				a[j + gap] = a[j];
			}
			if (j != i)
				a[j + gap] = t;
		}
		printf("gap:%d->", gap);
		PrintArray(a, n);
	}
}