一、思路
递归
二、解题方法
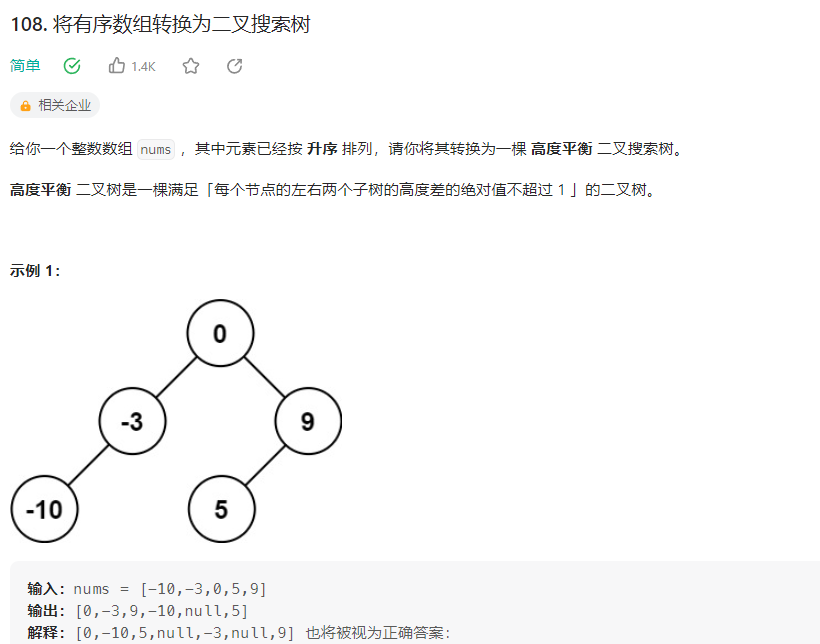
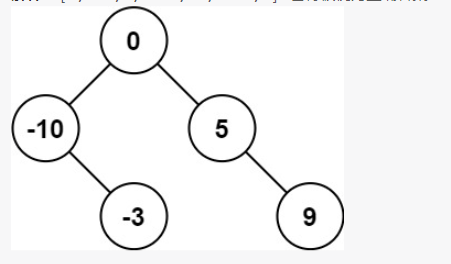
在给定中序遍历序列数组的情况下,每一个子树中的数字在数组中一定是连续的,因此可以通过数组下标范围确定子树包含的数字,下标范围记为 [left,right]。对于整个中序遍历序列,下标范围从 left=0到 right=nums.size()−1。当 left>right 时,平衡二叉搜索树为空。
选择中间位置左边的数字作为根节点
三、code
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return helper(nums,0,nums.size()-1);
}
TreeNode* helper(vector<int>& nums,int left,int right)
{
if(left>right)//当左边界 left 大于右边界 right 时,意味着当前处理的区间为空,即没有元素可以用来构建子树了。这种情况下,我们返回 nullptr,表示当前子树为空树。
{
return nullptr;
}
int mid=(left+right+1)/2;//计算当前处理区间的中间位置,总是选择中间位置左边的数字作为根节点。这样可以保证构建的二叉搜索树是高度平衡的。
TreeNode* root=new TreeNode(nums[mid]);//创建当前区间中间位置的元素值为根节点的二叉树节点。
root->left=helper(nums,left,mid-1);//递归构建当前根节点的左子树,将左边界设为 left,右边界设为中间位置的前一个位置 mid - 1。
root->right=helper(nums,mid+1,right);//递归构建当前根节点的右子树,将左边界设为中间位置的后一个位置 mid + 1,右边界设为 right。
return root;
}
};=========================================================================学到的知识:
①
前序遍历(Preorder Traversal):在二叉树中,先访问根节点,然后按照左子树、右子树的顺序递归遍历子树。在前序遍历中,根节点的访问顺序是最先的。
中序遍历(Inorder Traversal):在二叉树中,先按照左子树、根节点、右子树的顺序递归遍历子树。在中序遍历中,根节点的访问顺序位于左右子树之间。
后序遍历(Postorder Traversal):在二叉树中,先按照左子树、右子树、根节点的顺序递归遍历子树。在后序遍历中,根节点的访问顺序是最后的。
这三种遍历方式是深度优先搜索(DFS)的三种不同变种。它们分别有不同的应用场景:
- 前序遍历:适用于需要先处理根节点再处理子节点的场景,比如复制整个树的结构或序列化为字符串。
- 中序遍历:适用于二叉搜索树,可以将其按从小到大的顺序输出,比如查找树中第 k 小的元素。
- 后序遍历:适用于释放二叉树的内存,先释放子节点再释放根节点,以防止访问已经释放的内存。
②TreeNode* root = new TreeNode(nums[mid]);
这行代码用于创建一个新的二叉树节点,并将其值初始化为有序数组中间位置的元素 nums[mid]