1. 跑步运动为例，对运动进行时序分析

时序数据是指时间序列数据，是按照时间顺序排列的数据集合，每个数据点都与一个特定的时间戳相关联。在跑步活动中，我们可以将每次跑步的数据记录作为一个时序数据样本，每个样本都包含跑步时间、配速、心率、步频、距离等要素。

这些跑步数据的时序特征不仅包含了跑步活动本身的信息，还可以反映出跑者的训练水平、身体状况、体能改进等方面的变化。通过对这些时序数据进行分析，我们可以探索以下内容：

趋势分析：查看跑步时间、配速、心率、步频、距离等在时间上的变化趋势，了解训练或比赛表现的变化情况。
周期性分析：探索跑步活动在一天内、一周内、一个月内的周期性变化，发现可能的规律和趋势。
异常检测：检测跑步数据中的异常值，如异常的心率波动、超出正常范围的配速等，帮助发现潜在问题。
关联分析：分析跑步数据中各个特征之间的相关性，了解不同要素之间的影响和关联关系。
训练效果评估：通过分析跑步数据，评估训练计划的效果，调整训练策略，达到最佳训练效果。

时序数据分析对于跑步活动的训练和竞技表现具有重要的意义。通过合理的时序数据记录和分析，跑者可以更好地了解自己的训练状态，找到改进和优化的方向，不断提升自己的跑步水平。而在这个过程中，Pandas 的强大功能将为我们提供极大的帮助，让我们能够从海量的时序数据中挖掘出更深层次的洞察和价值。

2. Pandas时序数据处理和分析的特点

Pandas 是 Python 中用于数据处理和分析的强大库，在处理时序数据方面有着独特的特点和优势。下面我们来看一下 Pandas 在时序数据处理上的特点和优势：

内置的日期和时间支持： Pandas 提供了丰富的日期和时间处理功能，包括日期范围生成、日期转换、日期格式化等。它支持时间戳、日期索引和时间间隔的操作，使得处理时间序列数据更加便捷。
时间索引： Pandas 的时间序列数据通常使用时间索引，这使得数据在时间上有序排列，方便对时间序列进行切片、聚合、过滤等操作。时间索引的应用可以使得时间序列数据更易于处理和理解。
时间重采样：时间序列数据可能存在不同的采样频率，Pandas 提供了时间重采样的功能，可以将时间序列数据转换为不同的时间频率，如从分钟数据生成小时数据、从小时数据生成每天的数据等。
滚动窗口操作： Pandas 支持滚动窗口操作，可以方便地进行滑动统计、移动平均等计算。这在时序数据分析中非常常用，用于平滑数据、计算滑动窗口内的统计指标等。
时间偏移： Pandas 提供了时间偏移的功能，可以对时间序列进行移动，如前移、后移若干时间步长，这对于计算时间序列的差分和时间差等操作非常有用。
时区处理： Pandas 支持时区处理，可以在时间序列数据中指定和转换时区，方便处理不同时区的数据。
缺失值处理： Pandas 提供了灵活的缺失值处理方法，可以对时间序列数据中的缺失值进行填充或剔除，保证数据的完整性和准确性。
时间序列绘图： Pandas 结合了 Matplotlib 和 Seaborn 等绘图库，提供了简便的时间序列绘图功能，可以轻松地绘制时序数据的折线图、散点图、箱线图等。
时间序列的合并和拆分： Pandas 可以将多个时间序列数据进行合并和拆分，方便进行不同时间范围的数据组合和拆解。

总体来说，Pandas 在时序数据处理上具有非常丰富和强大的功能，它的设计和实现使得处理时间序列数据变得高效而直观。无论是数据清洗、预处理、特征工程，还是时间序列的可视化和建模，Pandas 都为数据分析师和数据科学家提供了便捷的工具，接下来，我们将以运动数据分析展开，使用上述功能进行数据分析。

3. 快速入门，建立跑步时序数据集

快速入门 Pandas 并进行跑步数据的时序分析，可以按照以下步骤进行。

3.1. 读取原始数据

我们把运动数据记录在csv格式文件中，例如文中的数据文件为”运动记录202307.csv”。

csv全称“Comma-Separated Values”，是一种逗号分隔值格式的文件，是一种用来存储数据的纯文本格式文件。CSV文件由任意数目的记录组成，记录间以某种换行符分隔；每条记录由字段组成，字段间的分隔符是其它字符或字符串。

import pandas as pd
df = pd.read_csv('运动记录202307.csv', encoding='utf_8_sig')
df

在这里插入图片描述

3.2. 建立时序数据

用于补齐时间序列

import pandas as pd

# 创建间隔30分钟的时间序列
#times = pd.date_range(start='2023-07-28 00:00:00', end='2023-07-30 23:59:59',freq='30min')  
times = pd.date_range(start='2023-05-01', end= '2023-07-30', freq='D') 
# 按天建立时间序列集
times = pd.DataFrame(times,columns=['RecordTime'])
# 前10条记录
times.head(10)

# 截取实际数据日期，按日建立时序
#df['RecordTime'] = df['时间'].dt.strftime('%Y-%m-%d')
df['RecordTime'] = df['时间'].str[0:11]
# 转换为时间类型
df['RecordTime'] = df['RecordTime'].astype('datetime64')
# 以时间序列为主，左关联数据
df = pd.merge(left=times, right=df,on='RecordTime',how='left')
# 取最后10条记录
df.tail(10)

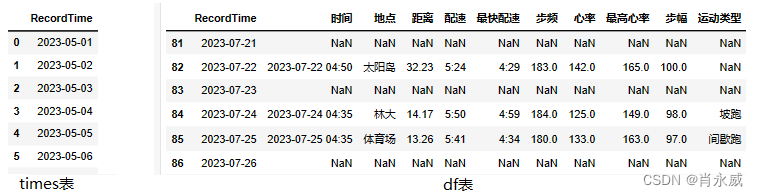
在这里插入图片描述
如图所示，右侧“df表”，出现空值（NaN）的，为时序缺失数据。

3.3. 相关性分析

大数据时代，“我们不再热衷于寻找因果关系，而应该寻找事物之间的相关关系。

“万物皆有联”，是大数据一个最重要的核心思维。

所谓联，这里指的就是事物之间的相互影响、相互制约、相互印证的关系。而事物这种相互影响、相互关联的关系，就叫做相关关系，简称相关性。

我们先以相关分析为例，研究运动数据项间得相关性，使用**Pearson相关系数 (Pearson Correlation)**算法计算。

皮尔森相关系数是一种最简单的，能帮助理解特征和响应变量之间关系的方法，该方法衡量的是变量之间的线性相关性，结果的取值区间为 $[- 1 ， 1]$ ，-1表示完全的负相关，+1表示完全的正相关，0表示没有线性相关。

$\rho_{X,Y}=\frac{cov(X,Y)}{\sigma _{X}\sigma_{Y}}$

$\rho_{X,Y}=\frac{\sum_{i=1}^{n}(X_{i}-\overline{X})(Y_{i}-\overline{Y})}{\sqrt{\sum_{i=1}^{n}(X-\overline{X})^{2}}\sqrt{\sum_{i=1}^{n}(Y-\overline{Y})^{2}}}$

在相关分析中，所讨论的变量的地位一样，分析侧重于随机变量之间的种种相关特征。例如，以 $X$ 、 $Y$ 分别记小学生的数学与语文成绩，感兴趣的是二者的关系如何，而不在于由 $X$ 去预测 $Y$ 。

而使用pandas，使这种复杂的计算变得非常简单，速度快、易于计算，经常在我们数据分析员拿到数据（经过清洗和特征提取）之后第一时间所做的分析。

# 再去掉空值
df2 = df.loc[~df['时间'].isnull()]
# 时间转化为秒
df2['配速'] = df2['配速'].str[0:1].astype(int)*60 + df2['配速'].str[2:4].astype(int)
df2['最快配速'] = df2['最快配速'].str[0:1].astype(int)*60 + df2['最快配速'].str[2:4].astype(int)
# 计算皮尔逊相关
corr = df2[['时间','地点','距离','配速','最快配速','步频','心率','最高心率','步幅']].corr(method='pearson',min_periods=1)

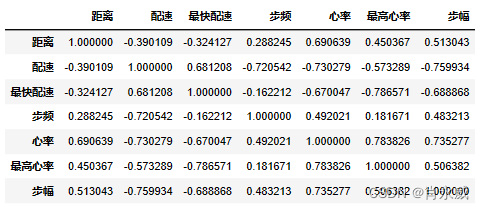
在这里插入图片描述

时间数据很特殊，我们需要转换为统一量中进行对比，这里统一转换为秒。

3.4. 可视化

3.4.1. Pandas可视化

Pandas绘图是基于Matplotlib而成的，所以既可以对Series绘图，也可以对DataFrame绘图。下面是一个简单的示例，绘制柱状图：

# 空值补充上0
df3 = df.fillna(0)
# 提取出日期
df3['日期']= df3['RecordTime'].dt.strftime('%d')
# 绘图
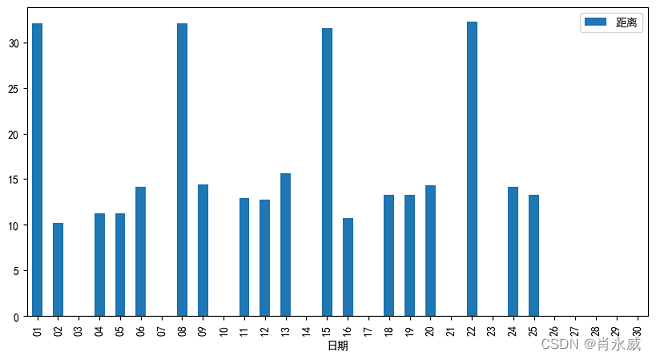
df3.loc[df3['RecordTime'].dt.strftime('%Y-%m')=='2023-07'].plot.bar(x = '日期',y='距离' , figsize=(10, 5))
plt.show()

通过pandas便捷的绘制出每日跑步距离的柱状图。
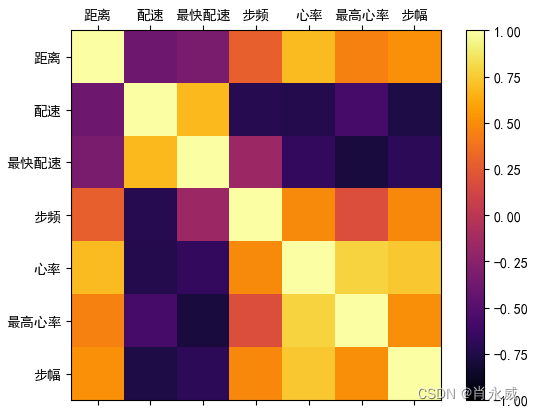
在这里插入图片描述

3.4.2. 复杂的热力图

当使用pandas进行数据分析时，可以使用热力图来可视化相关性矩阵。Pandas模块提供了一个名为corr()的函数（见3.3章节），可用于计算DataFrame中的每个列之间的相关性。热力图使用颜色来表示相关性的强度，从而帮助我们更直观地了解多个变量之间的关系。

import matplotlib.pyplot as plt
import numpy as np

num=111
plt.rcParams['font.sans-serif'] = ['SimHei']     # 设置正常显示中文
plt.rcParams['axes.unicode_minus']=False # 解决不显示负号 
fig = plt.figure() #调用figure创建一个绘图对象
ax = fig.add_subplot(num)

cax = ax.matshow(corr,cmap = 'inferno', vmin=-1, vmax=1)  #绘制热力图，从-1到1
fig.colorbar(cax)  #将matshow生成热力图设置为颜色渐变条
ticks = np.arange(0,len(corr),1) #生成0-9，步长为1
ax.set_xticks(ticks)  #生成刻度
ax.set_yticks(ticks)

feature = corr.columns  # 显示列名
ax.set_xticklabels(feature) #生成x轴标签
ax.set_yticklabels(feature)
plt.show()