前言:
前几次讲了如何构建一个堆以及TopK算法,那么这次给大家分享一下堆排序的两种方法。
方法一
直接暴力解决,建一个小堆,把数组的数据依次push,随后每次Pop堆顶,放进数组里。不过该方法因为建堆有消耗,所以空间复杂度为 O(N)。
步骤:
1.构建小堆
2.把数组里的数据依次Push(添加)进堆里面
3.取堆顶元素,放入数组,随后Pop掉堆顶
构建的小堆
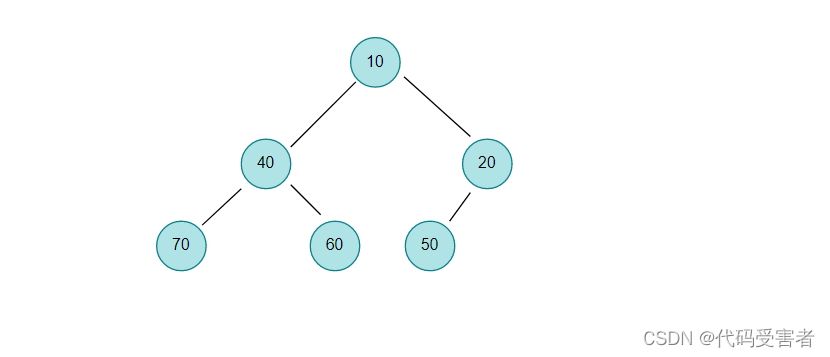
随后取堆顶元素,放入数组,在Pop掉堆顶元素。

代码
//堆排序 方式一
void Heap_Sort1(int* data,int n)
{
//建小堆
HP hp;
HeapInit(&hp);
int i = 0;
for (i = 0; i < n; i++)
{
//依次push
HeapPush(&hp,data[i]);
}
int* tmp = data;
//取每次堆顶元素
while (!HeapEmpty(&hp))
{
//取堆顶
HeapDataType top = HeapTop(&hp);
//放入数组
*tmp = top;
tmp++;
//移除堆顶
HeapPop(&hp);
}
}
排序结果
方法二
当然,我们都知道,建堆是有消耗的。如果我们排序还要建一个堆的话,那么空间复杂度就变成了O(N)。那么接下来就给大家分享一个时间复杂度O(1)的方法。那就是把数组直接变成堆。
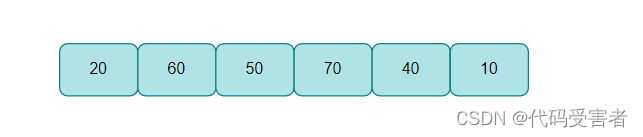
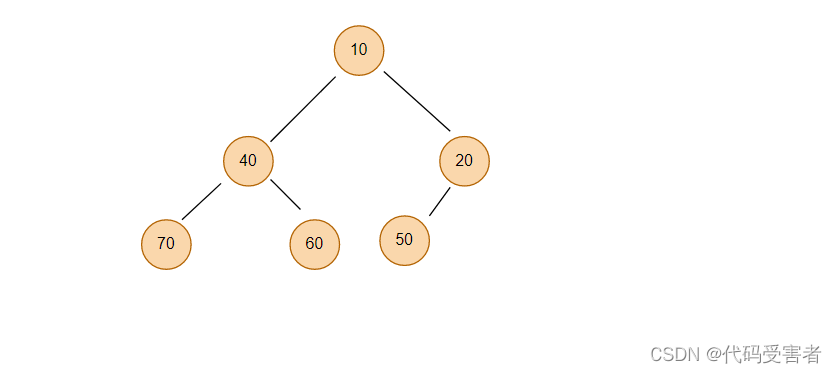
还是这个数组,那么怎么把它构建成堆呢?我们先把它以完全二叉树的形式展现出来。
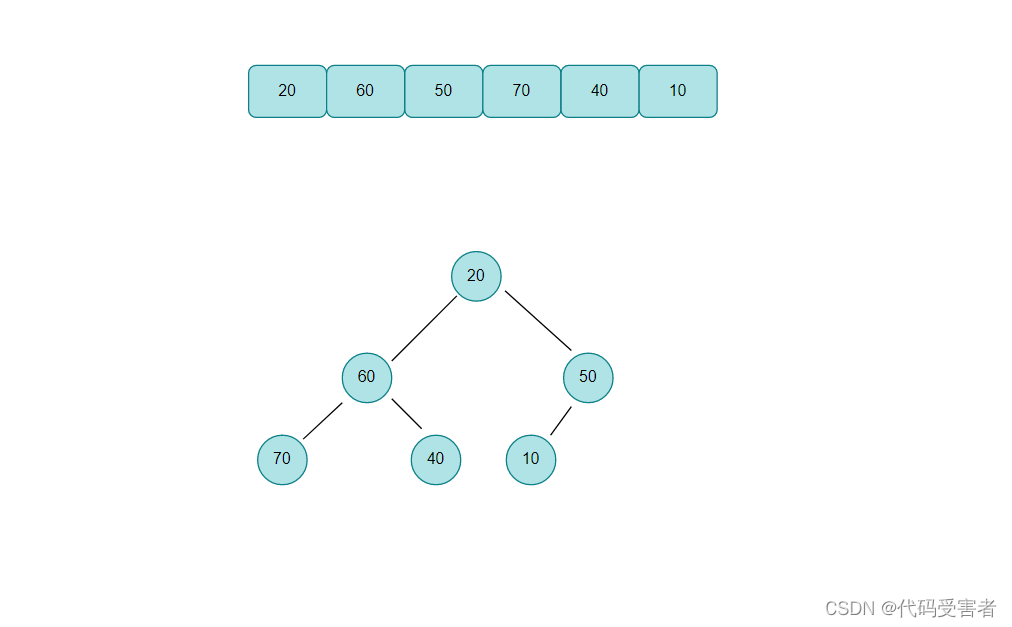
我们可以从倒数第二层开始,随后把它们都看成是一颗子树,依次向下调整。
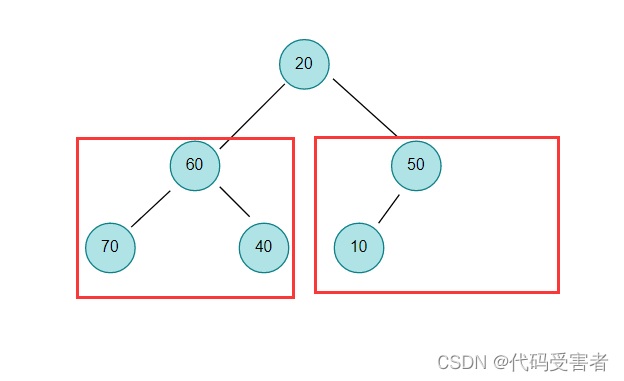
我们先让 50开始向下调整,50比10要大,所以向下调整后,50和10会交换位置。然后60开始向下取整,因为70比40大,所以 60和40对比,60大于40,所以60和40交换位置。最后再往上一层开始继续向下调整。

那么如何找到最后一个父亲呢? 很简单,我们用 (最后一个孩子的小标 - 1 )/2就可以找到最后一个父亲。
所以我们要把数组构建成堆,那就从 (n-1-1) / 2 下标的位置开始依次往前进行向下调整,n为数组的长度。
代码
void Heap_Sort2(int* data, int n)
{
assert(data);
//把数组构建成堆
int TailFather = (n - 1 - 1) / 2; //最后一个父亲
while (TailFather >= 0)
{
//向下调整
AdjustDown(data,n,TailFather);
TailFather--;
}
}
构建成小堆后,我们打印一下。
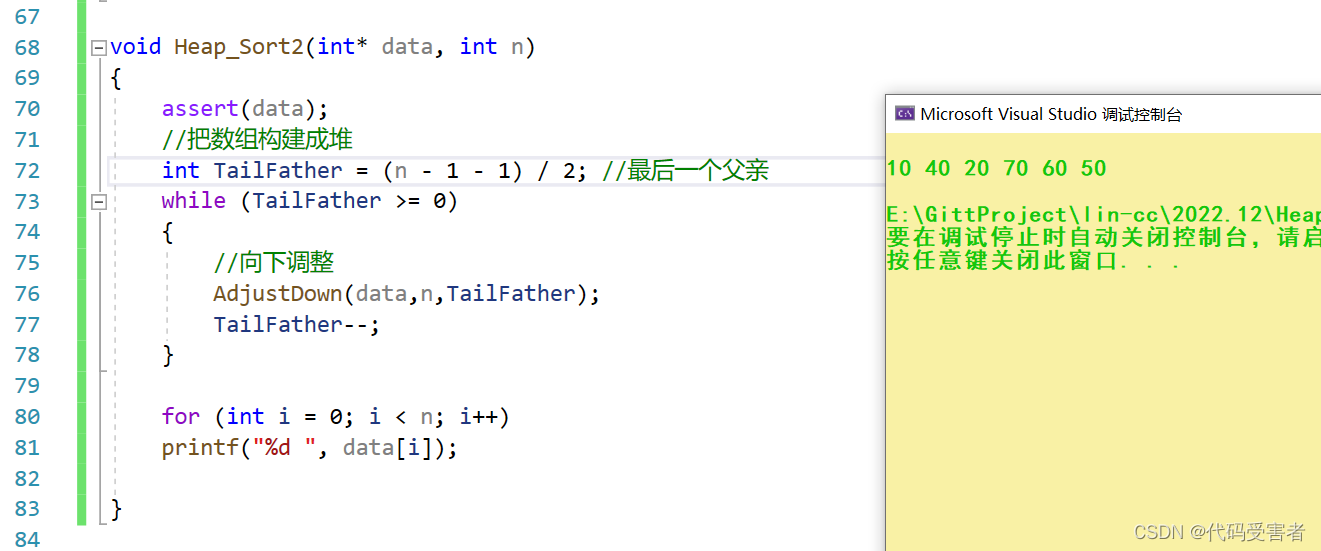
发现和我们图上的顺序是一样的
但是此刻,我们发现这不是有序的,那么我们还要继续调整。
此时我们发现,我们只能找到最小的,但是要找次小的,就非常麻烦。那怎么办呢? 我们排升序的话,可以试试建大堆!那我们来建大堆试试。
改一下向下调整的参数
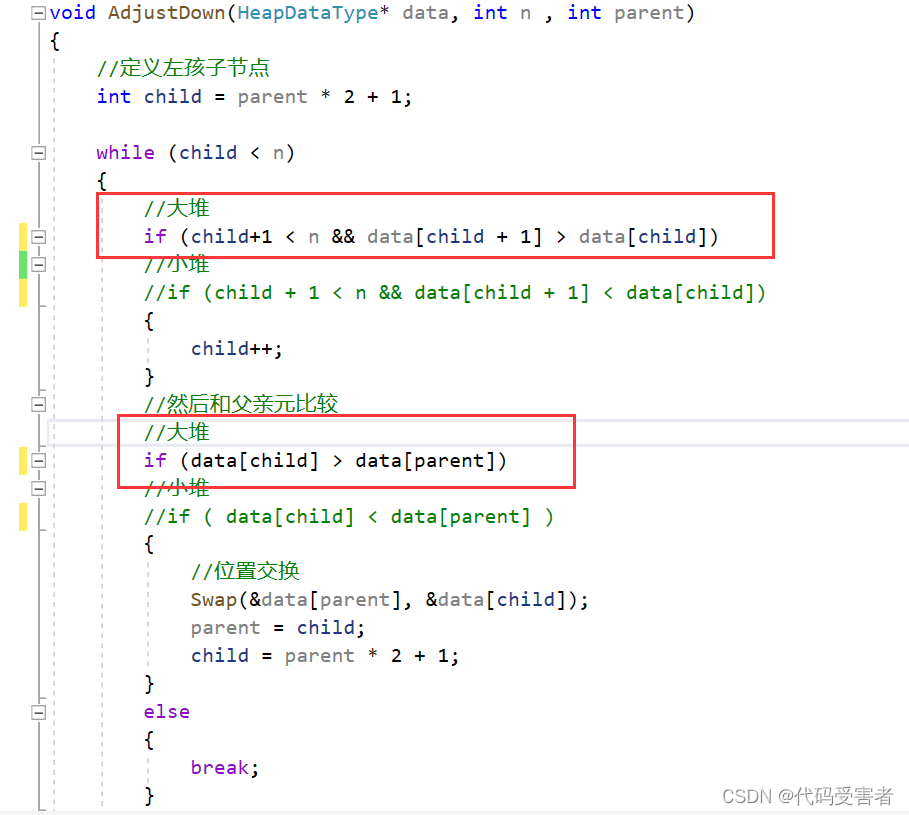
此时数组变成了大堆
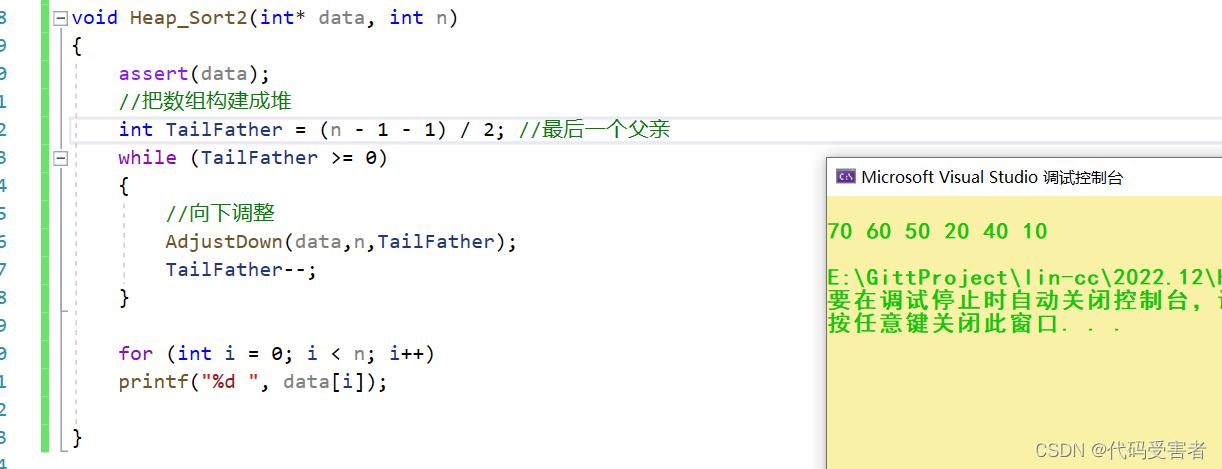
这时候就简单了,我们可以把70和10交换位置,随后把 10 - 40这段距离看成一个堆。
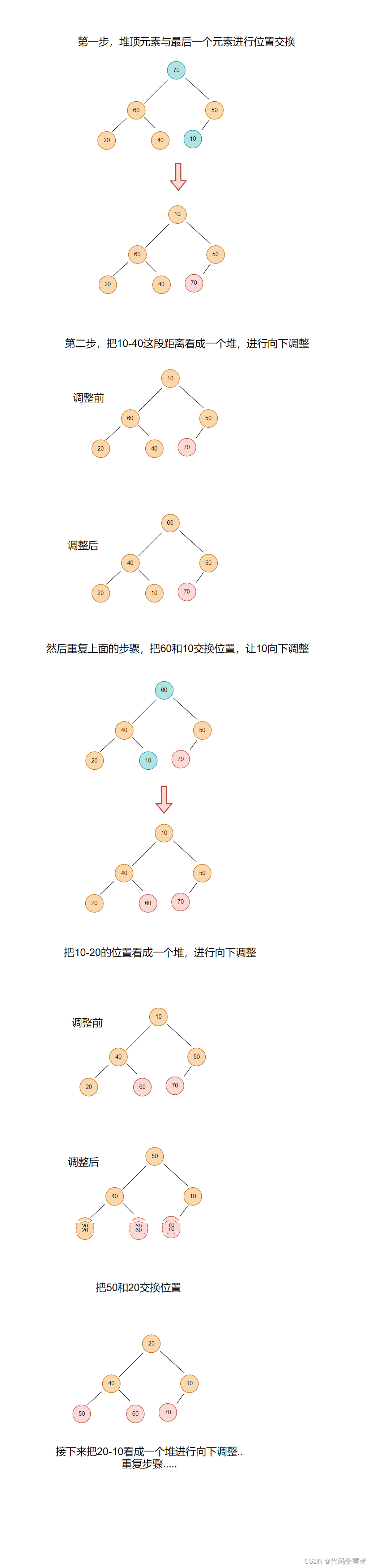
步骤:
1.把数组构建成堆,升序用大堆,降序用小堆。
2.让堆顶元素和最后一个元素进行交换。(不是数组的最后一个元素,而是堆的最后一个元素。)
3.交换完后,让堆顶元素向下取整。
代码
void Heap_Sort2(int* data, int n)
{
assert(data);
//把数组构建成堆
int TailFather = (n - 1 - 1) / 2; //最后一个父亲
while (TailFather >= 0)
{
//向下调整
AdjustDown(data,n,TailFather);
TailFather--;
}
for (int i = 0; i < n; i++)
printf("%d ", data[i]);
printf("\n");
//最后一个元素
int end = n - 1;
while (end >= 0)
{
//交换位置
Swap(&data[0], &data[end]);
//向下取整
AdjustDown(data, end, 0);
end--;
}
}
排序结果

如果我们想排降序呢?很简单,我们建小堆就行了。
只需要向下调整时,我们改成建小堆即可。
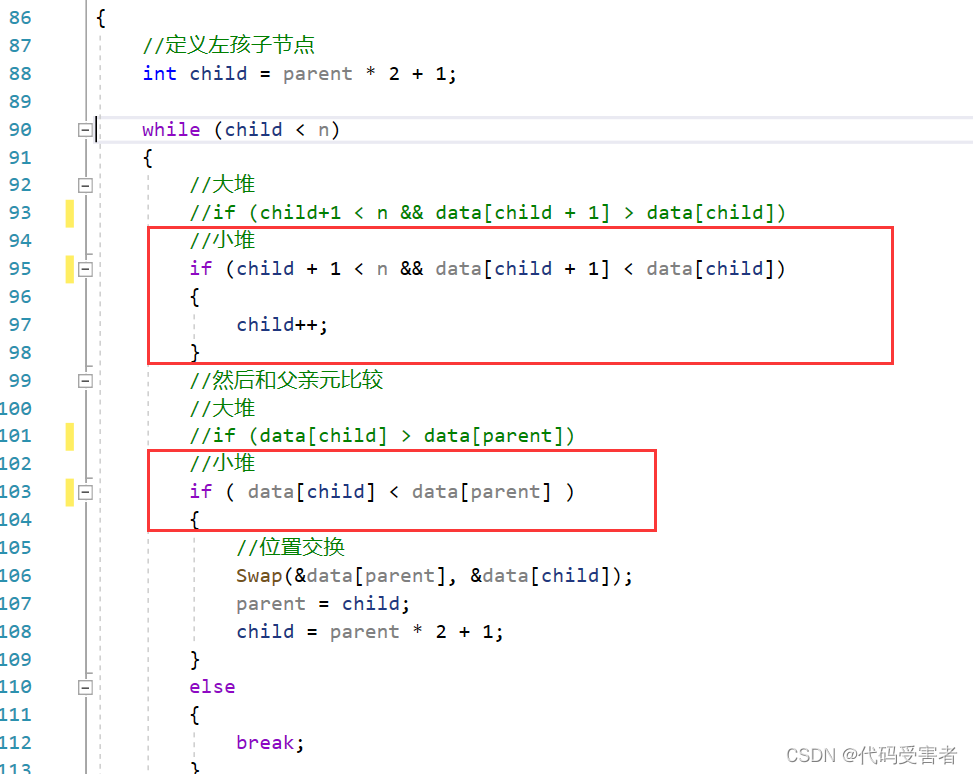
这样我们的降序就排好了
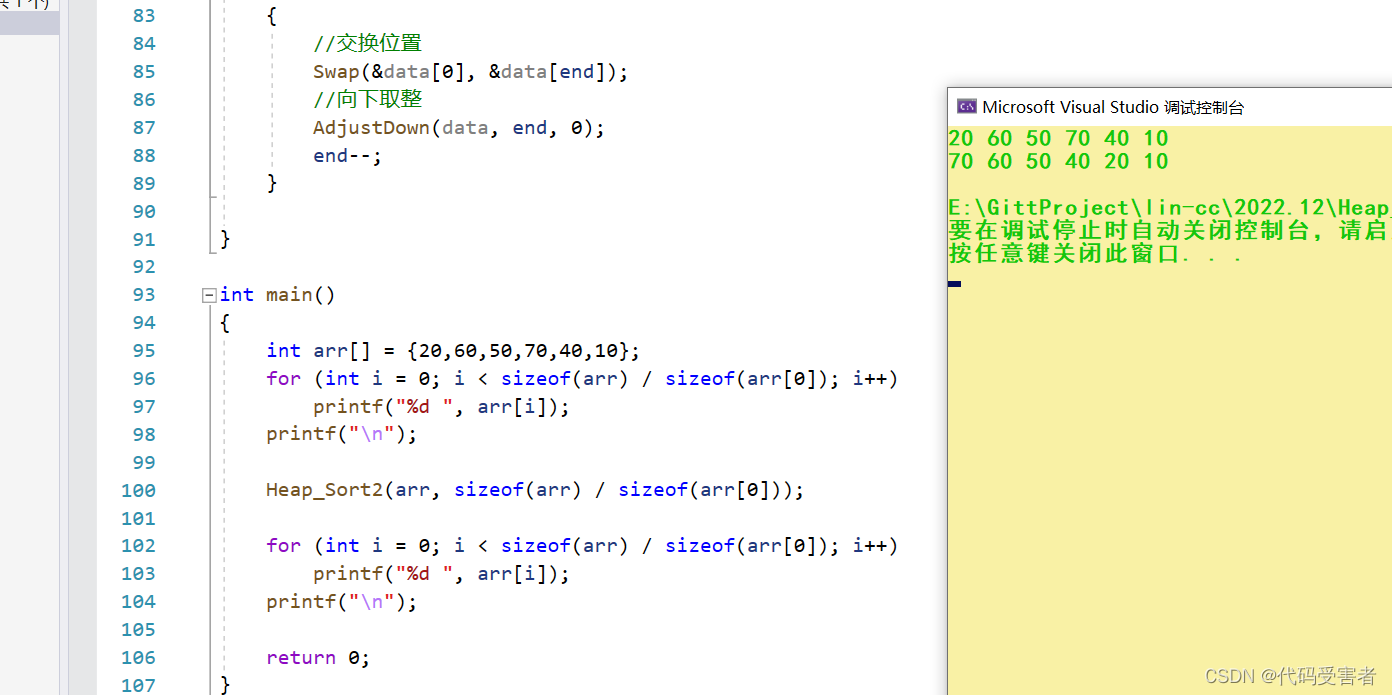
今天的堆排序就到了。
如果不知道堆怎么实现,可以看看我写的这篇文章【数据结构】堆的实现,以及用堆实现的TopK算法TopK问题。
完整代码已上传至git,git链接