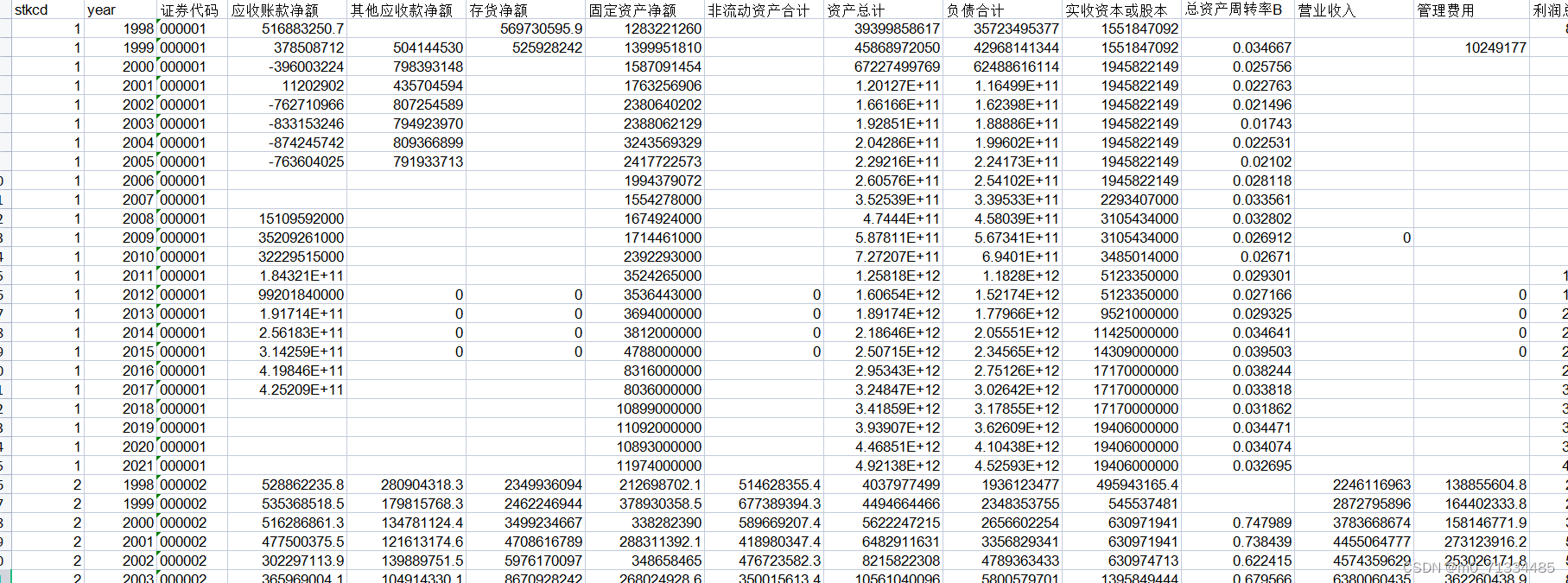
想要数据集请点赞关注收藏后评论区留言留下QQ邮箱
k-means具体是什么这里就不再赘述,详情可以参见我这篇博客
k-means
问题描述:银行对客户信息进行采集,获得了200位客户的数据,客户特征包括以下四个1:社保号码 2:姓名 3:年龄 4:存款数量 使用k-means算法对客户进行分组,生成各类型客户的特点画像
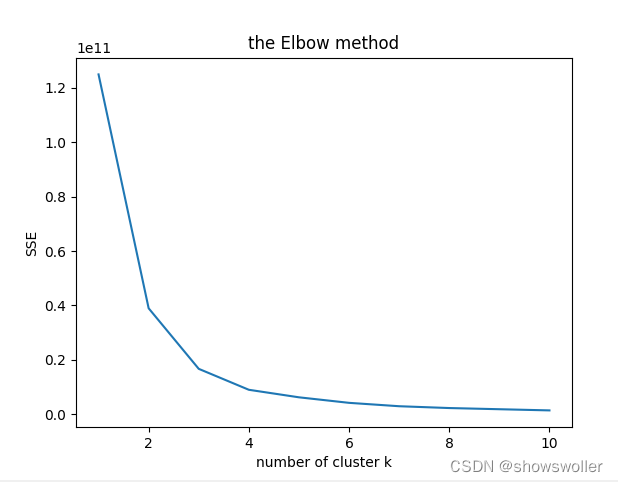
肘部折线图如下 tips:利用肘部方法可以找到最佳的簇数,即看那个点之后逐渐收敛,则那个点为最优的簇数
由下图可以得知k=3或k=4时比较好
分类出的画像图如下,可以清楚的看出不同客户的画像
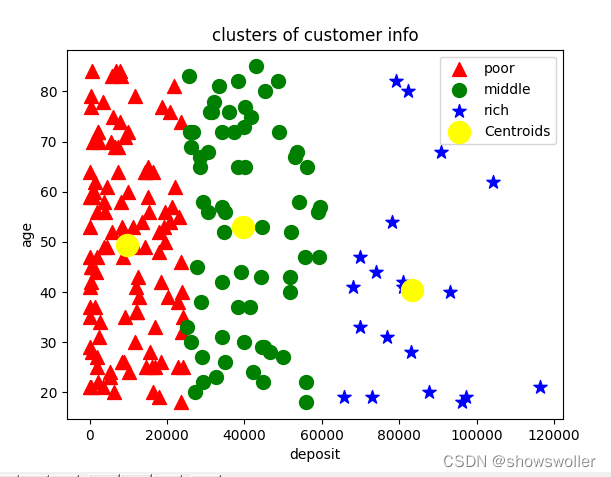
源码如下
#-*-coding:utf-8-*-
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import matplotlib; matplotlib.use('TkAgg')
dataset=pd.read_csv(r'Customer_Info.csv')
print(dataset)
X=dataset.iloc[:,[4,3]].values
from sklearn.cluster import KMeans
sumDs=[]
for i in range(1,11):
kmeans=KMeans(n_clusters=i)
kmeans.fit(X)
sumDs.append(kmeans.inertia_)
print(kmeans.inertia_)
plt.plot(range(1,11),sumDs)
plt.title('the Elbow method')
plt.xlabel('number of cluster k')
plt.ylabel('SSE')
plt.show()
kmenas1=KMeans(n_clusters=3,init='k-means++',max_iter=300,n_init=10,random_state=0)
y_kmeans=kmenas1.fit_predict(X)
plt.scatter(X[y_kmeans==0,0],X[y_kmeans==0,1],s=100,marker='^',c='red',label='poor')
plt.scatter(X[y_kmeans==2,0],X[y_kmeans==2,1],s=100,marker='o',c='green',label='middle')
plt.scatter(X[y_kmeans==1,0],X[y_kmeans==1,1],s=100,marker='*',c='blue',label='rich')
plt.scatter(kmenas1.cluster_centers_[:,0],kmenas1.cluster_centers_[:,1],s=250,c='yellow',label='Centroids')
plt.title('clusters of customer info')
plt.xlabel('deposit')
plt.ylabel('age')
plt.legend()
plt.show()数据集请点赞关注收藏后评论区留下QQ邮箱或者私信博主要