【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

• 将某一个数加上 $x$

• 求出某区间每一个数的和

输入格式

第一行包含两个正整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 个整数，表示一个操作，具体如下：

• 1 x k 含义：将第 $x$ 个数加上 $k$

• 2 x y 含义：输出区间 $[x,y]$ 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

样例 #1

样例输入 #1

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

样例输出 #1

14
16

提示

【数据范围】

对于 $30\%$ 的数据，$1\le n\le 8$，$1\le m\le 10$；
对于 $70\%$ 的数据，$1\le n,m\le 10^4$；
对于 $100\%$ 的数据，$1\le n,m\le 5\times 10^5$。

数据保证对于任意时刻，$a$ 的任意子区间（包括长度为 $1$ 和 $n$ 的子区间）和均在 $[-2^{31},2^{31})$ 范围内。

样例说明：

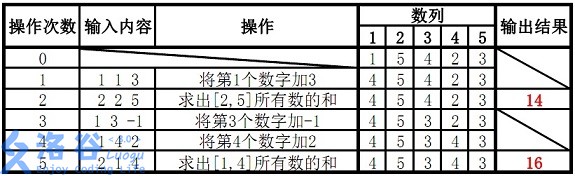
故输出结果14、16

什么是树状数组？

• 树状数组用的是树结构的思想(也就是树型逻辑结构)，而不是真正的“树形结构”
• 具体实现原理如下图
  

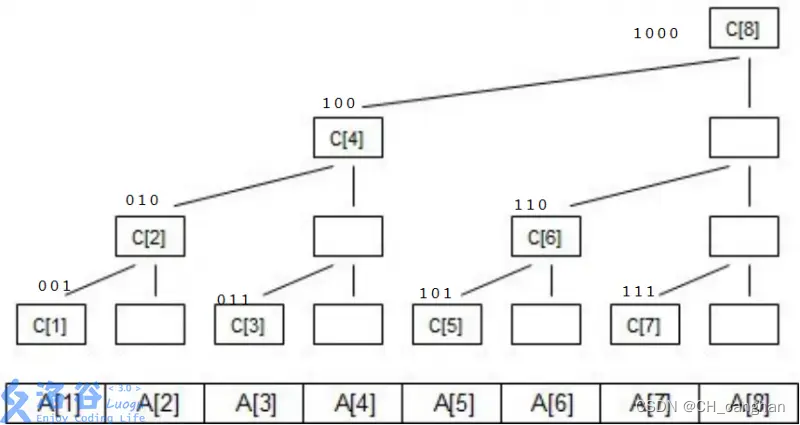
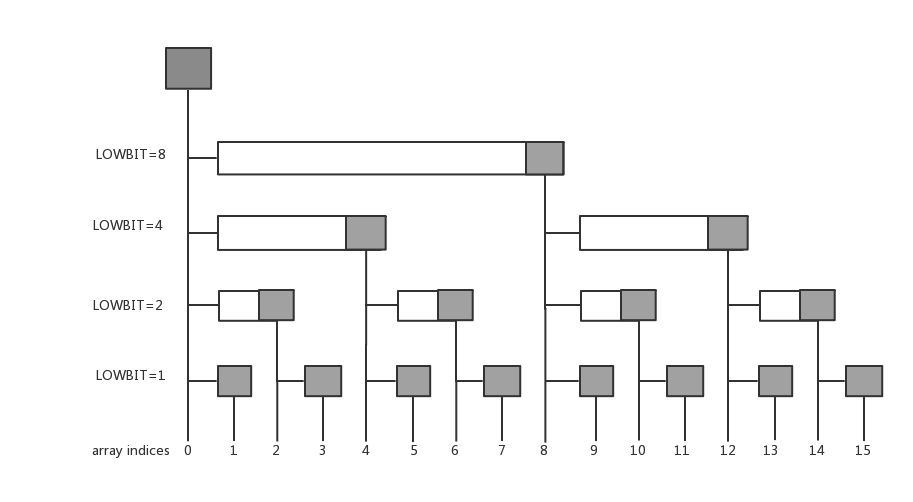
• 而为了实现这样的效果，我们需要一个神奇的二进制转化
  $$lowbit(x)$$
  lowbit 为一个数的二进制表示中最右边 11 所对应的值
  或者说：
  $$lowbit=2^k$$
  ,k为一个数的二进制表示中末尾0的个数
  但实际上还有一种更为简单粗暴的写法
  $$x\&-x$$
  代码实现为

int lowbit(int x){
   return x&-x; 
}

初始化

树状数组的输入也很简单，只需要add( i , a )即可

for(int i=1;i<=n;i++){
		int lk;
		cin>>lk;
		T1.add(i,lk);
	}

单点修改

想要实现在x位置加上ad，在需要修改的部分如图中红线所示

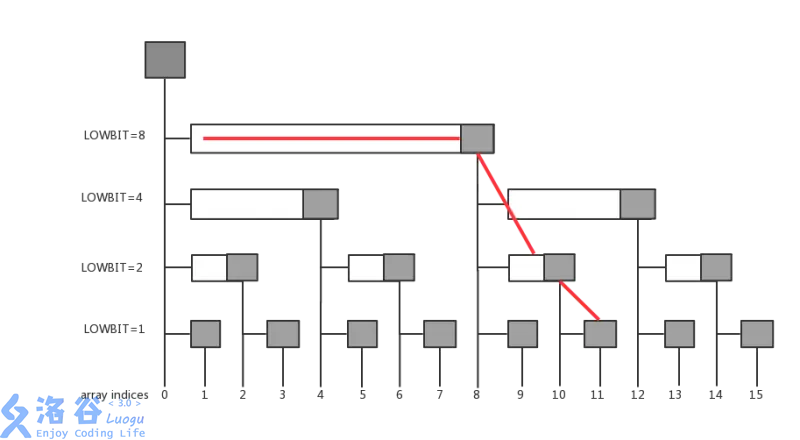
由此我们可以得到以下代码

void add(int x,int ad){
		while(x<=n){
			tr[x]+=ad;
			x+=lowbit(x);
		}
	}

区间查询

树状数组是无法实现直接的区间查询的，它是通过前缀和加减的形式求出的区间和，代码实现如下

int query(int x){
		int ans=0;
		while(x){
			ans+=tr[x];
			x-=lowbit(x);
		}
		return ans;
	}

就这么简单，没了，线段树你*************

能力有限讲的可能并不清楚www

结构体封装

对于树状数组，我们可以把它封装在一个结构体内，代码实现如下

struct bit_tree{
	int tr[N];
	void add(int x,int ad){
		while(x<=n){
			tr[x]+=ad;
			x+=lowbit(x);
		}
	}
	int query(int x){
		int ans=0;
		while(x){
			ans+=tr[x];
			x-=lowbit(x);
		}
		return ans;
	}
}t1;

当然，写函数也是可行的，二者均可

AC CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long int
const int N=1e6+233;
int n,m,a[N];
int lowbit(int x){
	return x&-x; 
}
struct bit_tree{
	int t[N];
	void add(int x,int ad){
		while(x<=n){
			t[x]+=ad;
			x+=lowbit(x);
		}
	}
	int query(int x){
		int ans=0;
		while(x>0){
			ans+=t[x];
			x-=lowbit(x);
		}
		return ans;
	}
}T1;
signed main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		int lk;
		cin>>lk;
		T1.add(i,lk);
	}
	while(m--){
		int op,xx,yy,kk;
		cin>>op;
		if(op==1){
			cin>>xx>>kk;
			T1.add(xx,kk);
		}
		if(op==2){
			cin>>xx>>yy;
			int ans=T1.query(yy)-T1.query(xx-1);
			cout<<ans<<endl;
		}
	}
	return 0;
}

附封面（屑魔女）