目录

一、何谓递归

1.1 计算一列数之和

1.2 递归三原则

1.3 将整数转换成任意进制的字符串

二、栈帧：实现递归

三、递归可视化

四、谢尔平斯基三角形

五、复杂的递归问题

六、动态规划

---

一、何谓递归

递归是解决问题的一种办法，它将问题不断地分成更小的子问题，直到子问题可以用普通的方法解决。

1.1 计算一列数之和

假设需要计算数字列表[1,3,5,7,9]的和。

循环求和函数如下：

def listsum(numList):
    theSum=0
    for i in numList:
        theSum=theSum+i
    return theSum

递归求和函数如下：（递归调用）

def listsum(numList):
    if len(numList)==1:
        return numList[0]
    else:
        return numList[0]+listsum(numList[1:])

1.2 递归三原则

所有的递归算法都要遵守的三个重要原则如下：
（1）递归算法必须有基本情况；

（2）递归算法必须改变其状态并向基本情况靠近；

（3）递归算法必须递归地调用自己。

基本情况是指使算法停止递归的条件，这通常是小到足以直接解决的问题。

为了遵守第二条原则，必须设法改变算法的状态，从而使其向基本情况靠近。改变状态是指修改算法所用的某些数据，这通常意味着代表问题的数据以某种方式变得更小。

最后一条原则是递归算法必须对自身进行调用。

1.3 将整数转换成任意进制的字符串

利用递归将整数转换成以2~16为进制基数的字符串的代码如下：

def toStr(n,base):
    converString="0123456789ABCDEF"
    if n<base:
        return converString[n]
    else:
        return toStr(n//base,base)+converString[n%base]

二、栈帧：实现递归

假设不拼接递归调用toStr的结果和converString的查找结果，而是在进行递归调用之前把字符串压入栈中。

rStack=Stack()

def toStr(n,base):
    converString="0123456789ABCDEF"
    if n<base:
        rStack.push(converString[n])
    else:
        rStack.push(converString[n%base])
        toStr(n//base,base)

当调用函数时，Python分配一个栈帧来处理该函数的局部变量。当函数返回时，返回值就在栈的顶端，以供调用者访问。

栈帧限定了函数所用变量的作用域。尽管反复调用相同的函数，但是每一次调用都会为函数的局部变量创建新的作用域。

三、递归可视化

我们将使用Python的turtle模块来绘制图案。

使用turtle模块绘制螺旋线的代码如下。先导入turtle模块，然后创建一个小乌龟对象，同时也会创建用于绘制图案的窗口。接下来定义drawSpiral函数。这个简单函数的基本情况是，要画的线的长度（参数len）降为0。如果线的长度大于0，就让小乌龟向前移动len个单位距离，然后向右转90度。递归发生在用缩短后的距离再一次调用drawSpiral函数时。在结尾处调用了myWin.exitonclick()函数，这使小乌龟进入等待模式，直到用户在窗口内再次点击之后，程序清理并退出。

from turtle import *

myTurtle=Turtle()
myWin=myTurtle.getscreen()

def drawSpiral(myTurtle,lineLen):
    if lineLen>0:
        myTurtle.forward(lineLen)
        myTurtle.right(90)
        drawSpiral(myTurtle,lineLen-5)

drawSpiral(myTurtle,100)
myWin.exitonclick()

接下来绘制一颗分形树。分形是数学的一个分支，它与递归有很多共同点。分形的定义是，不论放大多少倍来观察分形图，它总是有相同的基本形状。

 绘制分形图的代码如下：

def tree(branchLen,t):
    if branchLen>5:
        t.forward(branchLen)
        t.right(20)
        tree(branchLen-15,t)
        t.left(40)
        tree(branchLen-10,t)
        t.right(20)
        t.backward(branchLen)

from turtle import *
t=Turtle()
myWin=t.getscreen()
t.left(90)
t.up()
t.backward(300)
t.down()
t.color('green')
tree(110,t)
myWin.exitonclick()

四、谢尔平斯基三角形

from turtle import *

def drawTriangle(points,color,myTurtle):
    myTurtle.fillcolor(color)
    myTurtle.up()
    myTurtle.goto(points[0])
    myTurtle.down()
    myTurtle.begin_fill()
    myTurtle.goto(points[1])
    myTurtle.goto(points[2])
    myTurtle.goto(points[0])
    myTurtle.end_fill()

def getMid(p1,p2):
    return ((p1[0]+p2[0])/2,(p1[1]+p2[1])/2)

def sierpinski(points,degree,myTurtle):
    colormap=['blue','red','green','white','yellow','violet','orange']
    drawTriangle(points,colormap[degree],myTurtle)
    if degree>0:
        sierpinski([points[0],getMid(points[0],points[1]),getMid(points[0],points[2])],degree-1,myTurtle)
        sierpinski([points[1], getMid(points[0], points[1]), getMid(points[1], points[2])], degree - 1, myTurtle)
        sierpinski([points[2], getMid(points[2], points[1]), getMid(points[0], points[2])], degree - 1, myTurtle)

myTurtle=Turtle()
myWin=myTurtle.getscreen()
myPoints=[(-500,250),(0,500),(500,-250)]
sierpinski(myPoints,5,myTurtle)
myWin.exitonclick()

五、复杂的递归问题

汉诺塔问题

假设一共有三根柱子，第一根柱子起初有5个盘子，任务是将5个盘子从一根柱子移动到另一根柱子，同时有两个重要的限制条件：每次只能移动一个盘子，并且大盘子不能放在小盘子之上。

如果我们知道如何把上面4个盘子移动到第二根柱子上，那么久轻易地把最底下的盘子移动到第三根柱子上，然后将4个盘子从第二根柱子移动到第三根柱子。但是如果不知道如何移动4个盘子，该怎么办呢？如果我们知道如何把上面的3个盘子移动到第三根柱子上，那么就轻易地把第4个盘子移动到第二根柱子上，然后再把3个盘子从第三个柱子上移动到第二根柱子上。但是如果不知道如何移动3个盘子，该怎么办呢？移动两个盘子到第二根柱子上，然后把第3个盘子移动到第三个柱子上，最后把两个盘子移过来，怎么样？但是如果还是不知道如何移动两个盘子，该怎么办呢？把一个盘子移动到第三个柱子并不难，甚至太简单了。这看上去就是这个问题的基本情况。

以下概述如何借助一根中间柱子，将高度为height的一叠盘子从起点柱子移到终点柱子：

（1）借助终点柱子，将高度为height-1的一叠盘子移到中间柱子；

（2）将最后一个盘子移到终点柱子；

（3）借助起点柱子，将高度为height-1的一叠盘子从中间柱子移到终点柱子。

def moveTower(height,fromPole,toPole,withPole):
    if height>=1:
        moveTower(height-1,fromPole,withPole,toPole)
        moveDisk(fromPole,toPole)
        moveTower(height-1,withPole,toPole,fromPole)

def moveDisk(fp,tp):
    print("moving disk from %d to %d\n"%(fp,tp))

汉诺塔问题的详细讲解（python版）https://blog.csdn.net/wistonty11/article/details/123563309

六、动态规划

在解决优化问题时，一个策略是动态规划。

优化问题的一个经典例子就是在找零时使用最少的硬币。假设某个自动售货机制造商希望在每笔交易中给出最少的硬币。一个顾客使用一张一美元的纸币购买了价值37美元的物品，最少需要找给该顾客多少硬币呢？答案是6枚：25美分的2枚，10美分的1枚，1美分的3枚。该如何计算呢？从面值最大的硬币（25美分）开始，使用尽可能多的硬币，然后尽可能地使用面值第2大的硬币。这种方法叫做贪婪算法——试图最大程度地解决问题。

算法基础：贪婪算法（基于Python）https://blog.csdn.net/leowinbow/article/details/88140107让我们来考察一种必定能得到最优解的方法。这是一种递归方法。首先确定基本情况：如果要找的零钱金额与硬币面值相同，那么只需找1枚硬币即可。

如果要找的零钱硬币和硬币的面值不同，则有多种选择：1枚1分的硬币加上找零钱金额减去1分之后所需的硬币；1枚5分的硬币加上找零金额减去5分之后所需的硬币；1枚10分的硬币加上找零金额减去10分之后所需的硬币；1枚25分的硬币加上找零金额减去25分之后所需的硬币。我们需要从中找到硬币数最少的情况，如下所示：

numCoins=min(1+numCoins(originalamount-1),1+numCoins(originalamount-5),1+numCoins(originalamount-10),1+numCoins(originalamount-20))

找零问题的递归解决方案如下：

def recMC(coinValueList,change):
    minCoins=change
    if change in coinValueList:
        return 1
    else:
        for i in [c for c in coinValueList if c<=change]:
            numCoins=1+recMC(coinValueList,change-i)
            if numCoins<minCoins:
                minCoins=numCoins
    return minCoins

recMC([1,5,10,25],63)

显然，该算法将大量时间和资源浪费在了重复计算已有的结果上。

减少计算量的关键在于记住已有的结果。简单的做法是把最少硬币数的计算结果存储在一张表中，并在计算新的最少硬币数之前，检查结果是否已在表中。如果是，就直接使用结果，而不是重新计算。

添加查询表之后的找零算法：

def recDC(coinValueList,change,knownResults):
    minCoins=change
    if change in coinValueList:
        knownResults[change]=1
        return 1
    elif knownResults[change]>0:
        return knownResults[change]
    else:
        for i in [c for c in coinValueList if c<=change]:
            numCoins=1+recDC(coinValueList,change-i,knownResults)
            if numCoins<minCoins:
                minCoins=numCoins
                knownResults[change]=minCoins
    return minCoins

recDC([1,5,10,25],63,[0]*64)

上面所做的优化并不是动态规划，而是通过记忆化（或者叫作缓存）的方法来优化程序的性能。

真正的动态规划算法会用更系统化的方法来解决问题。在解决找零问题时，动态规划算法会从1分找零开始，然后系统地一直计算到所需的找零金额。这样做可以保证在每一步都已经知道任何小于当前值的找零金额所需的最少硬币数。

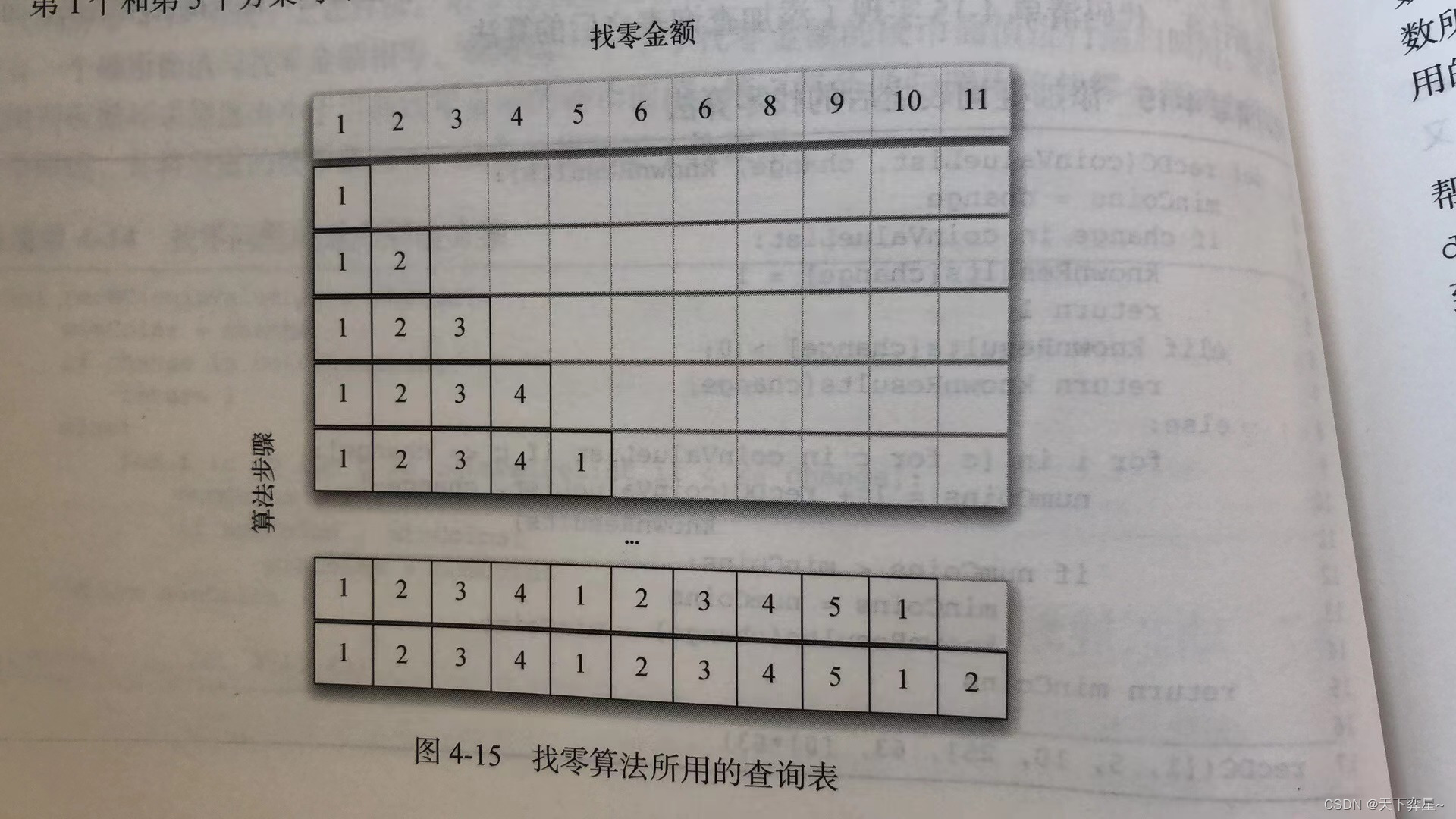
在这个过程中，从1分开始，只需找1枚1分的硬币。第2行展示了1分和2分所需的最少硬币数。同理，2分只需找2枚1分的硬币。第5行开始变得有趣起来，此时我们有2个可选方案：要么找5枚1分的硬币，要么找1枚5分的硬币。哪个方案更好呢？查表后发现，4分所需的最少硬币数是4，再加上1枚1分的硬币就得到5分（共需要5枚硬币）；如果直接找1枚5分的硬币，则最少硬币数是1.由于1比5小，因此我们把1存入表中。接着来看11分的情况，我们有3个可选方案：

（1）1枚1分的硬币加上找10分零钱（11-1）最少需要的硬币（1枚）。

（2）1枚5分的硬币加上找6分零钱（11-5）最少需要的硬币（2枚）。

（3）1枚10分的硬币加上找1分零钱（11-10）最少需要的硬币（1枚）。

第1个和第3个方案均可得到最优解，即共需要2枚硬币。

找零问题的动态规划解法代码如下所示。dpMakeChange接受3个参数：硬币面值列表、找零金额，以及由每一个找零金额所需的最少硬币数构成的列表。当函数运行结束时，minCoins将包含找零金额从0到change的所有最优解。

def dpMakeChange(coinValueList,change,minCoins):
    for cents in range(change+1):
        coinCount=cents
        for j in [c for c in coinValueList if c<=cents]:
            if minCoins[cents-j]+1<coinCount:
                coinCount=minCoins[cents-j]+1
        minCoins[cents]=coinCount
    return minCoins[change]

dpMakeChange并不是递归函数。

修改后的动态规划解法：
 

def dpMakeChange(coinValueList,change,minCoins,coinsUsed):
    for cents in range(change+1):
        coinCount=cents
        newCoin=1
        for j in [c for c in coinValueList if c<=cents]:
            if minCoins[cents-j]+1<coinCount:
                coinCount=minCoins[cents-j]+1
                newCoin=j
        minCoins[cents]=coinCount
        coinsUsed[cents]=newCoin
    return minCoins[change]

def printCoins(coinsUsed,change):
    coin=change
    while coin>0:
        thisCoin=coinsUsed[coin]
        print(thisCoin)
        coin=coin-thisCoin

cl=[1,5,10,21,25]
coinsUsed=[0]*64
coinCount=[0]*64
dpMakeChange(cl,63,coinCount,coinsUsed)
print(printCoins(coinsUsed,63))
print(printCoins(coinsUsed,52))
print(coinsUsed)

运行结果如下：

21
21
21
None
10
21
21
None
[1, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 1, 1, 1, 1, 5, 1, 1, 1, 1, 10, 21, 1, 1, 1, 25, 1, 1, 1, 1, 5, 10, 1, 1, 1, 10, 1, 1, 1, 1, 5, 10, 21, 1, 1, 10, 21, 1, 1, 1, 25, 1, 10, 1, 1, 5, 10, 1, 1, 1, 10, 1, 10, 21]

动态规划（Dynamic programming）详解https://blog.csdn.net/qq_37771475/article/details/126855564