摘要
多模态学习通过整合不同的感官,有助于全面理解世界。因此,多种输入模式有望提高模型的性能,但我们实际上发现,即使多模态模型优于其单模态模型,它们也没有得到充分利用。具体地说,在本文中,我们指出现有的多模态鉴别模型,即为所有模态设计统一的目标,在某些情况下,可能保持欠优化的单模态表示,如吹风事件中的声音,绘画事件中的视觉等。为了缓解这种优化不平衡,我们提出了动态梯度调制,通过监测它们对学习目标的贡献的差异,自适应地控制每个模态的优化。此外,还引入了一个动态变化的额外高斯噪声,以避免梯度调制可能引起的泛化下降。因此,在不同的多模态任务上,我们比常见的融合方法取得了相当大的改进,这种简单的策略也可以提高现有的多模态方法,这说明了它的有效性和多功能性。
介绍
人们通过协同利用多种感官来感知世界:眼睛看,耳朵听,手触摸。这种多模式的方式可以从不同的方面提供更全面的信息。受人类的多感官整合能力的启发,从不同传感器收集的多模态数据在机器学习中更容易被考虑。近年来,多模态学习在提高以往单模态任务的性能以及解决动作识别、视听语音识别、视觉问答等新的挑战性问题方面表现出了明显的优势。与单模态数据相比,多模态数据通常提供更多的视图,因此使用多模态数据的学习应该匹配或优于单模态情况。然而,根据最近的研究,在某些情况下,优化所有联合训练策略的统一学习目标的多模态模型可能不如单峰模型。这种现象违反了通过整合来自多种模式的信息来提高模型性能的意图。以往的研究人员声称,不同的模式倾向于以不同的速度收敛,导致不协调收敛问题。为了解决这一问题,一些方法利用额外的单模态分类器或预先训练好的模型来帮助训练多模态模型。因此,它们不可避免地需要额外地训练额外的神经模块。
然而,我们进一步发现,即使多模态模型优于单模态模型,它们仍然不能充分利用多种模态的潜力。
如图1所示,联合多模态模型在VGGSsound上取得了最好的事件分类性能,但其视觉和音频模态的性能明显分别低于仅视觉模型和仅音频模型1。这一有趣的观察结果表明,这两种模式的表现都优化不足。我们认为原因可能是,在一些多模态场景中,主导的具有更好的性能(例如,风声,踢足球的视觉等)。会抑制另一个人的优化。
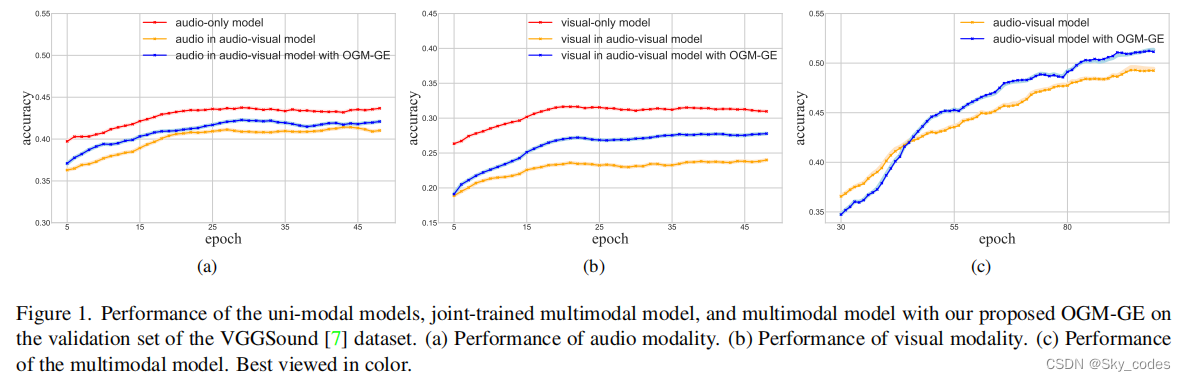
此外,如图1(a)和(b)所示,还有另一个明显的观察精度下降更明显的视觉模式与音频情况相比,这与VGGSound,作为一个策划声音数据集,更喜欢音频模式,甚至声源保证是可见的。一般来说,这样的数据集偏好会导致一种模态通常占主导地位,从而导致这种优化不平衡的现象。为了解决上述问题,我们首先从优化的角度分析了不平衡现象,发现性能较好的模态有助于降低联合鉴别损失,然后通过在其他模态上传播有限的梯度来主导优化过程,从而导致优化不足的情况。然后,为了缓解这种情况,我们提出通过动态梯度调制(OGM)策略来控制每个模态的优化过程。具体来说,在训练过程中,动态监测不同模态对学习目标的贡献差异,然后利用其自适应地调节梯度,为优化不足的模态提供更多的努力。然而,调制后的梯度可以降低随机梯度噪声的强度,这已被证明与泛化能力呈正相关。因此,我们进一步引入了动态变化的额外高斯噪声来实现泛化增强(GE)。将我们的OGM-GE方法应用于图1中VGGSsound的多模态学习任务后,我们得到了未充分优化的单模态表示的一致性能提升,即图1(a)和(b).中的蓝色曲线。更重要的是,视觉形态获得了更多的改进。因此,我们的方法在多模态学习设置中明显优于传统的方法,如图1©.所示。为了全面证明OGM-GE的有效性,我们在不同数据集上的各种多模态任务中测试了它,这带来了一致的改进,同时使用普通融合策略和现有的多模态方法。
综上所述,我们的贡献如下:
- 我们发现联合多模态模型的性能限制了联合多模态模型的优化不平衡现象,然后从优化的角度对其进行了分析。
- 提出了该方法,通过动态控制各模态的优化过程,提高泛化能力来解决优化不平衡问题。
- 所提出的OGM-GE不仅可以插入普通的融合策略,还可以插入现有的多模态框架,并带来持续的改进,表明其很有前途的多功能性。
相关工作
Multimodal learning
Imbalanced multimodal learning
Stochastic gradient noise
认为SGD的梯度噪声与深度模型的泛化能力有重要的相关性。这种随机梯度噪声是通过随机小批量抽样引入的,被认为是一种正则化方法,帮助模型摆脱鞍点或局部最优。Zhou等人进一步提供了理论证明,证明随机梯度算法结合适当的高斯噪声,保证通过随机初始化在多项式时间内收敛到全局最优。在本工作中,为了提高多模态模型的生成能力,我们在梯度中引入了额外的高斯噪声,并取得了相当大的改进。
方法
Optimization imbalance analysis
通过对优化不平衡现象的分析,发现多模态模型的优化过程主要由性能较好的模态所主导,导致另一种模态的优化不足。这里我们以音频和视觉模式为例。为方便起见,我们表示训练数据集 D = { x i , y i } i = 1 , 2... N D = \{x_i,y_i\}_{i=1,2...N} D={xi,yi}i=1,2...N。每个xi由两个来自不同模式的两个输入组成,如 x i = ( x i a , x i v ) x_i=(x^a_i,x^v_i) xi=(xia,xiv),其中a和v分别表示音频和视觉模式。 y i ∈ { 1 , 2 , ⋅ ⋅ ⋅ , M } y_i∈\{1,2,···,M\} yi∈{1,2,⋅⋅⋅,M},其中,M是类别的数量。我们使用两个编码器 φ a ( θ a , ⋅ ) φ^a(θ^a,·) φa(θa,⋅)和 φ v ( θ v , ⋅ ) φ^v(θ^v,·) φv(θv,⋅)来提取特征,其中 θ a θ^a θa和 θ v θ^v θv是编码器的参数。例如,我们以最广泛使用的普通融合方法,连接,作为例子2。设 W ∈ R M × ( d φ a + d φ v ) W∈R^{M×(d_{φa}+d_{φv})} W∈RM×(dφa+dφv)和 b ∈ R M b∈R^M b∈RM表示最后一个线性分类器的参数。然后,多模态模型的对数输出如下:
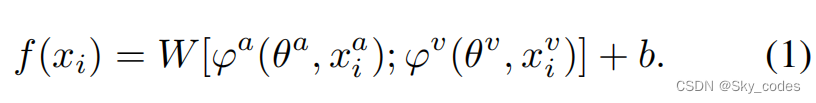
为了单独观察每个模态的优化过程,W可以表示为两个块的组合:$ [Wa,Wv ]$。方程1可以改写为:
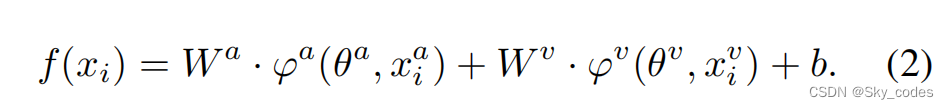
我们将类c的logits输出表示为
f
(
x
i
)
c
f(x_i)_c
f(xi)c,而判别模型的交叉熵损失变为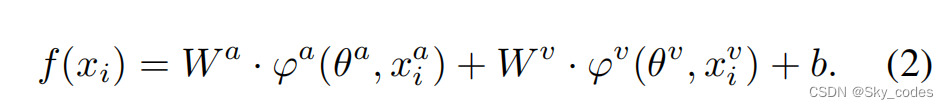
使用梯度下降(GD)优化方法, W a W^a Wa和编码器 φ a ( θ a , ⋅ ) φ^a(θ^ a,·) φa(θa,⋅)的参数更新为(类似于 W v W^v Wv和 φ v ( θ v , ⋅ ) φ^ v(θ^ v,·) φv(θv,⋅)):
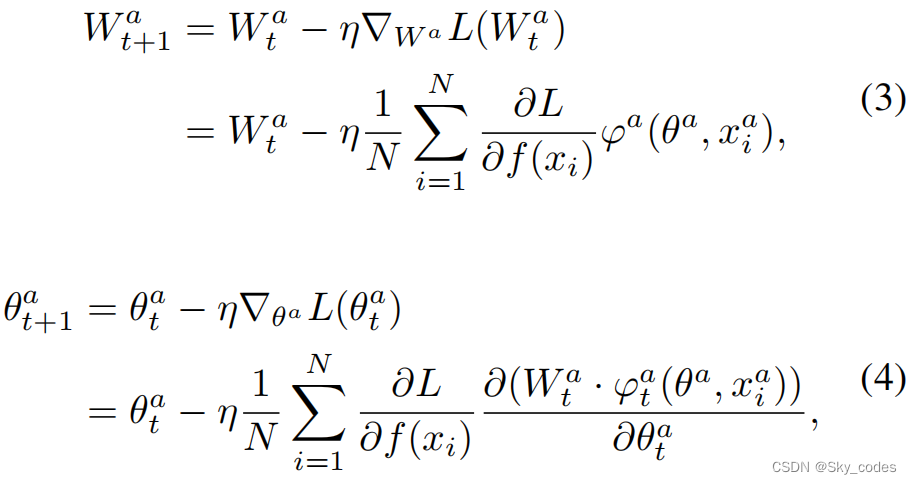
其中,η为学习率。根据公式3和公式4,我们可以发现 W a W^a Wa和 φ a φ^a φa的优化除了与训练损失 ∂ L / ∂ f ( x i ) ∂L/∂f(x_i) ∂L/∂f(xi)相关的优化外,与其他模态的优化几乎没有相关性。因此,单模态编码器很难根据彼此之间的反馈进行调整。然后结合方程2,梯度 ∂ L / ∂ f ( x i ) ∂L/∂f(x_i) ∂L/∂f(xi)可以重写为:
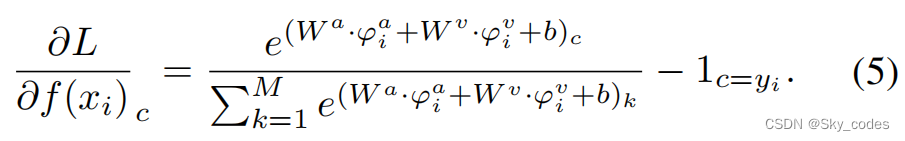
为了方便起见,我们将 φ a ( θ a , ⋅ ) φ^a(θ^ a,·) φa(θa,⋅)和 φ v ( θ v , ⋅ ) φ^ v(θ^ v,·) φv(θv,⋅)分别简化为 φ i a φ^a_i φia和 φ i v φ^v_ i φiv。然后,我们可以推断,对于属于 y i y_i yi类的样本 x i x_i xi,当一种模态,如视觉模态,具有更好的性能时,它通过 W v ⋅ φ i v W^v·φ^ v_ i Wv⋅φiv对 ∂ L / ∂ f ( x i ) y i ∂L/∂f(x_i)_{y_i} ∂L/∂f(xi)yi的贡献更大,从而降低全局损失。因此,音频模态对正确类别相对较低的可信度,可以获得有限的优化努力w.r.t.其在反向传播过程中的模态特定参数。这一现象表明,性能较好的模态在优化过程中占主导地位。因此,当多模态模型的训练即将收敛时,另一种模态仍可能出现表示优化不足的情况,需要进一步的训练。
On-the-fly gradient modulation
如前所述,多模态判别模型的优化过程通常以性能较好的模态为主导,导致表示优化不足,限制了模型的性能。为了解决这个问题,我们的目标是通过OGM策略来修改每个模态的优化过程,如图2所示。
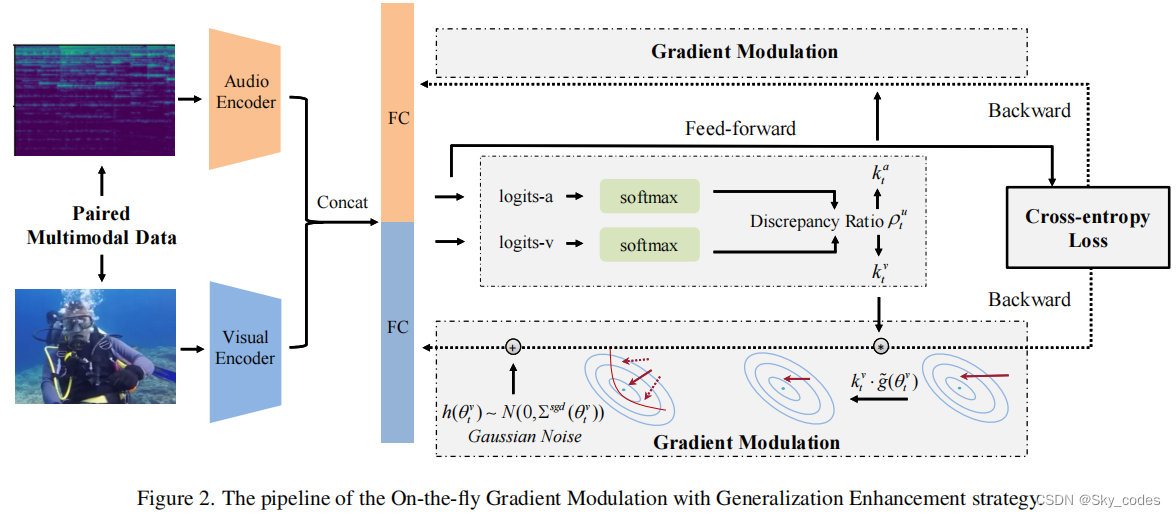
在本节中,我们将遵循第3.1节中的符号。编码器 φ u φ^u φu的参数 θ u θ^u θu,其中 u ∈ { a , v } u∈\{a,v\} u∈{a,v},更新如下:
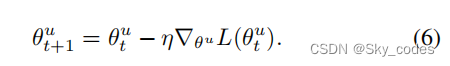
在实际应用中,我们采用了广泛使用的随机梯度下降(SGD)优化方法,并将参数更新为:
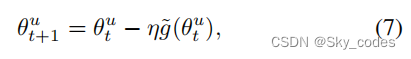
其中, g ˜( θ u t ) = 1 / m Σ x ∈ B t ∇ θ u ℓ ( x ; θ u t ) g˜(θ^t_ u)=1/mΣ_{x∈B_t}∇{θ^u}ℓ(x;θ^t_ u) g˜(θut)=1/mΣx∈Bt∇θuℓ(x;θut)是对全梯度 ∇ θ u L ( θ t u ) ∇_{θ^u} L(θ^ u_ t) ∇θuL(θtu)的无偏估计。 B t B_t Bt是一个随机的小批,在第t步中选择,大小为m, ∇ θ u ℓ ( θ t u ) ∇_{θ^u} ℓ(θ^ u_ t) ∇θuℓ(θtu)是梯度w.r.t. B t B_t Bt.
针对第3.1节中讨论的优化不平衡问题,我们建议通过监测每个模态对学习目标的贡献的差异,来自适应地调制每个模态的梯度。这里我们设计了差异比 ρ t u ρ ^u_ t ρtu:
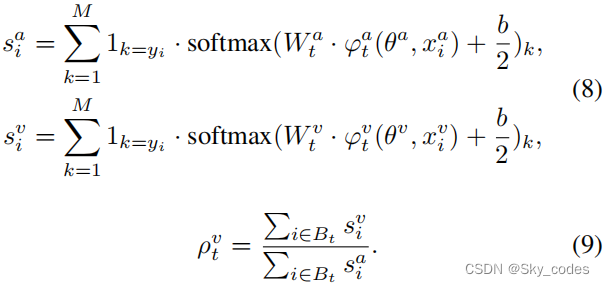
ρ
t
a
ρ^ a_ t
ρta因此被定义为
ρ
t
v
ρ^ v_ t
ρtv的倒数。这里我们使用
(
W
i
u
⋅
φ
i
(
θ
u
,
x
i
u
)
+
b
/
2
)
(W_i^ u·φ_i(θ^ u,x^u_ i)+ b/ 2)
(Wiu⋅φi(θu,xiu)+b/2)作为模态u的近似预测,来估计多模态模型的单模态性能。通过
ρ
t
u
ρ ^u_ t
ρtu来动态监测音频和视觉模式之间的贡献差异,我们能够通过以下方式自适应地调节梯度:
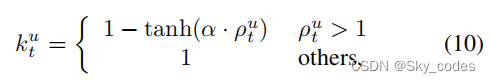
其中,α是用来控制调制程度的一个超参数。我们将系数 k t u k_t^ u ktu整合到SGD优化方法中,迭代t中的 θ t u θ_t^ u θtu更新如下:
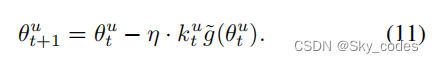
通过 k t u k_t^ u ktu,减轻了性能更好的模态( ρ t u ρ ^u_ t ρtu > 1)的优化,而另一种模态不受影响,能够摆脱有限的优化努力,获得足够的训练。采用带有OGM策略的SGD优化方法,分别控制了各模态的优化过程,缓解了不平衡问题。
Generalization enhancement
在SGD优化方法中,根据中心极限定理,当批大小m足够大时,式7中的梯度
g
˜(
θ
t
u
)
g˜(θ_t^ u)
g˜(θtu)服从高斯分布,即
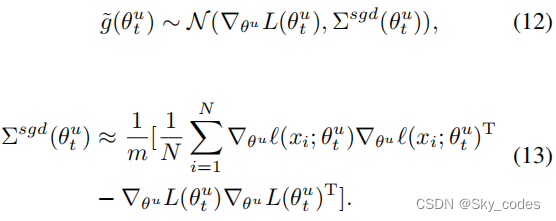
则方程7可以改写为,其中 ξ t ξ_t ξt为噪声项:
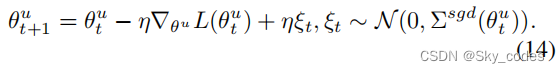
定理1 (SGD泛化能力)。SGD中的噪声与其泛化能力密切相关,较大的SGD噪声往往导致更好的泛化。SGD噪声的协方差与学习率与批处理大小的比值成正比。
根据定理1,梯度协方差(方程14中的 ξ t ξ_t ξt)值越高,往往会带来更好的泛化能力。当我们使用系数 k t u k_t^ u ktu来调节梯度时, θ u θ^u θu被更新为:
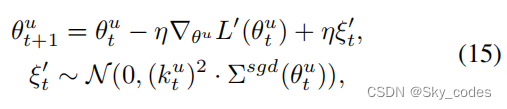
其中, η ∇ θ u L ′ ( θ t u ) = k t u ⋅ η ∇ θ u L ( θ t u ) η∇_{θ^u} L'(θ_t ^u)= k_t^ u·η∇_{θ^u} L(θ_t^ u) η∇θuL′(θtu)=ktu⋅η∇θuL(θtu)。根据方程10, k t u k_t^ u ktu∈(0,1]。当然,当学习率和批量大小固定时, ξ ′ t ξ't ξ′t的协方差小于原始 ξ t ξ_t ξt。降低SGD优化方法的泛化能力。因此,需要开发一种控制SGD噪声的方法,恢复泛化能力。
为了增强SGD噪声,我们引入了一种简单但有效的推广增强(GE)方法,该方法将一个随机采样的高斯噪声 h ( θ t u ) ∼ N ( 0 , Σ s g d ( θ t u )) h(θ_t^ u)∼N(0,Σ^{sgd}(θ_t^ u)) h(θtu)∼N(0,Σsgd(θtu))添加到梯度中,它具有与 g ˜( θ t u ) g˜(θ_t^ u) g˜(θtu)相同的协方差,并根据当前的迭代动态变化。然后,结合OGM方法,将 θ t u θ_t^ u θtu更新为:
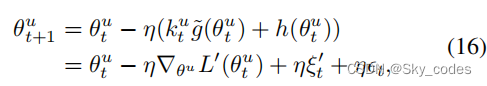
其中, ϵ t ∼ N ( 0 , Σ s g d ( θ t u )) ϵ_t∼N(0,Σ^{sgd}(θ_t^ u)) ϵt∼N(0,Σsgd(θtu))。由于 ϵ t ϵ_t ϵt和 ξ t ξ_t ξt是独立的,所以方程16可以重写为:
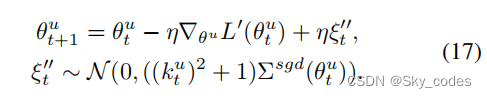
因此,SGD噪声的协方差被恢复,甚至增强。我们在算法1中提供了总体的OGM-GE策略,管道如图2所示。结合我们的策略,多模态模型的优化可以更加平衡,保证对各模态的泛化能力。

实验
作者实验部分表格分散,大家有需要可以去看论文。
消融
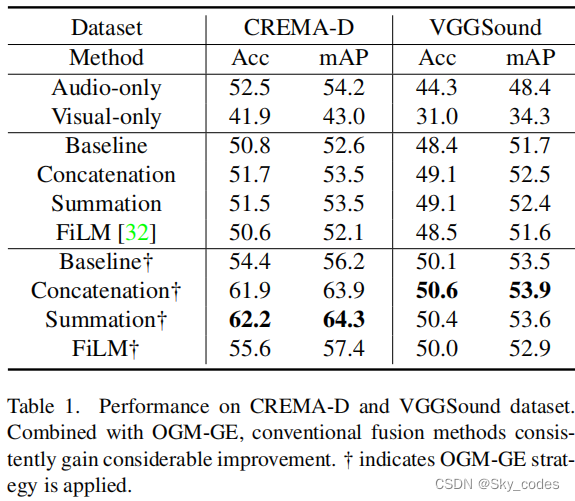
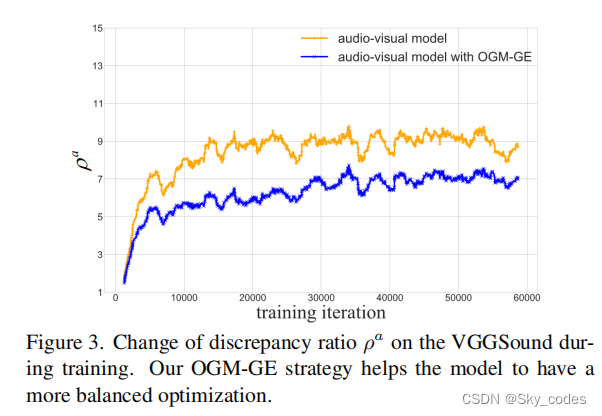
为了进一步分析OGM-GE,我们监测了训练过程中差异比的变化。如图1所示,经过调制后,多模态模型下的视听模态的性能都得到了改善。一个有趣的观察结果是,我们的方法一开始的表现不如其他方法,但最终的表现优于其他方法。这是因为我们以更好的性能调制梯度,减轻模态的优化,通过此我们的方法可以进一步利用其他模态的信息,最终获得改进。此外,从图3中可以看出,应用OGM-GE后,差异比ρa明显降低,这是我们的方法有效性的具体证据。然而,需要注意的是,这两种模式对学习目标的贡献通常不相同,因为在各种管理数据集中存在自然不平衡,因此这两种模式对学习目标的自然不平衡。表1和图1中的结果也可以说明这一点。
还有其他消融,具体看论文。
总结
在本文中,我们提出了一种简单而有效的多模态学习策略,即基于广义增强的动态梯度调制(OGM-GE),以缓解优化不平衡问题,促进这两种模式的利用。该方法在不同的设置下,在四个具有代表性的多模态数据集上获得了一致的性能增益,通常可以作为普通融合方法和专门设计的融合方法以及现有多模态模型的灵活插件策略。
-
限制。然而,仍然存在一个未解决的问题,即使配备了OGM-GE,在多模态模型中的单模态性能仍然不能超过最佳的单模态模型。我们假设,仅仅利用面向优化的方法并不能彻底解决不平衡问题,因此必须研究不同的方法,如更先进的融合策略或网络架构。我们把这个有趣的挑战留给了未来的工作。此外,OGM-GE的多功能性表明,它在更多模态场景中具有巨大的潜力,可能包括深度、光流、语言等。
-
更广泛的影响。所提出的方法是在可能包含偏差的管理数据集上进行训练的,导致模型不可避免地学习到这些信息。这个问题值得进一步考虑。