剑指 Offer 55 - II. 平衡二叉树
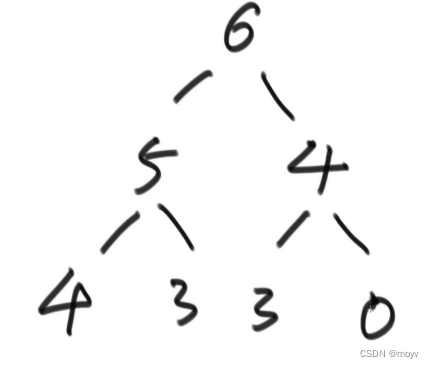
输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

来自力扣K神的解法1，真的是太巧妙了！
方法recur检查以node为根节点的树是不是平衡的；
使用-1标记“这个树不平衡”，而如果树是平衡的，那么可以直接返回树的高度。如此一来，recur的返回值类型就可以统一为int。

class Solution {
    public boolean isBalanced(TreeNode root) {
        return recur(root)!=-1;
    }
    public int recur(TreeNode node){
        if(node==null) return 0;

        int leftLen = recur(node.left);
        if(leftLen==-1) return -1;// 如果判断到左树是不平衡的，那么直接返回不平衡

        int rightLen = recur(node.right);
        if(rightLen==-1) return -1;

        return Math.abs(rightLen-leftLen)<=1?Math.max(leftLen,rightLen)+1:-1;
        
    }
}

来自力扣K神的解法2，一种比较自然的思路，首先算左树右树的深度，判断当前树是否满足“左子树深度与右子树深度相差不得超过1”的条件，然后判断左树右树是否是平衡树，对这三个boolean取&&，得到的结果即当前树是不是平衡树。

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;
        return Math.abs(depth(root.left)-depth(root.right))<=1&&isBalanced(root.right)&&isBalanced(root.left);

    }
    public int depth(TreeNode node){
        if(node==null) return 0;
        return Math.max(depth(node.left),depth(node.right))+1;
    }
}

下面的解法参考了左程云算法课上所介绍的关于二叉树题目的套路

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root==null) return true;

        return func(root).isBal;

    }

    class info{// 左右孩子节点需要向父节点反馈info信息
        int leftLen;// 当前左树高度
        int rightLen;// 当前右树高度
        boolean isBal;// 当前结点为根节点的子树是否是平衡的

        public info(int l, int r, boolean isb){
            leftLen=l;
            rightLen=r;
            isBal=isb;
        }
    }

    public info func(TreeNode node){
        if(node==null){
            return new info(0,0,true);
        }

        info leftInfo = func(node.left);
        info rightInfo = func(node.right);
        
        int leftLen = Math.max(leftInfo.leftLen,leftInfo.rightLen)+1;
        int rightLen=Math.max(rightInfo.leftLen,rightInfo.rightLen)+1;
        boolean isBal = leftInfo.isBal&&rightInfo.isBal;
        if(isBal){
            isBal = Math.abs(leftLen-rightLen)<=1;
        }
        return new info(leftLen,rightLen,isBal);
    }

}