堆
满二叉树可以用一个数组中从0开始的连续一段来记录
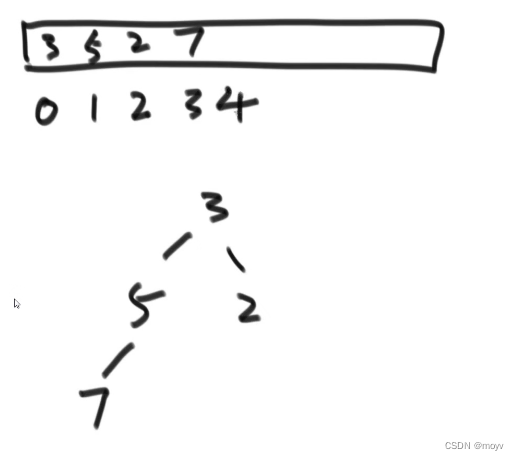
i i i位置左孩子: 2 ∗ i + 1 2*i+1 2∗i+1,右孩子: 2 ∗ i + 2 2*i+2 2∗i+2,父: ( i − 1 ) / 2 (i-1)/2 (i−1)/2
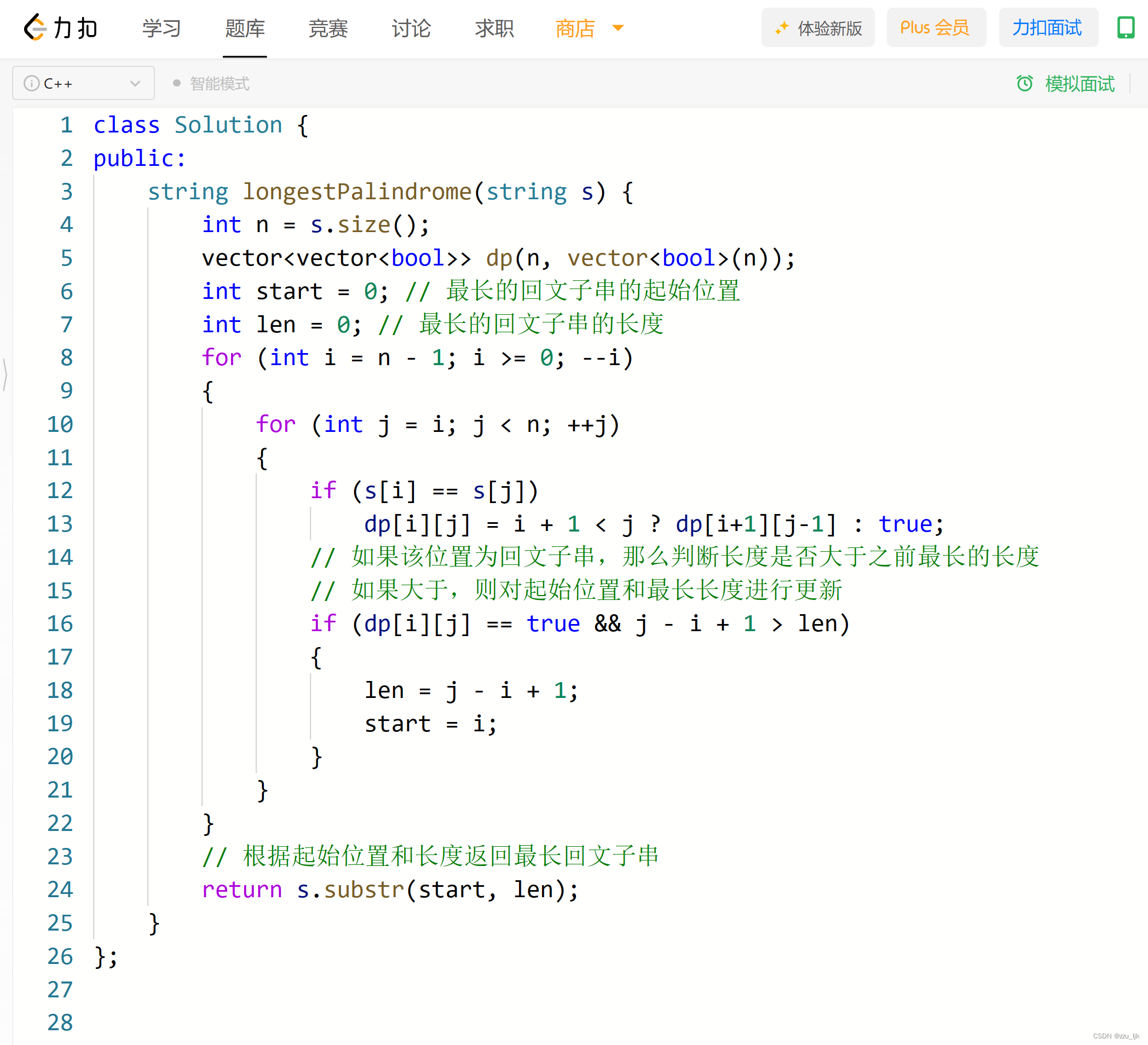
大根堆
每一棵子树的根为最大值
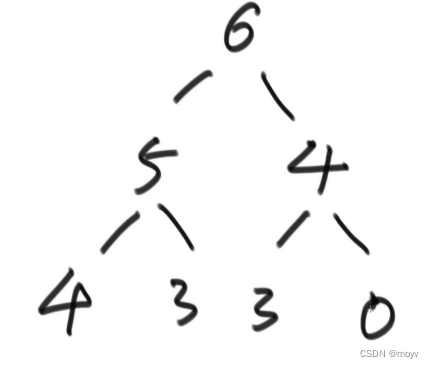
小根堆
每一棵子树的根为最小值
建大根堆
不断地根据公式(父: ( i − 1 ) / 2 (i-1)/2 (i−1)/2)找到父,如果比父大,就交换,什么时候到整棵树的根或者不再比父大,停止。
public static void heapInsert(int[] arr, int index) {
while (arr[index] > arr[(index - 1) / 2]) {
swap(arr, index, (index - 1) /2);
index = (index - 1)/2 ;
}
}
注意: ( 0 − 1 ) / 2 = 0 (0-1)/2=0 (0−1)/2=0
堆的删除操作
要求删除输入的数中最大的数(也就是根),然后剩余的数还要是一个堆。
heapify:把堆中的最后一个数放到根,然后 h e a p s i z e − − heapsize-- heapsize−−,此时整体可能不是堆。然后用此时的根和 x _ c h i l d = m a x ( 左孩子、右孩子 ) x\_child=max(左孩子、右孩子) x_child=max(左孩子、右孩子)比较,如果根 < x _ c h i l d <x\_child <x_child






![[C++项目] Boost文档 站内搜索引擎(1): 项目背景介绍、相关技术栈、相关概念介绍...](https://img-blog.csdnimg.cn/img_convert/a0d24a580831ed4856a2c7d8331b55e8.png)