MPDIoU: A Loss for Efficient and Accurate Bounding BoxRegression--论文学习笔记

news2024/9/23 13:21:19

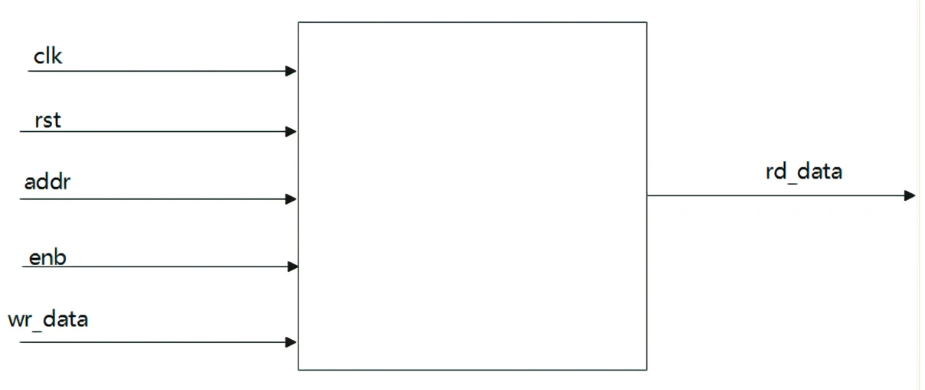
超越GIoU/DIoU/CIoU/EIoU MPDIoU让YOLOv7和YOLACT双双涨点

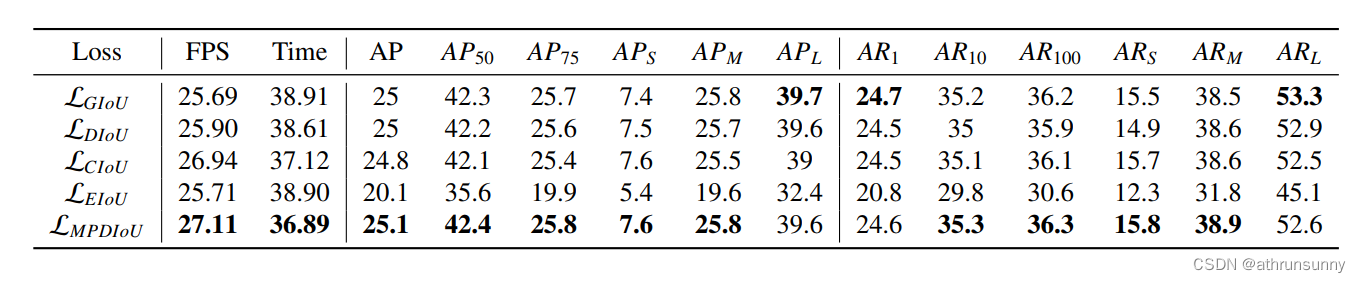
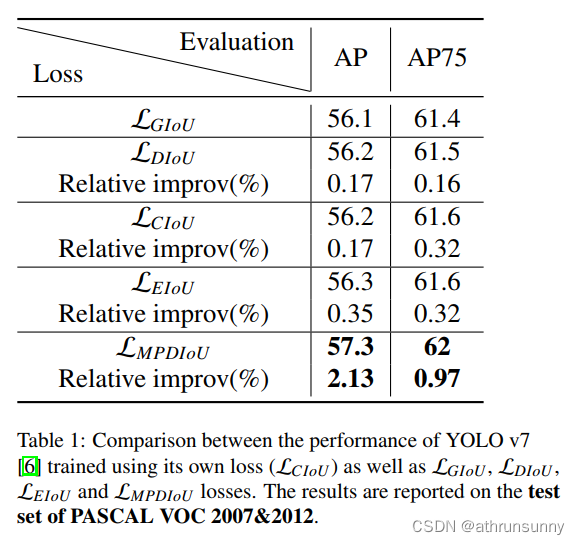
目标检测上的指标对比：

论文地址： [2307.07662] MPDIoU: A Loss for Efficient and Accurate Bounding Box Regression (arxiv.org)

摘要

边界框回归（Bounding Box Regression，BBR）在目标检测和实例分割中被广泛应用，是定位目标的重要步骤。然而，大多数现有的边界框回归损失函数在预测框与实际标注框具有相同的宽高比但宽度和高度值完全不同的情况下无法进行优化。为了解决上述问题，作者充分探索了水平矩形的几何特征，提出了一种基于最小点距离的边界框相似度比较度量——MPDIoU，其中包含了现有损失函数中考虑的所有相关因素，例如重叠或非重叠面积、中心点距离以及宽度和高度的偏差，同时简化了计算过程。在此基础上，作者提出了一种基于MPDIoU的边界框回归损失函数，称为 $L_{MPDIoU}$ 。实验结果表明，将MPDIoU损失函数应用于最先进的实例分割（如YOLACT）和目标检测（如YOLOv7）模型，在PASCAL VOC、MS COCO和IIIT5k数据集上优于现有的损失函数。

Introduction

目标检测和实例分割是计算机视觉中两个重要的问题，在过去几年中吸引了大量研究人员的兴趣。大多数最先进的目标检测器（例如YOLO系列，Mask R-CNN，Dynamic R-CNN和DETR）依赖于边界框回归（BBR）模块来确定目标的位置。基于这种模式，设计良好的损失函数对于BBR的成功非常重要。到目前为止，大多数现有的BBR损失函数可分为两类：1、基于 $l_{n}$ 数的损失函数；2、基于交并比（IoU）的损失函数。

然而，现有的大多数BBR损失函数在不同预测结果下具有相同的值，这降低了边界框回归的收敛速度和准确性。因此，考虑到现有BBR损失函数的优缺点，并受到水平矩形的几何特征启发，作者尝试设计一种基于最小点距离的新型损失函数 $L_{MPDIoU}$ ，用MPDIoU作为新的度量标准，比较边界框回归过程中预测边界框与实际标注边界框之间的相似性。作者还提供了一个简单易实现的解决方案，用于计算两个轴对齐矩形之间的MPDIoU，使其可以作为评估指标纳入最先进的目标检测和实例分割算法中，并在一些主流的目标检测、场景文本识别和实例分割数据集（如PASCAL VOC，MS COCO，IIIT5k和MTHv2）上进行测试，以验证作者提出的MPDIoU的性能。

本文的贡献总结如下：

作者考虑了现有IoU-based损失和 $l_{n}$ -norm损失的优缺点，并提出了一种基于最小点距离的IoU损失，即 $L_{MPDIoU}$ ，来解决现有损失函数的问题，并获得更快的收敛速度和更准确的回归结果。
作者在目标检测、字符级场景文本识别和实例分割任务上进行了广泛的实验。出色的实验结果验证了提出的MPDIoU损失的优越性。详细的消融研究展示了不同损失函数和参数值设置的效果。

相关工作就是介绍了之前的几种IoU（GIoU/DIoU/CIoU/EIoU），这里就跳过了，感兴趣的话可以看这里：IoU Loss综述，对几种IoU做了总结

Intersection over Union with Minimum Points Distance

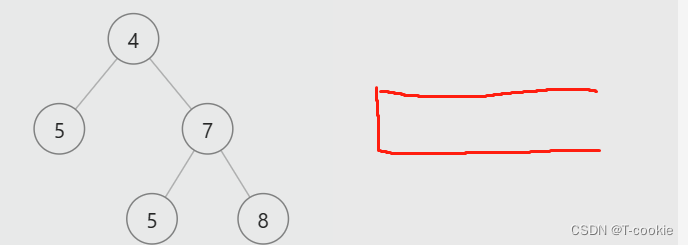
在分析了IoU系列损失函数的优势和劣势之后，开始思考如何提高边界框回归的准确性和效率。通常情况下，使用左上角和右下角点的坐标来定义一个唯一的矩形。受到边界框几何特性的启发，作者设计了一种新颖的基于交并比的度量标准，名为MPDIoU，直接最小化预测边界框与实际标注边界框之间的左上角和右下角点距离。

MPDIoU的计算过程总结在算法1中：

通过使用MPDIoU作为新的损失度量，作者期望能够改善边界框回归的训练效果，提高收敛速度和回归精度。

总结一下，提出的MPDIoU简化了两个边界框之间的相似性比较，适用于重叠或非重叠的边界框回归。因此，在2D/3D计算机视觉任务中，MPDIoU可以很好地替代交并比作为所有性能指标的度量。在本文中，作者仅关注2D目标检测和实例分割，可以将MPDIoU轻松应用为度量和损失函数。

MPDIoU as Loss for Bounding Box Regression

在训练阶段，通过最小化以下损失函数，使得模型预测的每个边界框Bprd = [xprd, yprd, wprd, hprd]T趋近于其对应的真实标注边界框Bgt = [xgt, ygt, wgt, hgt]T：

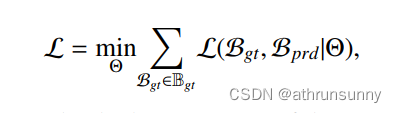
其中Bgt表示真实标注边界框的集合， $\Theta$ 表示用于回归的深度模型的参数。典型的损失函数L采用 $l_{n}$ 范数，例如均方误差（MSE）损失和 $Smooth-{l_{1}}$ 损失，这些损失函数在目标检测、行人检测、场景文本识别、3D目标检测、姿态估计和实例分割等任务中得到广泛应用。然而，最近的研究表明，基于 $l_{n}$ 范数的损失函数与评估指标——交并比（IoU）并不一致，因此提出了基于IoU的损失函数。基于前面一节中MPDIoU的定义，作者定义基于MPDIoU的损失函数如下：

因此，现有边界框回归损失函数的所有因素都可以通过4个点的坐标来确定。转换公式如下所示：

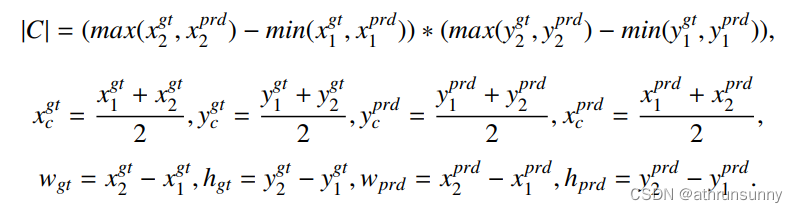
在上述公式中， $\left | C \right |$ 表示覆盖Bgt和Bprd的最小外接矩形的面积， $\left (x_{c}^{gt},y_{c}^{gt} \right )$ 和 $\left (x_{c}^{prd},y_{c}^{prd} \right )$ 分别表示真实标注边界框和预测边界框的中心点坐标。 ${w_{gt}}$ 和 ${h_{gt}}$ 表示真实标注边界框的宽度和高度， ${w_{prd}}$ 和 ${h_{prd}}$ 表示预测边界框的宽度和高度。

从公式（10）-（12）中可以发现所有现有损失函数中考虑的因素都可以通过左上角点和右下角点的坐标来确定，例如非重叠面积、中心点距离、宽度和高度的偏差，这意味着作者提出的 $L_{MPDIoU}$ 不仅考虑全面，还简化了计算过程。

根据定理3.1，如果预测边界框和真实标注边界框具有相同的宽高比，那么预测边界框位于真实标注边界框内的 $L_{MPDIoU}$ 值低于预测边界框位于真实标注边界框外的情况。这一特性保证了边界框回归的准确性，倾向于提供具有较少冗余的预测边界框。

考虑到真实标注边界框Bgt是一个面积大于零的矩形，即Agt > 0。算法2中的条件（1）和算法2中的条件（6）确保了预测面积Aprd和交集面积I为非负值，即Aprd ≥ 0 和 I ≥ 0，对于∀Bprd ∈ R4。

因此，对于任何预测边界框Bprd = (x1prd, y1prd, x2prd, y2prd) ∈ R4，其并集面积U > 0。这确保了交并比的分母在任何预测输出值下都不会为零。此外，对于任何Bprd = (x1prd, y1prd, x2prd, y2prd) ∈ R4的值，其并集面积总是大于等于交集面积，即U ≥ I。因此， $L_{MPDIoU}$ 始终有界，即0 ≤ $L_{MPDIoU}$ < 3，对于∀Bprd ∈ R4。

当IoU = 0时：对于MPDIoU损失，作者有 $L_{MPDIoU} = 1 - MPDIoU = 1 + \frac{d_{1}^{2}}{d^{2}} + \frac{d_{2}^{2}}{d^{2}} -IoU$ 。在Bgt和Bprd不重叠的情况下，即IoU=0，MPDIoU损失可以简化为 $L_{MPDIoU} = 1 - MPDIoU = 1 + \frac{d_{1}^{2}}{d^{2}} + \frac{d_{2}^{2}}{d^{2}}$ 。在这种情况下，通过最小化 $L_{MPDIoU}$ ，作者实际上是在最小化 $\frac{d_{1}^{2}}{d^{2}} + \frac{d_{2}^{2}}{d^{2}}$ 。这一项是一个介于0和1之间的归一化度量，即 $0\leq \frac{d_{1}^{2}}{d^{2}} + \frac{d_{2}^{2}}{d^{2}} < 2$ 。