## 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 退火算法原理
1.1 物理背景
在热力学上,退火(annealing)现象指物体逐渐降温的物理现象,温度愈低,物体的能量状态会低;够低后,液体开始冷凝与结晶,在结晶状态时,系统的能量状态最低。大自然在缓慢降温(亦即,退火)时,可“找到”最低能量状态:结晶。但是,如果过程过急过快,快速降温(亦称「淬炼」,quenching)时,会导致不是最低能态的非晶形。
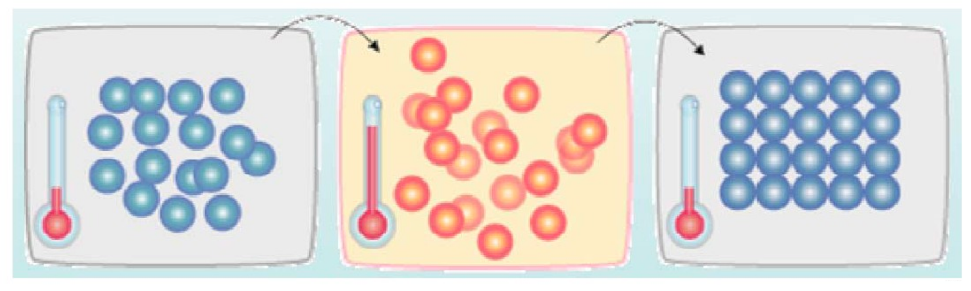
如下图所示,首先(左图)物体处于非晶体状态。我们将固体加温至充分高(中图),再让其徐徐冷却,也就退火(右图)。加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小(此时物体以晶体形态呈现)。
1.2 背后的数学模型
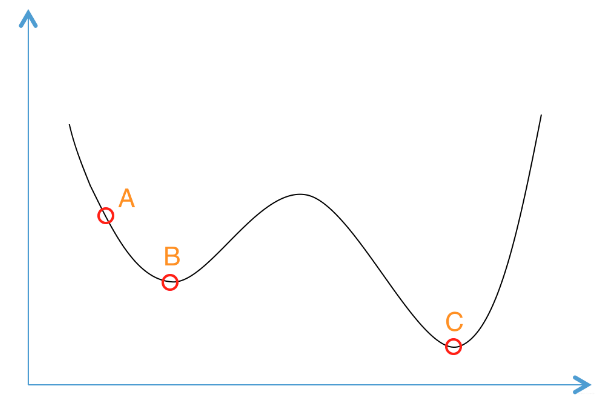
如果你对退火的物理意义还是晕晕的,没关系我们还有更为简单的理解方式。想象一下如果我们现在有下面这样一个函数,现在想求函数的(全局)最优解。如果采用Greedy策略,那么从A点开始试探,如果函数值继续减少,那么试探过程就会继续。而当到达点B时,显然我们的探求过程就结束了(因为无论朝哪个方向努力,结果只会越来越大)。最终我们只能找打一个局部最后解B。
根据Metropolis准则,粒子在温度T时趋于平衡的概率为exp(-ΔE/(kT)),其中E为温度T时的内能,ΔE为其改变数,k为Boltzmann常数。Metropolis准则常表示为
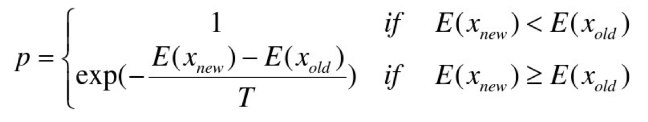
Metropolis准则表明,在温度为T时,出现能量差为dE的降温的概率为P(dE),表示为:P(dE) = exp( dE/(kT) )。其中k是一个常数,exp表示自然指数,且dE<0。所以P和T正相关。这条公式就表示:温度越高,出现一次能量差为dE的降温的概率就越大;温度越低,则出现降温的概率就越小。又由于dE总是小于0(因为退火的过程是温度逐渐下降的过程),因此dE/kT < 0 ,所以P(dE)的函数取值范围是(0,1) 。随着温度T的降低,P(dE)会逐渐降低。
我们将一次向较差解的移动看做一次温度跳变过程,我们以概率P(dE)来接受这样的移动。也就是说,在用固体退火模拟组合优化问题,将内能E模拟为目标函数值 f,温度T演化成控制参数 t,即得到解组合优化问题的模拟退火演算法:由初始解 i 和控制参数初值 t 开始,对当前解重复“产生新解→计算目标函数差→接受或丢弃”的迭代,并逐步衰减 t 值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。退火过程由冷却进度表(Cooling Schedule)控制,包括控制参数的初值 t 及其衰减因子Δt 、每个 t 值时的迭代次数L和停止条件S。
2 退火算法实现
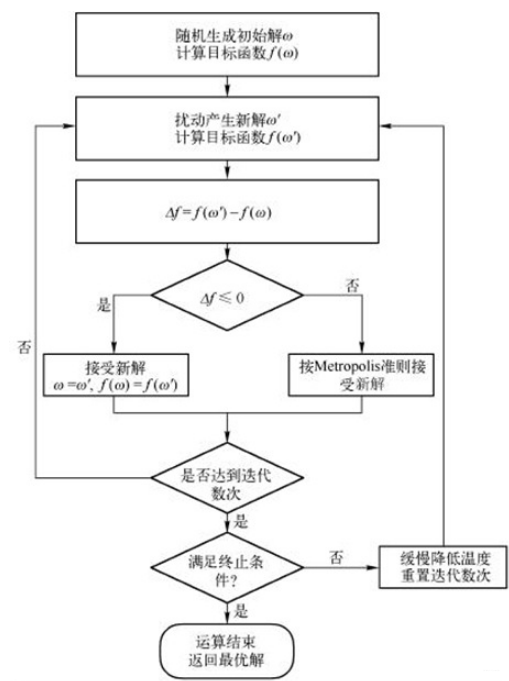
2.1 算法流程
(1) 初始化:初始温度T(充分大),初始解状态S(是算法迭代的起点), 每个T值的迭代次数L
(2) 对k=1,……,L做第(3)至第6步:
(3) 产生新解S′
(4) 计算增量Δt′=C(S′)-C(S),其中C(S)为评价函数
(5) 若Δt′<0则接受S′作为新的当前解,否则以概率exp(-Δt′/T)接受S′作为新的当前解.
(6) 如果满足终止条件则输出当前解作为最优解,结束程序。
终止条件通常取为连续若干个新解都没有被接受时终止算法。
(7) T逐渐减少,且T->0,然后转第2
2.2算法实现
import numpy as np
import matplotlib.pyplot as plt
import random
class SA(object):
def __init__(self, interval, tab='min', T_max=10000, T_min=1, iterMax=1000, rate=0.95):
self.interval = interval # 给定状态空间 - 即待求解空间
self.T_max = T_max # 初始退火温度 - 温度上限
self.T_min = T_min # 截止退火温度 - 温度下限
self.iterMax = iterMax # 定温内部迭代次数
self.rate = rate # 退火降温速度
#############################################################
self.x_seed = random.uniform(interval[0], interval[1]) # 解空间内的种子
self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值
#############################################################
self.solve() # 完成主体的求解过程
self.display() # 数据可视化展示
def solve(self):
temp = 'deal_' + self.tab # 采用反射方法提取对应的函数
if hasattr(self, temp):
deal = getattr(self, temp)
else:
exit('>>>tab标签传参有误:"min"|"max"<<<')
x1 = self.x_seed
T = self.T_max
while T >= self.T_min:
for i in range(self.iterMax):
f1 = self.func(x1)
delta_x = random.random() * 2 - 1
if x1 + delta_x >= self.interval[0] and x1 + delta_x <= self.interval[1]: # 将随机解束缚在给定状态空间内
x2 = x1 + delta_x
else:
x2 = x1 - delta_x
f2 = self.func(x2)
delta_f = f2 - f1
x1 = deal(x1, x2, delta_f, T)
T *= self.rate
self.x_solu = x1 # 提取最终退火解
def func(self, x): # 状态产生函数 - 即待求解函数
value = np.sin(x**2) * (x**2 - 5*x)
return value
def p_min(self, delta, T): # 计算最小值时,容忍解的状态迁移概率
probability = np.exp(-delta/T)
return probability
def p_max(self, delta, T):
probability = np.exp(delta/T) # 计算最大值时,容忍解的状态迁移概率
return probability
def deal_min(self, x1, x2, delta, T):
if delta < 0: # 更优解
return x2
else: # 容忍解
P = self.p_min(delta, T)
if P > random.random(): return x2
else: return x1
def deal_max(self, x1, x2, delta, T):
if delta > 0: # 更优解
return x2
else: # 容忍解
P = self.p_max(delta, T)
if P > random.random(): return x2
else: return x1
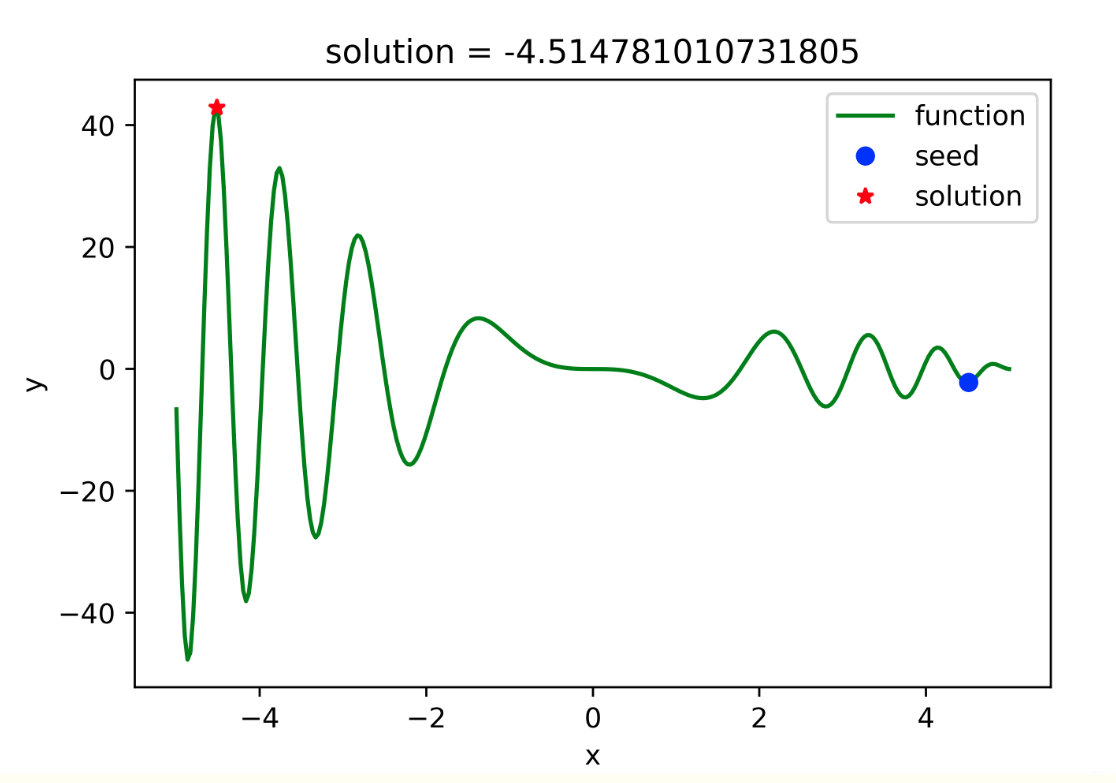
def display(self):
print('seed: {}\nsolution: {}'.format(self.x_seed, self.x_solu))
plt.figure(figsize=(6, 4))
x = np.linspace(self.interval[0], self.interval[1], 300)
y = self.func(x)
plt.plot(x, y, 'g-', label='function')
plt.plot(self.x_seed, self.func(self.x_seed), 'bo', label='seed')
plt.plot(self.x_solu, self.func(self.x_solu), 'r*', label='solution')
plt.title('solution = {}'.format(self.x_solu))
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.savefig('SA.png', dpi=500)
plt.show()
plt.close()
if __name__ == '__main__':
SA([-5, 5], 'max')
实现结果