目录
一,堆的概念
二, 堆的存储结构
三, 堆的实现
3.1 shiftDown()
3.2 shiftUp()
3.3 shiftDown 与 shiftUp 的时间复杂度
四,堆排序
一,堆的概念
堆常用于实现优先队列(Priority Queue)等应用,其中可以快速查找和删除具有最大(或最小)优先级的元素。堆的操作包括插入新元素、移除堆中的顶部元素(即最值),以及对现有堆进行调整以满足堆序属性。常见的堆调整操作是"上浮"(上滤)和"下沉"(下滤)。
堆具有以下两个主要特点:
- 堆是一个完全二叉树
- 堆中的每个节点的值都要大于等于(或小于等于)其子节点的值。
二, 堆的存储结构
从堆的概念可知,堆在逻辑结构上是一棵完全二叉树,因此可以层序的规则采用顺序的方式来高效存储,也就是说,堆是使用顺序表来存储的,画个图理解一下:
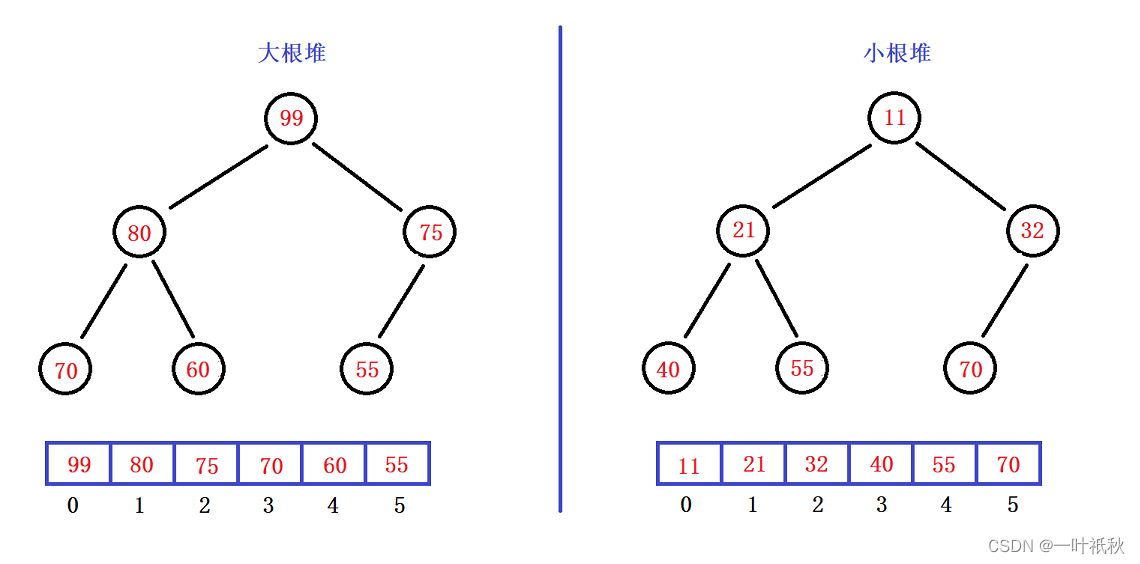
将元素存储到数组中后,可以根据完全二叉树的性质对树进行还原。假设i为节点在数组中的下标,则有:
- 如果i = 0,则 i 表示的节点为根节点,否则 i 节点的双亲节点为 (i - 1)/2
- 如果2 * i + 1 小于节点个数,则节点 i 的左孩子下标为2 * i + 1,否则没有左孩子
- 如果2 * i + 2 小于节点个数,则节点 i 的右孩子下标为2 * i + 2,否则没有右孩子
三, 堆的实现
在此实现的是大根堆:
public class Heap {
private int[] elem;
private int usedSize;
public Heap(int[] arr){
elem = new int[arr.length];
createHeap(arr);
}
//建堆
public void createHeap(int[] arr){
for (int i = 0; i < arr.length; i++) {
elem[i] = arr[i];
usedSize++;
}
for (int parent = (usedSize-2)/2; parent >= 0; parent--) {
shiftDown(parent,usedSize);
}
}
//向下调整
public void shiftDown(int parent, int len){}
public void swap(int i, int j){
int tmp = elem[i];
elem[i] = elem[j];
elem[j] = tmp;
}
//入堆
public void push(int val){}
public boolean isFull(){
return usedSize == elem.length;
}
//向上调整
public void shiftUp(int child){}
//出堆顶元素
public int poll(){
if(isEmpty()){
System.out.println("堆中没有元素");
return -1;
}
swap(0,usedSize-1);//将头尾交换
usedSize--;//去掉堆顶元素
shiftDown(0,usedSize);//重新排序
return elem[usedSize];//返回堆顶元素
}
public boolean isEmpty(){
return usedSize == 0;
}
//得到堆顶元素
public int peek(){
if(!isEmpty()){
return elem[0];
}
System.out.println("堆中没有元素");
return -1;
}
}
堆中最核心的代码就是 shiftDown() 和 shiftUp() 方法的实现,其他的方法看看就懂了,下面来详细讲一讲这两个方法的实现
3.1 shiftDown()
比如说我们要将{27,15,19,18,28,34,65,49,25,37}这个数组变成一个堆,我们要如何实现,思路:先找到最后一棵子树,将它变成堆后,依次遍历其他的子树,直到最后一棵子树的根节点是整棵树的根节点结束,看下图:

代码如下:
public void shiftDown(int parent, int len){
int child = 2*parent + 1;
while(child < len){
if(child+1 < len && elem[child] < elem[child+1]){
child++;
}
if(elem[parent] < elem[child]){
swap(parent,child);
parent = child;
child = 2*parent + 1;
}else{
break;
}
}
}3.2 shiftUp()
该方法是在插入一个元素时,将其以堆的形式插入,本质上shiftDown 与 shiftUp 的思路差不多:

public void shiftUp(int child){
int parent = (child-1)/2;
while(parent >= 0){
if(elem[child] > elem[parent]){
swap(child,parent);
child = parent;
parent = (child-1)/2;
}else {
break;
}
}
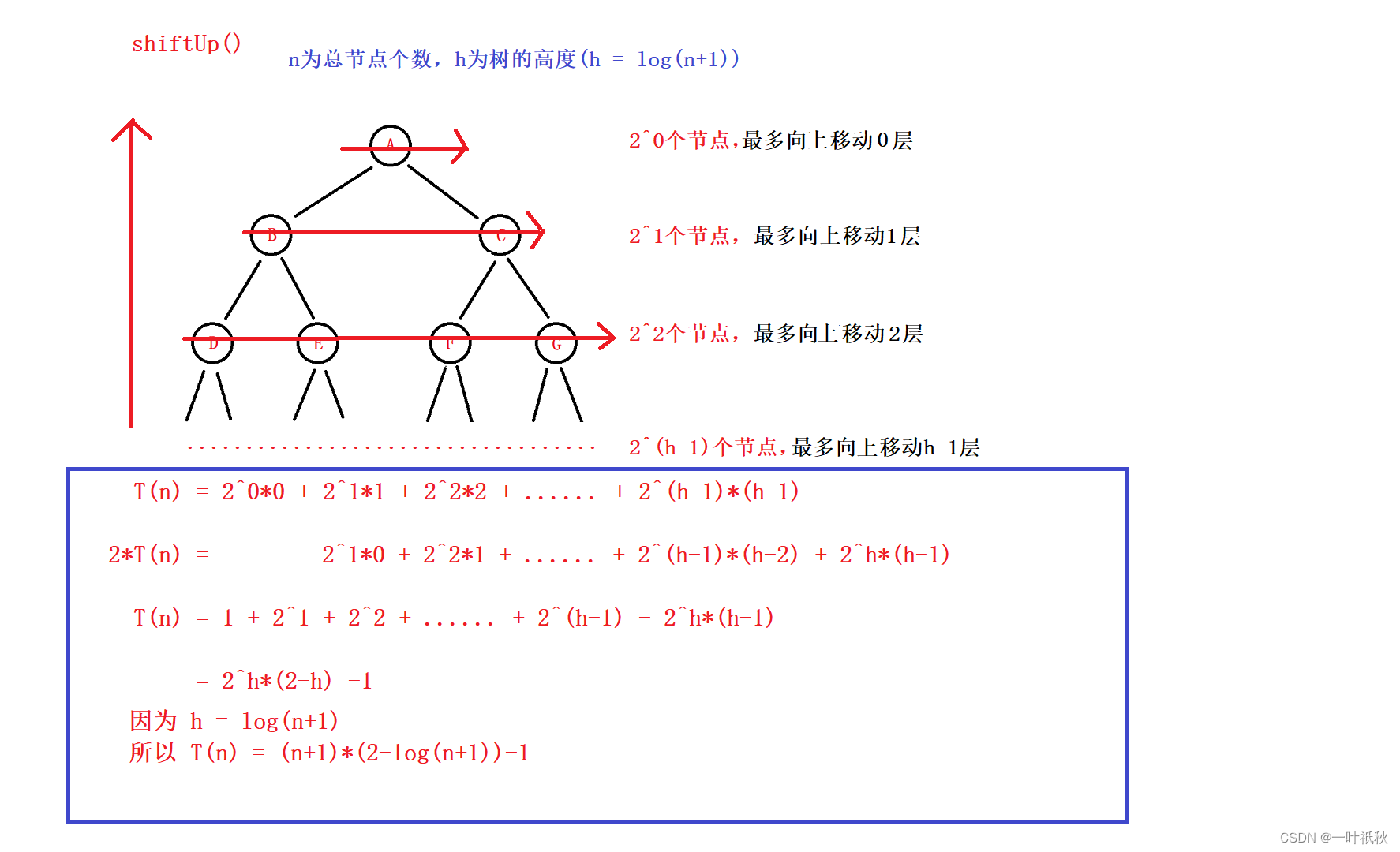
}3.3 shiftDown 与 shiftUp 的时间复杂度

四,堆排序
比如我们要进行升序排序,我们先要建立一个大根堆,再将根节点与最后一个节点交换,这个时候最后一个节点一定是的最大的,然后进行shiftDown,再将根节点与倒数第二个节点交换,依次类推。代码如下:
/**
* 堆排序
* 时间复杂度:O(N*logN)
* 空间复杂度:O(1)
* 不稳定
*/
public void heapSort(int[] arr){
createHeap(arr);
int end = arr.length-1;
while(end > 0){
swap(arr,0,end);
shiftDown(arr,0,end);
end--;
}
}
private void shiftDown(int[] arr, int parent,int len) {
int child = 2*parent+1;
while(child < len){
if(child+1 < len && arr[child] < arr[child+1]){
child++;
}
if(arr[child] > arr[parent]){
swap(arr,child,parent);
parent = child;
child = 2*parent+1;
}else{
break;
}
}
}
public void swap(int[] arr, int i, int j){
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public void createHeap(int[] array) {
for (int parent = (array.length-2)/2; parent >= 0; parent--) {
shiftDown(array,parent,array.length);
}
}