整数规划——第一章 引言

整数规划是带整数变量的最优化问题，即最大化或最小化一个全部或部分变量为整数的多元函数受约束于一组等式和不等式条件的最优化问题。许多经济、管理、交通、通信和工程中的最优化问题都可以用整数规划来建模。

考虑一个电视机工厂的生产计划问题，如果线性规划模型给出的最优生产计划是每天生产102。4台，则可以选择每天102或103台的生产计划。另一方面，若考虑的问题是仓库的选址问题，设线性规划给出的最优解是在甲地点建或买0。6个仓库，在乙地点建或买0。4个仓库，因仓库的个数必须是整数，这时线性规划的解不能提供任何有用的决策方案。实际上，除了可以描述决策变量的离散性外，整数变量可以帮助我们刻画最优化建模中的许多约束条件，如逻辑关系、固定费用、可选变量的上界、顺序和排序关系、分片线性函数等。

整数规划的历史可以追溯到20世纪50年代，运筹学创始人和线性规划单纯形算法发明者Dantzig首先发现可以用0-1变量来刻画最优化模型中的固定费用、变量上界、非凸分片线性函数等。他和Fulkerson及Johnson对旅行售货员问题(TSP)的研究成为后来的分枝割方法和现代混合整数规划算法的开端。1958年，Gomory发现了第一个一般线性整数规划的收敛算法——割平面方法。随着整数规划理论和算法的发展，整数规划已成为应用最广泛的最优化方法之一，特别是近年来整数规划算法技术和软件系统（如CPLEX)的发展和推广，整数规划在生产企业、服务、运营管理、交通、通信等领域得到了极大的应用和发展。

1.1 分类与建模

1.1.1 线性混合整数规划

线性混合整数规划（Mixed integer program/programming，MIP）的一般形式为：

$$\begin{array}{rl}(\text{MIP})& \min c^{T}x+h^{T}y,\\ & s.t.Ax+Gy\le b,x\in {\mathbb{Z}}_{+}^n,y\in {\mathbb{R}}_{+}^p,\end{array}$$

其中 ${\mathbb{Z}}_{+}^n$ 是 $n$ 维非负整数向量集合，${\mathbb{R}}_{+}^p$ 是$p$ 维非负实数向量集合。

如果问题（MIP）中没有连续决策变量，则（MIP）就是一个（纯）线性整数规划：

$$\begin{array}{rl}(\text{IP})& \min c^{T}x,\\ & s.t.Ax\le b,x\in {\mathbb{Z}}_{+}^n,\end{array}$$

背包问题 设有一个背包，其承重为 $b$ 。考虑n件物品，其中第 $j$ 件的重量为 ${\alpha }_j$ ，价值为$c_j$。问如何选取物品装入背包，使背包内物品的总价值最大？

设

$$x_j=\{\begin{array}{ll}1,& 若选取第j件物品，\\ 0,& 若不选取.\end{array}$$

则背包问题可以表示为下列线性0-1规划：

max ⁡ ∑ j = 1 n c j x j , s . t .   ∑ j = 1 n a j x j ≤ b , x ∈ { 0 , 1 } n . \begin{aligned}&\max \sum_{j=1}^n c_jx_j,\\ &s.t.\ \sum_{j=1}^n a_jx_j\le b,\\ &\quad\quad x\in \{0,1\}^n. \end{aligned} ​maxj=1∑n​cj​xj​,s.t. j=1∑n​aj​xj​≤b,x∈{0,1}n.​

指派问题 设有 $m$ 台机器，$n$ 个工件，第 $i$ 台机器的可用工时数为 $b_i$ ，第 $i$ 台机器完成第 $j$ 件工件需要的工时数为 $a_{ij}$ ，费用为 $c_{ij}$ 。问如何最优指派机器生产。

设

$$x_{ij}=\{\begin{array}{ll}1,& 若第i个机器加工第j件工件，\\ 0,& 其他.\end{array}$$

则指派问题可以表示为如下0-1规划问题：

min ⁡ ∑ i = 1 n ∑ j = 1 n c i j x i j , s . t .   ∑ j = 1 n a i j x i j ≤ b i ,   i = 1 , . . . , m , ∑ i = 1 m x i j = 1 , j = 1 , . . . , n , x ∈ { 0 , 1 } n . \begin{aligned}&\min \sum_{i=1}^n\sum_{j=1}^n c_{ij}x_{ij},\\ &s.t.\ \sum_{j=1}^n a_{ij}x_{ij}\le b_i,\ i = 1,...,m,\\ &\quad\quad\sum_{i = 1}^m x_{ij} =1,j=1,...,n, \\ &\quad\quad x\in \{0,1\}^n. \end{aligned} ​mini=1∑n​j=1∑n​cij​xij​,s.t. j=1∑n​aij​xij​≤bi​, i=1,...,m,i=1∑m​xij​=1,j=1,...,n,x∈{0,1}n.​

集合覆盖问题 设某地区划分为若干个区域，需要建立若干个应急服务中心（如消防站、急救中心等），每个中心的建立都需要一笔建站费用，设候选中心的位置已知，每个中心可以服务的区域预先知道，问如何选取中心使该应急服务能覆盖整个地区且使建站费用最小。

记 M = { 1 , ⋅ ⋅ ⋅ , m } M=\{1,···,m\} M={1,⋅⋅⋅,m} 为该地区中的区域， N = { 1 , ⋅ ⋅ ⋅ , n } N=\{1,···,n\} N={1,⋅⋅⋅,n} 是可选的中心，设 $S\le M$ 为中心 $j\in N$ 可以服务的区域集合，$c_j$ 是中心 $j$ 的建站费用，定义0-1关联矩阵 $A=(a_{ij})$ ，其中如果 $i\in S_j$，$a_{ij}=1$ ，否则 $a_{ij}=0$ 。

设

$$x_j=\{\begin{array}{ll}1,& 若选取中心j，\\ 0,& 其他.\end{array}$$

则问题可以表述为：

min ⁡ ∑ j = 1 n c j x j , s . t .   ∑ j = 1 n a i j x j ≥ 1 , i = 1 , . . . , m , x ∈ { 0 , 1 } n . \begin{aligned}&\min \sum_{j=1}^n c_jx_j,\\ &s.t.\ \sum_{j=1}^n a_{ij}x_j\ge 1,i=1,...,m,\\ &\quad\quad x\in \{0,1\}^n. \end{aligned} ​minj=1∑n​cj​xj​,s.t. j=1∑n​aij​xj​≥1,i=1,...,m,x∈{0,1}n.​

旅行售货员问题（TSP） 设有一个旅行售货员需要去n个城市推销他的产品，他必须而且只能访问每个城市一次，并最后返回出发城市.设每个城市直接到达另一个城市的距离已知（如不能直接到达，则可设其距离为+∞），他应该如何选择旅行路线使得总的旅行距离最短？

设城市 $i$ 到城市 $j$ 的距离为 $c_{ij}$，设

$$x_{ij}=\{\begin{array}{ll}1,& 若他的旅游路线包括了直接从城市i到城市j的行程，\\ 0,& 其他.\end{array}$$

约束条件：

• 离开城市 $i$ 一次：

  $$\sum _{j\ne i}{x}_{ij}=1,i=1,...,n$$

• 到达城市 $j$ 一次：

  $$\sum _{i\ne j}{x}_{ij}=1,j=1,...,n$$

• 上面的约束条件使得每个城市正好经过一次，但仍可能包括含圈但不联通的路
  线，我们需要用下面的约束条件来去除这种情况发生：

  ∑ i ∈ S ∑ j ∉ S x i j ≥ 1 , ∀ S ⊂ N = { 1 , . . . , n } , S ≠ ∅ \sum_{i\in S}\sum_{j\not\in S}x_{ij}\ge 1,\quad \forall S\sub N=\{1,...,n\},S\not =\emptyset i∈S∑​j∈S∑​xij​≥1,∀S⊂N={1,...,n},S=∅

  或者

  $$\sum _{i\in S}\sum _{j\in S}{x}_{ij}\le |S|-1,\forall S\subset N,2\le |S|\le n-1$$

从而旅行售货员问题可以表示为：

min ⁡ ∑ i = 1 n ∑ j = 1 n c i j x i j , s . t .   ∑ j ≠ i x i j = 1 ,   i = 1 , . . . , n , ∑ i ≠ j m x i j = 1 , j = 1 , . . . , n , ∑ i ∈ S ∑ j ∈ S x i j ≤ ∣ S ∣ − 1 , ∀ S ⊂ N , 2 ≤ ∣ S ∣ ≤ n − 1 , x ∈ { 0 , 1 } n . \begin{aligned}&\min \sum_{i=1}^n\sum_{j=1}^n c_{ij}x_{ij},\\ &s.t.\ \sum_{j\not=i} x_{ij}=1,\ i = 1,...,n,\\ &\quad\quad\sum_{i \not= j}^m x_{ij} =1,j=1,...,n, \\ &\quad\quad\sum_{i\in S}\sum_{j\in S} x_{ij}\le |S|-1,\quad \forall S\sub N,\quad 2\le|S|\le n-1,\\ &\quad\quad x\in \{0,1\}^n. \end{aligned} ​mini=1∑n​j=1∑n​cij​xij​,s.t. j=i∑​xij​=1, i=1,...,n,i=j∑m​xij​=1,j=1,...,n,i∈S∑​j∈S∑​xij​≤∣S∣−1,∀S⊂N,2≤∣S∣≤n−1,x∈{0,1}n.​

1.1.2 非线性整数规划

一般非线性混合整数规划(Mixed-Integer Nonlinear Programming)问题可表示为;

$$\begin{array}{rl}(\text{MINLP})& \min f(x,y),\\ & s.t.g_i(x,y)\le b_i,i=1,...,m,\\ & x\in X,y\in Y\end{array}$$

此处的$f,g_i,i=1,...,m$ 是 ${\mathbb{R}}^{n+q}$ 上的实值函数，$X$ 是 ${\mathbb{Z}}^n$ 的子集，$Y$ 是 ${\mathbb{R}}^q$ 的子集。

当（MINLP）中没有连续变量 $y$ 时，（MINLP）即是一个（纯）非线性整数规划：

$$\begin{array}{rl}(\text{NLIP})& \min f(x,y),\\ & s.t.g_i(x,y)\le b_i,i=1,...,m,\\ & x\in X,y\in Y\end{array}$$

最大割问题 设 $G=(V,E)$ 是有 $n$ 个顶点的无向图，设边 $(i,j)$ 上的权为 $w_{ij}(w_{ij}=w_{ji}\ge 0)$。图 $G$ 的一个割 $(S,S^{\prime })$ 是指 $n$ 个顶点上的一个分割：$S\cap S^{\prime }=\varnothing ,S\cup S^{\prime }=V$。最大割问题是求一个分割 $(S,S^{\prime })$ 使连接 $S$ 和 $S^{\prime }$ 之间的所有边上的权最大。

设 $x_i = 1\ \text{if} \ \ i\in S,\ x_i = -1 \ \text{if} \ \ i\in S’ $，则分割 $(S,S^{\prime })$ 上的权为：

$$\frac{1}{2}(\frac{1}{2}\sum _{i,j=1}^n{w}_{ij}-\frac{1}{2}\sum _{i,j=1}^n{w}_{ij}{x}_i{x}_j)=\frac{1}{4}\sum _{i,j=1}^n{w}_{ij}(1-x_i{x}_j).$$
所以最大割问题可以表示为：
max ⁡   1 4 ∑ i , j = 1 n w i j ( 1 − x i x j ) , s . t .   x ∈ { − 1 , 1 } n . \begin{aligned} &\max\ \frac{1}{4}\sum_{i,j=1}^n w_{ij}(1-x_ix_j),\\ & s.t.\ x\in \{-1,1\}^n. \end{aligned} ​max 41​i,j=1∑n​wij​(1−xi​xj​),s.t. x∈{−1,1}n.​
最大割问题是组合优化中著名的NP难问题，l995年，Goemans和Williamson对
最大割问题的SDP松弛给出了一个漂亮的结果：
$$f_{opt}\le f_{SDP}\le \alpha f_{opt},\alpha =1.138\cdot \cdot \cdot ,$$
这里 $f_{opt}$ 是最大割问题的最优值，$f_{SDP}$是SDP松弛问题的最优值

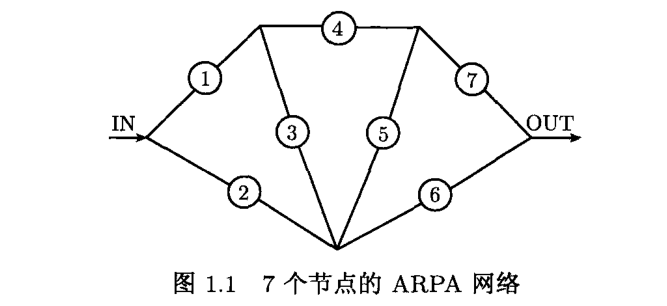
可靠性网络 考虑有 $n$ 个子系统的网络.设 $r_i(0<r_i<1)$ 是第 $i$ 个子系统中的部件可靠性，$x_i$ 表示第 $i$ 个子系统的冗余部件的个数。网络可靠性优化问题是求最优的冗余向量 $x=(x_1,\cdot \cdot \cdot ,x_n{)}^T$ 使网络的整体可靠性最大。

第 $i$ 个子系统的可靠性为
$$R_i(x_i)=1-(1-r_i{)}^{x_i},i=1,...,n$$
整个网络的可靠性 $R_s(x)$ 是关于 $R_1(x_1),...,R_n(x_n)$ 的增函数，下图所示的网络的可靠性为

$$R_s=R_6{R}_7+R_1{R}_2{R}_3(Q_6+R_6{Q}_7)+R_1{R}_4{R}_7{Q}_6(Q_2+R_2{Q}_3)$$
其中 $Q_i=1-R_i，i=1,...,n$，对应的最优冗余问题为：

max ⁡   R s ( x ) = f ( R 1 ( x 1 ) , . . . , R n ( x n ) ) , s . t .   g i ( x ) = ∑ j = 1 n g i j ( x j ) ≤ b i , i = 1 , . . . , m , x ∈ X = { x ∈ Z n ∣ 1 ≤ l j ≤ x j ≤ u j , j = 1 , . . . , n } \begin{aligned} &\max\ R_s(x)=f(R_1(x_1),...,R_n(x_n)),\\ & s.t.\ g_i(x)=\sum_{j=1}^ng_{ij}(x_j)\le b_i,\quad i=1,...,m,\\ &\quad\quad x\in X=\{x\in \Z^n|1\le l_j\le x_j\le u_j,j=1,...,n\} \end{aligned} ​max Rs​(x)=f(R1​(x1​),...,Rn​(xn​)),s.t. gi​(x)=j=1∑n​gij​(xj​)≤bi​,i=1,...,m,x∈X={x∈Zn∣1≤lj​≤xj​≤uj​,j=1,...,n}​
其中 $g_i(x),i=1,...,m$ 代表不同的资源消耗函数，例如费用、体积、重量等。

1.2 问题的挑战性

很多整数规划问题往往看上去很简单，数学模型也不复杂，如0-1背包问题、最大割问题等，但求解这类问题其实非常困难.绝大部分整数规划问题的可行域都只有有限多个可行点（决策方案），一个简单幼稚的想法是枚举所有的可行点，但是这样会使求解难度指数增加。大部分整数规划问题的困难在于：我们本质上只能使用枚举法或隐枚举法的思想来求解问题最优解，故当问题的规模越来越大时，算法的计算时间急剧增加。与此形成对照的是连续优化问题，我们知道，最简单的连续优化问题的可行点的个数也是无穷多个，但寻找可行域中的最优点并不需要借助枚举法的思想，因为利用微积分的工具可以刻画出最优点需要满足的一组容易验证的最优性条件，如KKT条件。故只有当算法需要枚举或部分枚举这些可行点时，可行域中可行点的个数才和问题的难度有关。

另外一个朴素的想法是“四舍五入”：求解相应的连续优化问题（丢掉整数约束)，然后对求得的解进行四舍五入，得到一个整数解.这个方法有两个问题：(1)一般很难通过四舍五入得到一个满足约束条件的可行解；(2)即使能求得一个可行解，其质量往往很差，即可能离最优解的距离很远，甚至和随机产生的可行解差不多。贪心算法往往可以帮助我们求到一个问题的近似解。例如，在0-1背包问题中，可以先进行排序：
$$\frac{c_{j1}}{a_{j1}}\ge \frac{c_{j2}}{a_{j2}}\ge ...\ge \frac{c_{jn}}{a_{jn}}$$
然后按照从大到小的顺序 $j_1,...,j_n$ 选取物品知道背包的容量 $b$ 不能再装下一个物品。

在实际应用中提出的很多整数规划问题的规模一般都很大，直接利用现有的算法和软件求解往往是不可能的.这就促使人们研究有效快速的近似算法或启发式算法以寻找问题的一个近似最优解或较好的可行解，如近年来发展起来的基于半定规划的随机化算法和各种针对具体整数规划和组合优化问题的近似算法。

参考资料

1. 整数规划 孙小玲，李瑞 北京，科学出版社 2010
2. Wolsey L A. Integer programming[M]. John Wiley & Sons, 2020.