文章目录

单个序列问题
- 示例1：最长递增子序列（不连续）
- - 思路
  - - DP数组含义
    - 递推公式
    - 初始化
    - 遍历顺序
  - 完整版
  - - 注意返回值问题
- 区分示例1：最长递增子数组
- - 区别：递推公式
- 示例2：最长连续递增序列（连续）
- - 完整版
- 示例3：最大子数组和（连续）
- - 思路
  - - DP数组含义
    - 递推公式
    - 初始化
  - 完整版
两个序列之间的问题
- 两个序列问题的DP数组定义
- - 初始化操作
- 示例1：最长重复子数组（连续）
- - 思路
  - - DP数组含义
    - 递推公式
    - 初始化
    - 遍历顺序
  - 完整版
- 示例2：最长公共子序列（不连续）
- - 思路
  - - DP数组含义
    - 递推公式（区分上题）
    - 初始化
  - 完整版
- 注意：递推dp[i-1]进一步理解
- 示例3：判断子序列
- - 思路
  - - DP数组含义
  - 完整版
  - 双指针做法：
  - 进阶做法：
- 示例4：不同的子序列
- - 思路
  - - DP数组含义
    - 递推公式
    - 初始化
    - 遍历顺序
  - 完整版
  - - DP数组long long溢出问题
- 示例5：两个字符串的删除操作
- - 思路
  - - DP数组含义
    - 递推公式
    - 初始化
  - 完整版
- 示例6：编辑距离
- - 思路
  - - DP数组含义
    - 递推公式
    - 初始化
    - 遍历顺序
  - 完整版
- 总结

单个序列问题

示例1：最长递增子序列（不连续）

300. 最长递增子序列 - 力扣（LeetCode）

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4

示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

1 <= nums.length <= 2500
-10^4 <= nums[i] <= 10^4

思路

一般来说，子序列是不连续的，子数组是连续的。

本题是求不连续的子序列，且要求递增，说明i+1需要用到nums[i]的状态。

DP数组含义

DP数组定义为，以nums[i]为结尾的子序列，最长严格递增长度为dp[i]。

递推公式

递推为：

for(int i=1;i<nums.size();i++){
    for(int j=0;j<i;j++){
        if(nums[i]>nums[j]){
            dp[i]=max(dp[i],dp[j]+1);//这里的递推公式，一定要区分”最长递增子数组“的递推！
        }
    }
}

初始化

初始化直接全部定义为1即可，因为最长递增子序列最短情况为1.

遍历顺序

因为递推公式从左到右递推，i基于i-1的状态，因此是正序遍历

完整版

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        vector<int>dp(nums.size(),1);
        int result=1;
        for(int i=1;i<nums.size();i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j]){
                    dp[i]=max(dp[i],dp[j]+1);
                }
            }
            result=max(result,dp[i]);
        }
        //return dp[nums.size()-1];不能这么写，原因在下面
        return result;
    }
};

注意返回值问题

注意：本题的DP数组定义为”以nums[i]为结尾的序列，其严格递增子序列的长度"，这是因为本题要判断是否递增，因此实际上是对于每一个nums[i]，都进行了nums[i]是否大于j的判断，这个序列是以nums[i]为结尾的，因为递增的判断中i+1一定要用到i的状态。

如果我们将返回值写成

return dp[nums.size()-1];

就会出现如下的情况：

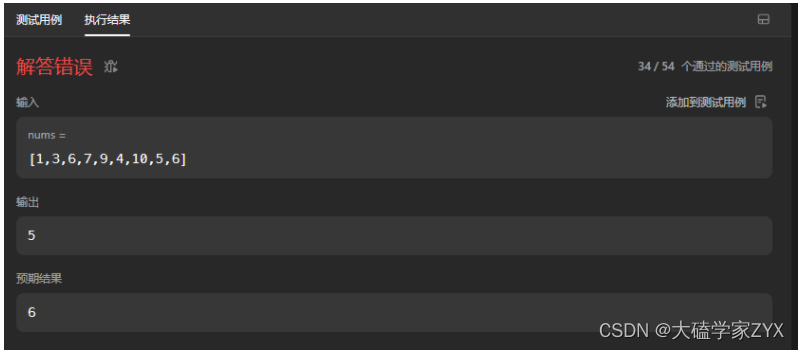
在这里插入图片描述
实际上最长递增序列应该为[1,3,6,7,9,10]，但是如果return最后一个DP数组元素，那么结果就是[1,3,4,5,6]！因为这道题的写法，就是需要以nums[i]为结尾，i+1才能对i的状态进行判断！

因此return必须写为所有DP数组遍历过程中的最大值，即result。

区分示例1：最长递增子数组

给你一个整数数组 nums ，找到其中最长严格递增子数组的长度。

子数组指的是连续的序列。

区别：递推公式

需要特别注意，如果是子数组，那么是连续的结果，递推应该写成：

for(int i=1;i<nums.size();i++){
    if(nums[i]>nums[i-1]){
    	dp[i]=dp[i-1]+1;//DP数组定义也是以Nums[i]为结尾，因为是连续
    }
    result=max(result,dp[i]);
}
return result;

这个公式是求解的连续的递增序列，因此只关注当前元素和它前一个的元素之间的关系，即要求当前元素必须大于它前一个元素。

但是，如果是子序列，子序列是非连续的，我们需要考虑的是当前元素和它之前所有元素之间的关系！如果当前元素大于之前的某个元素，那么当前元素就可以在该元素的基础上构成一个更长的递增子序列。所以，如果是不连续的递增子序列，递推公式应该是：

for(int i=1;i<nums.size();i++){
    for(int j=0;j<i;j++){
        dp[i]=max(dp[i],dp[j]+1);//以Nums[i]为结尾的序列 最长递增子序列长度
    }
    result=max(result,dp[i]);
}
return result;

也就是说，我们在不连续的递增子序列问题中，需要考虑每个元素（nums[i]）与其之前的所有元素（nums[j]）。如果nums[i]大于nums[j]，我们就更新dp[i]为dp[j] + 1和dp[i]中的较大值，这样可以保证**dp[i]始终表示以nums[i]结尾的最长递增子序列的长度**。然后，我们再更新最长递增子序列的长度result。

示例2：最长连续递增序列（连续）

674. 最长连续递增序列 - 力扣（LeetCode）

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

示例 1：

输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例 2：

输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

提示：

1 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9

完整版

本题实际上就是”连续递增子数组“，也就是上面提到的与示例1区分的情况。

lass Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        vector<int>dp(nums.size(),1);
        int res=1;
        for(int i=1;i<nums.size();i++){
            if(nums[i]>nums[i-1]){
                dp[i]=dp[i-1]+1;
            }
            res=max(res,dp[i]);
        }
        return res;
    }
};

示例3：最大子数组和（连续）

53. 最大子数组和 - 力扣（LeetCode）

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4

思路

本题有贪心和DP两种解法，此处只写DP解法，贪心解法见博客：

DAY53：动态规划（十八）最长公共子序列+不相交的线+最大子序列和_大磕学家ZYX的博客-CSDN博客

因为是找具有最大和的连续子数组，那么这个连续子数组一定要包含nums[i]！因此本题DP数组定义依然是”以nums[i]为结尾的连续子数组的和为dp[i]“

DP数组含义

以nums[i]为结尾的连续子数组，最大和为dp[i]

递推公式

以nums[i]为结尾，那么这个连续子数组要么是前面的数组+nums[i]，要么就只有nums[i]自己

for(int i=0;i<nums.size();i++){
    dp[i]=max(dp[i-1]+nums[i],nums[i]);
}

初始化

dp[0]即为Nums[0]，其他均为0

完整版

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        vector<int>dp(nums.size(),0);
        dp[0]=nums[0];
        int result=dp[0];
        for(int i=1;i<nums.size();i++){
            dp[i]=max(dp[i-1]+nums[i],nums[i]);
            result=max(result,dp[i]);
        }
        return result;
    }
};

两个序列之间的问题

两个序列问题的DP数组定义

关于两个序列之间的问题，为了简化初始化，DP数组的定义一般为：以下标i - 1为结尾的A，和以下标j - 1为结尾的B，待求量为dp[i][j]。

也就是说会存在错位，i和j的范围是0--nums.size()。

这个错位操作的目的主要是为了简化初始化这一步，具体可见下面博客：

DAY52：动态规划（十七）子序列问题：最长递增子序列+最长连续递增序列+最长重复子数组_大磕学家ZYX的博客-CSDN博客

初始化操作

像这样的DP数组定义，**dp[0]**就对应着下标-1为结尾的A，实际上代表着空字符串。大多数两序列问题，空字符串对应的DP值都是0，但是当空字符串对应的DP值不为0的时候，就要进行单独的初始化操作。

示例1：最长重复子数组（连续）

718. 最长重复子数组 - 力扣（LeetCode）

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

示例 1：

输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7]
输出：3
解释：长度最长的公共子数组是 [3,2,1] 。

示例 2：

输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0]
输出：5

提示：

1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 100

思路

本题是两个序列的问题，为了简化初始化，我们需要用错位的方法让dp[i]对应的实际上是i-1的值。

本题求解的是子数组，子数组是连续的，因此DP数组的定义必须是nums[i]为结尾！

DP数组含义

以nums1[i-1]，nums2[j-1]为结尾的两个字符串，其公共最长子数组长度为dp[i][j]

递推公式

本题是连续子数组，因此递推如下：

for(int i=1;i<=nums1.size();i++){
    for(int j=1;j<=nums2.size();j++){
        if(nums1[i-1]==nums2[j-1]){
            dp[i][j]=dp[i-1][j-1]+1;//只需要管连续的即可
        }
    }
}

初始化

本题找重复，dp[i][0]和dp[0][j]都表示长度j-1字符串和空字符串的重复长度，直接为0。所以全部初始化为0即可。

遍历顺序

i基于i-1的状态，需要从i-1推过来，所以先填i-1，也就是正序遍历。

完整版

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1,0));
        int result=0;
        for(int i=1;i<=nums1.size();i++){
            for(int j=1;j<=nums2.size();j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                result=max(result,dp[i][j]);
            }
        }
        return result;s
    }
};

示例2：最长公共子序列（不连续）

1143. 最长公共子序列 - 力扣（LeetCode）

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例 3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

提示：

1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。

思路

本题是求不连续序列，不连续序列就比上一题之外多了当前这两个数字不相等的情况。如果当前这两个数字不相等，那么就需要累积之前的所有相等的情况并进行传递！

而且因为本题只是求公共子序列，并没有考虑递增（后一个要看前一个的大小）或者连续（不能在Nums[i]断开），而是如果相等就累积+1，如果不等就继承前面的最大值，因此本题DP数组是”考虑nums[i]在内“的情况！

DP数组含义

以nums1[i-1]，nums2[j-1]为结尾的两个序列内，其最长公共子序列长度为dp[i][j]

递推公式（区分上题）

本题是找不连续的公共子序列，因此递推为：

for(int i=1;i<=nums1.size();i++){
    for(int j=1;j<=nums2.size();j++){
        if(nums1[i-1]==nums2[j-1]){
            dp[i][j]=dp[i-1][j-1]+1;//相等
        }
        else{
            dp[i][j]=max(dp[i-1][j],dp[i][j-1]);//不等，找这两个数据之前累积下来的不连续最大值
        }
    }
}

如果 text1[i-1] 不等于 text2[j-1]，那么最长公共子序列就是 dp[i-1][j]（忽略 text1[i-1]）和 dp[i][j-1]（忽略 text2[j-1]）中的最大值，即 dp[i][j]=max(dp[i-1][j],dp[i][j-1])。因为这里的dp[i-1]是累积结果，而不是最优结果。

初始化

dp[i][0]也是比较这两个字符串分别和空字符串的公共序列，全部都是0。

完整版

class Solution {
public:
    int longestCommonSubsequence(string nums1, string nums2) {
        vector<vector<int>>dp(nums1.size()+1,vector<int>(nums2.size()+1,0));
        for(int i=1;i<=nums1.size();i++){
            for(int j=1;j<=nums2.size();j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[nums1.size()][nums2.size()];
    }
};

注意：递推dp[i-1]进一步理解

动态规划问题中，dp 数组的定义会因具体问题的需要而变化。dp[i] 或 dp[i-1] 不一定总是表示“之前所有的累积结果”，它可能表示到达某一状态的最优解，或者是满足某一条件的某种数量，等等。

例如以下例子：

dp[1][2]=dp[0][1]+1;
dp[2][3]=dp[1][2]+1;

这是在描述某种基于前一个状态的累计，这也是动态规划的一个常见特性。但这不代表所有的 dp[i-1] 或 dp[i] 都代表这样的含义。

以最长递增子序列（LIS）问题为例，我们定义 dp[i] 为以 nums[i] 结尾的最长递增子序列的长度。在这个定义下，dp[i] 并不是前 i-1 个状态的累积结果，而是前 i-1 个状态中，与 nums[i] 形成递增序列的状态的最优结果 +1。这里的 “最优” 指的是长度最大。

这也是动态规划的一大特性：定义状态，然后根据之前的状态来更新当前的状态。根据问题的不同，状态的定义、转移方程的构建也会不同。所以，不是所有的 dp[i-1] 或 dp[i] 都表示“之前所有的累积结果”。

但是，当我们DP数组是”考虑nums[i]在内的最大公共子序列的长度“，那么此时dp[i-1][j-1] 表示的就是之前累积的长度结果。

在动态规划中，根据问题的特点，dp[i-1] 或 dp[i] 可以表示不同的含义，如之前的累积结果，或者之前的最优结果等等。

示例3：判断子序列

392. 判断子序列 - 力扣（LeetCode）

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

致谢：

特别感谢 @pbrother 添加此问题并且创建所有测试用例。

示例 1：

输入：s = "abc", t = "ahbgdc"
输出：true

示例 2：

输入：s = "axc", t = "ahbgdc"
输出：false

提示：

0 <= s.length <= 100
0 <= t.length <= 10^4
两个字符串都只由小写字符组成。

思路

本题有双指针和DP两种做法，双指针做法是一个指向s，一个指向t，t 的指针一直走，s 的指针只有碰到相同字符才走，如果 s 的指针能走到最后，那 s 就是 t 的子序列。

DP的做法，实际上就是在找s和t的最长公共子序列！如果s和t的最长公共子序列长度为s.size()，那么就说明s是t的子序列。

DP数组含义

和最长公共子序列相同，依然是dp[i][j]代表考虑nums1[i-1]和nums2[j-1]以内的最长公共子序列长度。

完整版

class Solution {
public:
    bool isSubsequence(string s, string t) {
        vector<vector<int>>dp(s.size()+1,vector<int>(t.size()+1,0));
        for(int i=1;i<=s.size();i++){
            for(int j=1;j<=t.size();j++){
                if(s[i-1]==t[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j]=dp[i][j-1];//因为只看s在不在t里面，所以只有dp[i][j-1]
                }
            }
        }
        if(dp[s.size()][t.size()]==s.size()){
            return true;
        }
		return false;
    }
};

双指针做法：

一个指针指向s，一个指针指向t，t 的指针一直走，s 的指针只有碰到相同字符才走，如果 s 的指针能走到最后，那 s 就是 t 的子序列。

class Solution {
public:
    bool isSubsequence(string s, string t) {
        int n = s.size(), m = t.size();
        int i = 0, j = 0;
        while (i < n && j < m) {
            if (s[i] == t[j]) {
                i++;
            }
            j++;
        }
        return i == n;
    }
};

进阶做法：

原版DP代码的时间复杂度是O(n*m)（n和m分别是s和t的长度）。

对于进阶问题，当我们有大量的S（即k >= 10亿），我们需要考虑提升我们的代码性能，以便更快地处理大数据。这种情况下，一种有效的方法是利用预处理（preprocessing）的策略，将字符串t的字符位置进行索引，然后对每个s使用二分查找，判断是否是t的子序列。

进阶写法如下：

class Solution {
public:
    bool isSubsequence(string s, string t) {
        // 建立一个二维数组来存放各字符在字符串t中出现的所有位置
        // 这里256是ASCII表的大小，我们假设t和s中的字符都是可打印的ASCII字符
        vector<vector<int>> index(256);
        int m = t.size();

        // 预处理
        for (int i = 0; i < m; i++) {
            // t[i]作为索引，i作为t[i]在字符串t中的位置
            index[t[i]].push_back(i);
        }
        
        // 对于s中的每个字符，进行二分查找，判断其是否在t的对应位置之后出现
        int j = 0;  // 初始化j指向t中的位置
        for (char c : s) {
            if (index[c].size() == 0) return false;  // 如果c没有在t中出现，则s不可能是t的子序列
            int pos = left_bound(index[c], j);  // 找到c在t中的位置大于或等于j的最左位置
            if (pos == index[c].size()) return false;  // 如果没有找到c的位置>=j，说明s不是t的子序列
            j = index[c][pos] + 1;  // 将j更新到下一个待匹配位置
        }
        return true;
    }
    
private:
    // 二分查找，找到第一个大于或等于tar的元素的位置
    int left_bound(vector<int>& arr, int tar) {
        int l = 0, r = arr.size();
        while (l < r) {
            int mid = l + (r - l) / 2;
            if (tar > arr[mid]) l = mid + 1;
            else r = mid;
        }
        return l;
    }
};

这个方法的主要优化在于将t的每个字符的位置信息预处理存储下来，并对字符串s的每个字符进行二分查找，查找其在t中的位置是否满足子序列的条件。这种优化策略利用了预处理和二分查找，将时间复杂度从O(n*m)降低到O(n*log(m))，这里n是字符串s的长度，m是字符串t的长度。

具体来看：

预处理：在预处理步骤中，我们将字符串t中的每个字符的位置信息存储在一个二维数组中，这个过程的时间复杂度是O(m)，其中m是字符串t的长度。这个步骤只需要执行一次，无论我们要判断多少个s是否是t的子序列。
二分查找：对于每个字符串s，我们需要判断其是否是t的子序列。对于s中的每个字符，我们可以在O(log(m))的时间内通过二分查找找到其在t中的位置。因此，对于每个字符串s，我们可以在O(n*log(m))的时间内判断其是否是t的子序列。

所以，如果我们需要判断大量的字符串s是否是t的子序列，那么这种优化策略将会有显著的性能提升。因为预处理步骤只需要执行一次，然后每个s的判断过程中，查找每个字符的时间复杂度都被降低到了O(log(m))。

示例4：不同的子序列

115. 不同的子序列 - 力扣（LeetCode）

给你两个字符串 s 和 t ，统计并返回在 s 的 子序列 中 t 出现的个数。

题目数据保证答案符合 32 位带符号整数范围。

示例 1：

输入：s = "rabbbit", t = "rabbit"
输出：3
解释：
如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。
rabbbit
rabbbit
rabbbit

示例 2：

输入：s = "babgbag", t = "bag"
输出：5
解释：
如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。 
babgbag
babgbag
babgbag
babgbag
babgbag

提示：

1 <= s.length, t.length <= 1000
s 和 t 由英文字母组成

思路

本题最重要的一点是需要理解，从原序列提取子序列的时候，例如原序列s=“bagg”，那么后面的最后两个"g"都可以和前面的"ba"组合成”bag“！

也就是说，即使”ba“只有一组，后面有无数个g，就能够组成无数个"bag"！

DP数组含义

本题DP数组也需要注意，s和t是单独分开找的，dp[i][j]代表以下标i-1为结尾的s里面，以下标j-1为结尾的t的数目！

递推公式

第一种情况，如果相等，那么就要考虑之前的i里面，有多少个能够和目前的"g"配对的”ba"！

if(s[i-1]==t[j-1]){
    dp[i][j]=dp[i-1][j-1]+dp[i-1][j]//[j-1]代表的就是"ba"，[j]代表当前的"g"(累积个数)
}

第二种情况，如果不相等，那么就要继承[i-1]（也就是s前面的部分）里面[j]的个数，继续往下遍历

else{
    dp[i][j]=dp[i-1][j];
}

完整的递推如下：

for(int i=1;i<=s.size();i++){
    for(int j=1;j<=t.size();j++){
        if(s[i-1]==t[j-1]){
            dp[i][j]=dp[i-1][j-1]+dp[i-1][j];//对应"ba"和"g"
        }
        else{
            dp[i][j]=dp[i-1][j];//继承"g"个数
        }
    }
}

初始化

本题初始化也是对dp[i][0]与dp[0][j]分析，也就是说，当i不为0的时候，j对应了空字符串，实际上空字符串就是i的子序列！也就是s中空字符串t的出现次数为1，也就是dp[i][0]=1。

但是dp[0][j]依旧为0，根据题意，空字符串中t出现次数依然是0。

遍历顺序

本题i从i-1推过来，j从j-1推过来，所以是正序遍历。

完整版

class Solution {
public:
    int numDistinct(string s, string t) {
        vector<vector<uint64_t>>dp(s.size()+1,vector<uint64_t>(t.size()+1,0));
        //DP数组含义：长度i-1字符串出现j-1结尾的t的个数是dp[i][j]
        for(int i=0;i<=s.size();i++){
            dp[i][0]=1;
        }
        //int result=0;
        for(int i=1;i<=s.size();i++){
            for(int j=1;j<=t.size();j++){
                if(s[i-1]==t[j-1]){
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j];//"ba"和"g"
                }
                else{
                    dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[s.size()][t.size()];
    }
};

DP数组long long溢出问题

本题存在的问题就是dp数组定义成long long也会超范围，因为计算的有些中间结果，比如前面字符串会有很多“ba”，导致中间结果很大。

因此DP数组需要定义成uint64_t，

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WJUUgBzg-1690901525034)(算法刷题-7.assets/image-20230801171734159.png)]

uint64_t是一个无符号的64位整型，它的取值范围是从0到2^64-1。而long long通常也是64位，但它是有符号的，其取值范围是从**-2^63到263-1**。因此，如果有一个非常大的数（大于2^63-1），long long也溢出了，并且它不能为负，那么**uint64_t就会比long long更适合**。

示例5：两个字符串的删除操作

583. 两个字符串的删除操作 - 力扣（LeetCode）

给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

每步可以删除任意一个字符串中的一个字符。

示例 1：

输入: word1 = "sea", word2 = "eat"
输出: 2
解释: 第一步将 "sea" 变为 "ea" ，第二步将 "eat "变为 "ea"

示例 2:

输入：word1 = "leetcode", word2 = "etco"
输出：4

提示：

1 <= word1.length, word2.length <= 500
word1 和 word2 只包含小写英文字母

思路

本题的思路就是如果相等不做任何操作，如果不相等，要么删第一个字符串，要么删第二个字符串，要么两个都删，把这三种情况进行对比就可以了。

DP数组含义

是否删除需要挨个比对，因此必须是“以nums[i]为结尾”的DP数组定义。而且如果不是这种写法的话，后面递推公式很难推导“删除当前字符”的情况。

以nums1[i-1]为结尾的字符串1，和以nums2[j-1]为结尾的字符串2，达成相等删除的最小次数为dp[i][j]

递推公式

如果相等，什么都不需要做，直接继承删除次数即可

if(word1[i-1]==word2[j-1]){
    dp[i][j]=dp[i-1][j-1];
}

如果不相等，那么三种情况，取删除次数最小值

else{
    //注意是删除次数，删除次数需要+2或者+1！
    dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));
}

初始化

如果word1是空字符串，那么删除次数=word2.size(); 如果word2是空字符串那么同理。

for(int j=0;j<=word2.size();j++){
    dp[0][j]=j;//这里是j而不是word2.size()，因为j是代表了以nums2[j-1]为结尾的长度(也就是最小删除次数)！
}
for(int i=0;i<=word1.size();i++){
    dp[i][0]=i;d
}

完整版

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>>dp(word1.size()+1,vector<int>(word2.size()+1,0));
        for(int i=0;i<=word1.size();i++){
            dp[i][0]=i;//删除次数等于当前长度i
        }
        for(int j=0;j<=word2.size();j++){
            dp[0][j]=j;
        }
        //int result=0;不需要result,因为删除到最后本身就是以最后一个元素为结尾
        for(int i=1;i<=word1.size();i++){
            for(int j=1;j<=word2.size();j++){
                if(word1[i-1]==word2[j-1]){
                    dp[i][j]=dp[i-1][j-1];
                }
                else{
                    dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));
                }
                //result=min(result,dp[i][j]);
            }
        }
		return dp[word1.size()][word2.size()];//因为是两个单词的整体比对，所以最终的删除次数，就是以最后一个元素为结尾
    }
};

示例6：编辑距离

72. 编辑距离 - 力扣（LeetCode）

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

提示：

0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

思路

本题主要是拆分情况，删除的情况是分别删除，增加的情况实际上和删除一样，修改的情况是不相等直接换相等，找这三种情况的最小操作数就可以了！

例如word2删除元素的操作数1，实际上就是word1增加元素的操作数1。因此，我们理解成word2从头到尾都不变也可以！

增加元素的情况，实际上就是把word2那个不相等的元素加到了word1的最后一个。和删掉word2那个不相等的元素，操作数是一样的。

DP数组含义

总的操作数一定是以最后一个元素为结尾的，因此也属于需要挨个处理，最后返回DP数组最末数值的类型。

以word1[i-1]为结尾的字符串和以word2[j-1]为结尾的字符串，令它们相等，所需的最小操作数是dp[i][j]

递推公式

第一种情况不变，那么操作数直接继承。

if(word1[i-1]==word2[j-1]){
    dp[i][j]=dp[i-1][j-1];
}

第二种情况是删除，我们可以理解为word2不变，从头到尾都是word1上面操作。

第三种情况是增加，也就是把word2上面的元素加到word1后面

第四种情况是替换，也就是在上一个操作数的基础上，进行替换操作，直接让word1[i-1]==word2[j-1]

else{
    //删除word1元素
    dp[i][j]=dp[i-1][j]+1;
    //增加word1元素
    dp[i][j]=dp[i][j-1]+1;//也可以理解为删除word2元素
    //替换word1元素
    dp[i][j]=dp[i-1][j-1]+1;
}

初始化

如果word1和空字符串对比，那么次数=word1当前的长度。word2同理。

for(int i=0;i<=word1.size();i++){
   dp[i][0]=i;
}
for(int j=0;j<=word2.size();j++){
    dp[0][j]=j;
}

遍历顺序

因为都是基于i-1和j-1，因此遍历顺序都是从前到后。

完整版

class Solution {
public:
    int minDistance(string word1, string word2) {
        vector<vector<int>>dp(word1.size()+1,vector<int>(word2.size()+1,0));
        for(int i=0;i<=word1.size();i++){
            dp[i][0]=i;
        }
        for(int j=0;j<=word2.size();j++){
            dp[0][j]=j;
        }
        for(int i=1;i<=word1.size();i++){
            for(int j=1;j<=word2.size();j++){
                if(word1[i-1]==word2[j-1]){
                    //一样的话就不变
                    dp[i][j]=dp[i-1][j-1];
                }
                else{
                    //不一样的话，删除/增添/替换word1
                    dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+1));
                }
            }
        }
        return dp[word1.size()][word2.size()];//总的操作数一定是以最后一个元素为结尾的！
    }
};

总结

如果要求的子序列是连续的子序列，那么DP数组含义一定是“以nums[i]为结尾的序列，待求量为dp[i]”
如果不连续但是i+1需要用到i的状态进行判断，例如最长递增子序列，递增的判断需要i的信息，DP数组含义也是“以nums[i]为结尾的序列”
例如不同的子序列、两个字符串删除操作、编辑距离这类题目，不管怎么操作，最后的结果一定是处理完了最后一个元素才能得出，所以DP数组定义也是“以nums[i]为结尾”的情况。
例如最长公共子序列、判断子序列这类题目，要求两个序列的公共序列而且不连续，所以就必须是“考虑nums[i]长度内的所有结果”，因为递推本身存在了累积的过程，所以到了最后一个，就是累积的最大结果值。