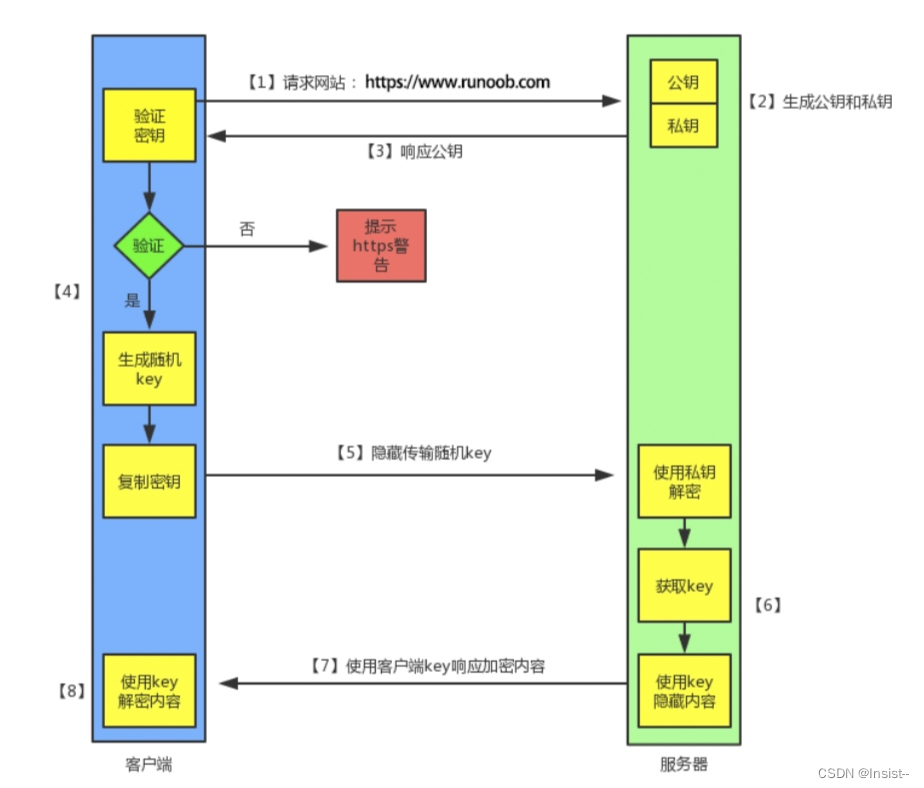
1.概念:
1.顺序存储
顺序存储结构,是指用一段地址连续的存储单元来依次存储结构,如图所示,每个蓝色方块都对应了数组中的一个数据,数据有类型,例如:32位整型int、单精度浮点型float、双精度浮点型double、字符型char、64位整型long long、64位短整型short等等。

2.存储方式
我们通常用一维数组来实现顺序存储结构,将第一个元素存储到索引为0的位置上,把第二个元素存储到索引为1的位置上,以此类推
int[] num=new int[7]//声明长度为7的数组我们也可以将数组中的元素事先初始化
int[] num={5,2,0,1,3,1,4};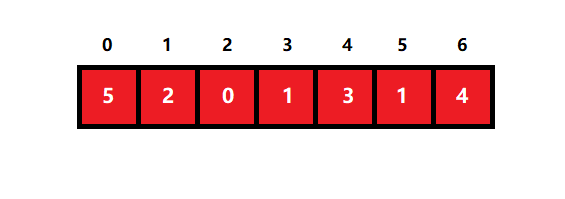
3.长度
数组的长度是不可变的,只要被初始化长度就是固定了,int类型的数组默认初始化为0,boolean数组的默认初始化为false,其他的类型数组的初始值都是该值的默认值
4.数组中的索引
数组中的元素索引,我们可以用[]运算符来完成
int[] num={5,2,0,1,3,1,4};
int a=num[0];//5
int b=a[6];//4
int c=a[7]// 报错a[0]代表的是数组中的第一个元素,a[6]表示的是数组中的最后一个元素,而a[7]则是非法的,因为该数组中的元素的个数是7个。而最大索引值是6,所以a[7]会触发“下标越界的错误”。
5.数组的函数传参
在学习函数的时候,我们知道,如果想将两个整型变量传递给参数,通过函数返回两个整型变量的和,比如:
public int add(int a,int b){
return a+b;
}我们如果要求的是一个长度是10的数组中的所有元素所有和,我们应该如何通过函数来实现呢?例如:
public int add(int[] num){
int sum=0;
for(int i=0;i<num.length;i++){
sum+=num[i];
}
return sum;
}我们利用了一个for循环,将数组中的所有元素都取出来,然后累加到变量sum上,最后返回sum的值就ok了,这里需要知道num.length就是拿到该数组的长度,这一点是非常的关键的
2.题目分析
1.数组中的元素查找
假如给你一个数组num,让你去找到数组中是否包含targrt,如果是的话,返回其索引,没有的话直接返回-1
public int find(int[] num,int target){
int index=-1;
for (int i = 0; i <num.length; i++) {
if(num[i]==target){
index=i;
}
}
return index;
}做题步骤:
- 如果没找到目标元素,返回-1,所以我们在初始化的时候直接给它初始化为-1
- 遍历数组中的每个元素
- 如果找到数组中的某个元素与target相等,则将其索引赋给index
- 最后返回index
2.元素中的最小值查找
假如给你一个数组num,让你去找到数组中最小的值,返回最小值的索引(最大值计算过程相类似,判别条件变一变就行)
public int findMin(int[] num,int target){
int index=0;
int min=0;
for (int i = 0; i <num.length; i++) {
if(num[i]<min){
index=i;
min=num[i];
}
}
return index;
}- 我们先假设数组中第一个元素是最小的
- 开始遍历数组中的全部元素
- 如果数组中的元素num[i]比min小,则更新min值以及对应的index值
leeetcode题单:
搜索旋转排序数组
class Solution {
public int search(int[] nums, int target) {
if(nums==null||nums.length==0){
return -1;
}
int right=nums.length-1;
int left=0;
//二分查找
while(left<=right){
//查找中间值
int mid=left+(right-left)/2;
if(nums[mid]==target){
return mid;}
//中点大于目标值,在数组的右边
if(nums[mid]<nums[right]){
if(target>nums[mid]&&target<=nums[right]){
left=mid+1;
//在数组的左边
}else{
right=mid-1;
}
//目标值在左边
}else{
if(target>=nums[left]&&target<nums[mid]){
right=mid-1;
}else{
left=mid+1;
}
}
}
return -1;
}
}拿硬币
class Solution {
public int minCount(int[] coins) {
if(coins==null||coins.length==0){
return 0;
}
int count=0;
for (int i = 0; i <coins.length; i++) {
count+=(coins[i]&1)==0?(coins[i]/2):((coins[i]/2)+1);
}
return count;
}
}寻找旋转排序数组中的最小值
class Solution {
public int findMin(int[] nums) {
//对入参进行判断
if(nums==null||nums.length==0){
return 0;
}
int n=nums.length;
int left=0;
int right=n-1;
while(left<right){
int mid=left+(right-left)/2;
//最小值永远在无序的那一边,左大于右
if(nums[mid]>nums[right]){
left=mid+1;
}else{
right=mid;
}
}
return nums[left];
}
}山峰数组的顶部
class Solution {
public int peakIndexInMountainArray(int[] num) {
int max=num[0];
int maxIndex=0;
for(int i=0;i<num.length;i++){
if(num[i]>max){
max=num[i];
maxIndex=i;
}
}
return maxIndex;
}
}