1 引言
本项目构建了一个全连接神经网络(FCN),实现对MINST数据集手写数字的识别,没有借助任何深度学习算法库,从原理上理解手写数字识别的全过程,包括反向传播,梯度下降等。
2 全连接神经网络介绍
2.1 什么是全连接神经网络
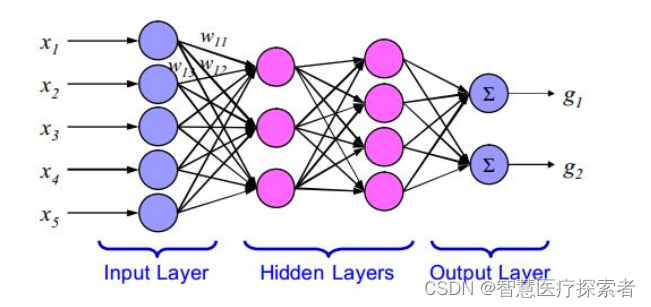
全连接网络(Fully-Connected Network,简称FCN),即在多层神经网络中,第N层的每个神经元都分别与第N-1层的神经元相互连接。如下图便是一个简单的全连接网络:
2.2 损失函数
损失函数(loss function)在深度学习领域是用来计算搭建模型预测的输出值和真实值之间的误差,是一种衡量模型与数据吻合程度的算法。损失函数的值越高预测就越错误,损失函数值越低则预测越接近真实值。对每个单独的观测(数据点)计算损失函数。将所有损失函数(loss function)的值取平均值的函数称为代价函数(cost function),更简单的理解就是损失函数是针对单个样本的,而代价函数是针对所有样本的。
- 损失函数越小越好
- 计算实际输出与目标之间的差距
- 为更新输出提供依据(反向传播)
常见的损失函数
(1)均方误差损失(Mean Squared Error,MSE)
均方误差损失MSE,又称L2 Loss,用于计算模型输出y_hat 和目标值y 之差的均方差。一般用在线性回归中,可以理解为最小二乘法。均方差损失是机器学习、深度学习回归任务中最常用的一种损失函数 。
(2)平均绝对误差(Mean Absolute Error,MAE)
平均绝对误差MAE,又称L1 Loss,是另一种用于回归模型的损失函数。和 MSE 一样,这种度量方法也是在不考虑方向(如果考虑方向,那将被称为平均偏差(Mean Bias Error, MBE),它是残差或误差之和)的情况下衡量误差大小。但和 MSE 的不同之处在于,MAE 需要像线性规划这样更复杂的工具来计算梯度。此外,MAE 对异常值更加稳健,因为它不使用平方。损失范围也是 0 到 ∞。
(3)交叉熵损失函数(Cross Entropy Loss)
交叉熵(Cross Entropy)是Shannon信息论中一个重要概念,主要用于度量两个概率分布间的差异性信息。语言模型的性能通常用交叉熵和复杂度(perplexity)来衡量。交叉熵的意义是用该模型对文本识别的难度,或者从压缩的角度来看,每个词平均要用几个位来编码。Cross Entropy损失函数是分类问题中最常见的损失函数。
2.3 反向传播
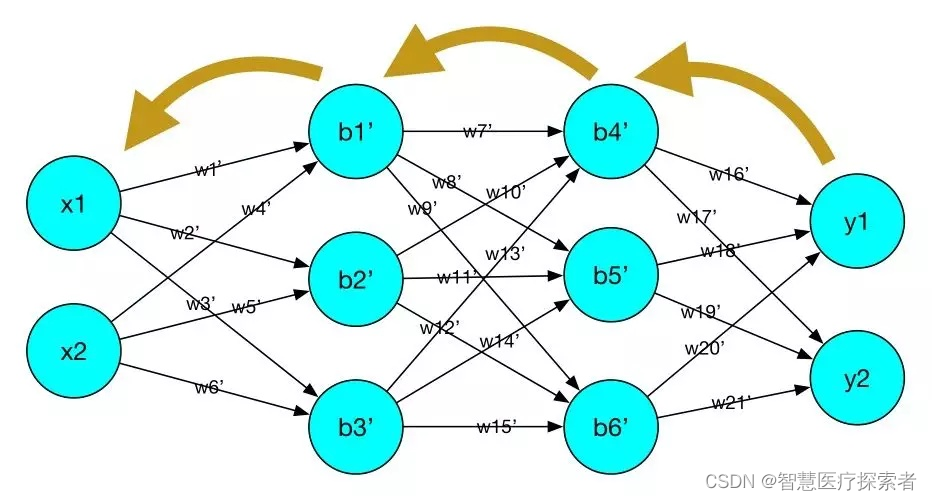
误差反向传播(Back-propagation, BP)算法的出现是神经网络发展的重大突破,也是现在众多深度学习训练方法的基础。该方法会计算神经网络中损失函数对各参数的梯度,配合优化方法更新参数,降低损失函数。BP本来只指损失函数对参数的梯度通过网络反向流动的过程,但现在也常被理解成神经网络整个的训练方法,由误差传播、参数更新两个环节循环迭代组成。
神经网络的训练过程中,前向传播和反向传播交替进行,前向传播通过训练数据和权重参数计算输出结果;反向传播通过导数链式法则计算损失函数对各参数的梯度,并根据梯度进行参数的更新
3 使用FCN实现MNIST手写数字识别
3.1 MINIST数据集介绍
MNIST数据集是美国国家标准与技术研究院收集整理的大型手写数字数据库,包含60,000个示例的训练集以及10,000个示例的测试集。其中的图像的尺寸为28*28。采样数据显示如下:

3.2 FCN识别MINIST数据集代码实现
import torch
from torch import nn
from torchvision import datasets
from torchvision.transforms import transforms
import matplotlib.pyplot as plt
import numpy as np
class MnistNet(nn.Module):
def __init__(self):
super().__init__()
self.layer = nn.Sequential(
# 图片的原尺寸为28*28,转化为784,输入层为784,输出层为256
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 64),
nn.ReLU(),
nn.Linear(64, 16),
nn.ReLU(),
nn.Linear(16, 10),
nn.Softmax(dim=1)
)
def forward(self, x):
x = x.view(-1, 28*28*1)
return self.layer(x)
batchsize = 32
lr = 0.01
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.1307, ), (0.3081,))])
data_train = datasets.MNIST(root="./data/", transform=transform, train=True, download=True)
data_test = datasets.MNIST(root="./data/", transform=transform, train=False)
train_loader = torch.utils.data.DataLoader(data_train, batch_size=batchsize, shuffle=True)
test_loader = torch.utils.data.DataLoader(data_test, batch_size=batchsize, shuffle=False)
if __name__ == '__main__':
model = MnistNet()
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=lr, momentum=0.5)
for i in range(5):
plt.subplot(1, 5, i + 1)
plt.xticks([])
plt.yticks([])
plt.imshow(data_train.data[i], cmap=plt.cm.binary)
plt.show()
lepoch = []
llost = []
lacc = []
epochs = 30
for epoch in range(epochs):
lost = 0
count = 0
for num, (x, y) in enumerate(train_loader, 1):
y_h = model(x)
loss = criterion(y_h, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
lost += loss.item()
count += batchsize
print('epoch:', epoch + 1, 'loss:', lost / count, end=' ')
lepoch.append(epoch + 1)
llost.append(lost / count)
with torch.no_grad():
acc = 0
count = 0
for num, (x, y) in enumerate(test_loader, 1):
y_h = model(x)
_, y_h = torch.max(y_h.data, dim=1)
acc += (y_h == y).sum().item()
count += x.size(0)
test_acc = acc / count * 100
lacc.append(test_acc)
print('acc:', test_acc)
plt.plot(lepoch, llost, label='loss')
plt.plot(lepoch, lacc, label='acc')
plt.legend()
plt.show()3.3 结果输出
经过30个epoch后,在测试集上的准确率达到了97.3%
epoch: 1 loss: 0.0697015597740809 acc: 56.120000000000005
epoch: 2 loss: 0.0542279725531737 acc: 81.2
epoch: 3 loss: 0.051337766939401626 acc: 83.53
epoch: 4 loss: 0.05083678769866626 acc: 84.49
epoch: 5 loss: 0.05052243163983027 acc: 85.09
epoch: 6 loss: 0.05029139596422513 acc: 85.65
epoch: 7 loss: 0.050102355525890985 acc: 86.14
epoch: 8 loss: 0.04994755889574687 acc: 86.02
epoch: 9 loss: 0.0498184863169988 acc: 86.71
epoch: 10 loss: 0.04970114469528198 acc: 86.81
epoch: 11 loss: 0.04792855019172033 acc: 94.86
epoch: 12 loss: 0.047099880089362466 acc: 95.64
epoch: 13 loss: 0.04690476657748222 acc: 96.04
epoch: 14 loss: 0.04677621142864227 acc: 96.32
epoch: 15 loss: 0.046683601369460426 acc: 96.52
epoch: 16 loss: 0.04659009942809741 acc: 96.69
epoch: 17 loss: 0.04652327968676885 acc: 96.72
epoch: 18 loss: 0.04646410925189654 acc: 96.81
epoch: 19 loss: 0.0464125766257445 acc: 96.75
epoch: 20 loss: 0.04636456128358841 acc: 97.07000000000001
epoch: 21 loss: 0.046326734560728076 acc: 96.85000000000001
epoch: 22 loss: 0.04628034559885661 acc: 96.91
epoch: 23 loss: 0.04625135076443354 acc: 97.0
epoch: 24 loss: 0.046217381453514096 acc: 97.14
epoch: 25 loss: 0.046193461724122364 acc: 97.03
epoch: 26 loss: 0.046168098962306975 acc: 97.16
epoch: 27 loss: 0.0461397964378198 acc: 97.27
epoch: 28 loss: 0.0461252645790577 acc: 97.22
epoch: 29 loss: 0.04609716224273046 acc: 97.19
epoch: 30 loss: 0.04608173056840897 acc: 97.3准确率变化曲线如下: