题目来源：https://leetcode.cn/problems/unique-paths-ii/description/

 

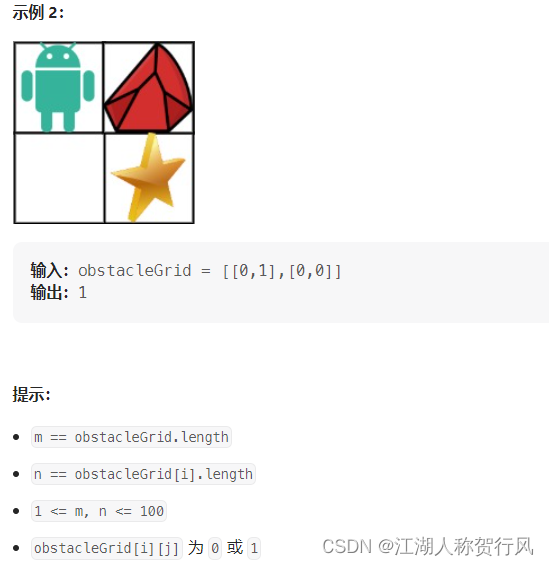
 C++题解：动态规划五部曲。

1. 确定dp数组（dp table）以及下标的含义。dp[i][j] ：表示从(0, 0)出发，到(i, j) 有dp[i][j]条不同的路径。
2. 确定递推公式。递推公式和62.不同路径一样，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。这里需要注意一点，因为有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）。
3. dp数组初始化。dp[0][0] = 1.
4. 确定遍历顺序。从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出，一定是从左到右一层一层遍历，同时要保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。
5. 举例推导dp数组。

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        dp[0][0] = 1;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(obstacleGrid[i][j] == 1) dp[i][j] = 0;
                else {
                    if(i-1 >= 0) dp[i][j] += dp[i-1][j];
                    if(j-1 >= 0) dp[i][j] += dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
};

代码随想录代码：

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size();
        int n = obstacleGrid[0].size();
	if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍，直接返回0
            return 0;
        vector<vector<int>> dp(m, vector<int>(n, 0));
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 1) continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
};