详解顺序表功能

news2024/11/15 15:47:07

前言

随着我们C语言的不断深入学习，我们要开始学习一点数据结构来增加我们的内功了，虽说现在很多高级语言的顺序表，链表等可以不用自己实现，但在C语言中是需要我们自己来实现的，这并不能说明C语言和其他语言比C语言很拉跨，我们通过C语言模拟实现一下这种数据结构可以让我们更加深入理解一个其他语言中我们经常使用的一些内容。当然，我们所要学习的不仅仅是它们的实现，更重要的是它们的思想。

一、顺序表

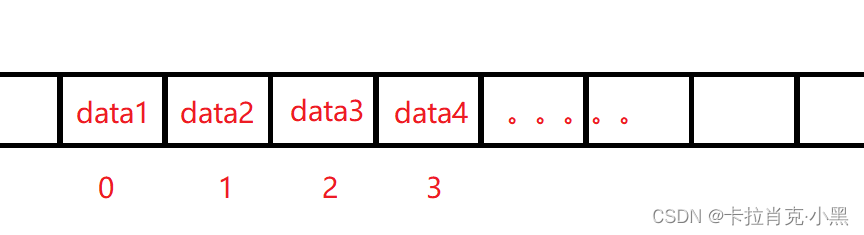
顺序表是在计算机内存中以数组的形式保存的线性表，线性表的顺序存储是指用一组地址连续的存储单元依次存储线性表中的各个元素、使得线性表中在逻辑结构上相邻的数据元素存储在相邻的物理存储单元中。顺序表是将表中的结点依次存放在计算机内存中一组地址连续的存储单元中。
在内存中的存储情况如下：
在这里插入图片描述

二、顺序表的功能

常见的顺序表的功能有增加，删除，查找，修改。还有一些其他的功能：排序，合并，返回元素个数等。
增加：增加可以分为头部增加和尾部增加和指定位置增加，指定位置的增加又可以分为在指定元素左边或右边进行增加。
删除：删除可以分为头部删除和尾部删除和指定位置删除。
查找：顾名思义，查找指定元素或位置。
修改：把指定元素或位置的元素修改为其他元素。
排序：把结构中的数据进行排序。
合并：把多个结构合并为一个。
返回元素个数：把顺序表中的具体的元素个数显示出来。

三、顺序表的实现

顺序表的实现又有静态和动态之分。
静态的顺序表的大小已经固定，而动态顺序表的大小是可以发生变化的，静态的顺序表使用局限性太大，会出现空间浪费和空间不够的尴尬局面。而动态顺序表则解决静态顺序表的问题。但我们还是要学习一下静态顺序表，观察动态和静态的异同点。我们的函数实现都是通过传址进行的，不用传值是避免进行大规模的拷贝，进而造成时间和空间的浪费。

1.顺序表的静态实现

顺序表的创建

#define MAX 10 //存放元素的最大个数
typedef int datatype;//把类型重新命名，方便后面的参数类型的修改，增加代码的鲁棒性
typedef struct SList//定义顺序表的结构体
{
	int position;//表中元素的个数和位置
	datatype arr[MAX];//用来存放元素
}SL;//把结构体类型重新命名为SL

我们实现的是一个简单的顺序表，存储类型是int类型的数据，放在的int类型的数组中。

顺序表的初始化，打印和销毁

void Initialization(SL *sl)//初始话顺序表
{
	assert(sl);//进行断言，防止传入的指针或者地址不合法而造成的错误
	sl->position = 0;//开始没有元素，所以位置为0
}
SL* InitializationList()
{
	SL* sl = (SL*)malloc(sizeof(SL));
	sl->position = 0;
	return sl;
}
void print(const SL *sl)//打印顺序表
{
	assert(sl);//进行断言
	for (int i = 0; i < sl->position; i++)
	{
		printf("%d ", sl->arr[i]);
	}
	printf("\n");
}
void Destroy1(SL* sl)//销毁顺序表
{
	assert(sl);
	sl->position = 0;//把元素个数置为0
}
void Destroy2(SL* sl)//销毁顺序表
{
	assert(sl);
	free(sl);//把空间进行释放
	sl->position = 0;
	sl = NULL;//把指针置空
}

顺序表的初始化有两种，一种是在主函数中创建完成，通过第一个函数进行初始化，一种是在函数中进行创建并且通过返回类型返回给主函数。销毁函数也是针对上面的两种初始化函数而进行设计的，第一个不是动态开辟的，所以不可以用free，第二个是在函数中动态开辟的空间，所以需要free进行释放。防止造成内存泄漏。
这里我们不是静态实现吗？为什么还会用动态开辟呢？
这里的静态是指数据的储存大小是不变的，我们动态开辟的一块结构体所需要的内存是固定不变的，结构体里面数组的大小是固定的，他的存储元素个数和我们结构体是否是动态开辟的无关。和数组大小有关。
我们进行的是传址调用，当我们不需要对元素进行修改时，我们可以加上const进行修饰，防止我们进行修改。

顺序表的增加和删除

我们先看代码的实现：

void Popback(SL* sl, datatype n)//头插
{
	assert(sl);//进行断言
	if (sl->position < MAX )//判断数组中是否还有空间
	{
		int sum = sl->position;//创建一个变量等于数组中插入元素后的位置
		for (; sum > 0; sum--)
		{
			sl->arr[sum] = sl->arr[sum - 1];//把插入元素后的前一个元素向后移动
		}
		sl->arr[sum] = n;//把数组中的一个元素设置为传入的值
		sl->position++;//元素位置向后移动
	}
	else
	{
		printf("空间不足\n");
		return;
	}
}
void Popfornt(SL* sl)//头删
{
	assert(sl);//进行断言
	int sum = 1;
	for (; sum < sl->position; sum++)
	{
		sl->arr[sum - 1] = sl->arr[sum];//把数组中元素进行前移进行覆盖
	}
	sl->position--; //元素位置向前移动
}
void Pushback(SL* sl, datatype n)//尾插
{
	assert(sl);
	if (sl->position < MAX)//判断数组中是否还有空间
	{
		sl->arr[sl->position] = n;//直接在数组后插入元素
		sl->position++;//元素位置向后移动
	}
	else
	{
		printf("空间不足\n");
		return;
	}
}
void Pushfornt(SL* sl)//尾删
{
	assert(sl);
	sl->position--;//直接进行个数减一，表明这个位置可以进行覆盖
}

头插和头删：把元素插入在数组的第一个位置，所以需要第一个位置后面的所有元素向后进行移动，头删则需要把第一个位置后面的所有元素向前覆盖。
尾插和尾删：直接把元素插入在最后位置或者直接对元素个数进行减一达到尾插和尾删的效果。

void test1()//进行头删，尾删，头插，尾插。
{
	SL sl;
	Initialization(&sl);//初始话顺序表
	Popback(&sl, 1);//进行头插
	Popback(&sl, 2);
	Popback(&sl, 3);
	Popback(&sl, 4);
	Popback(&sl, 5);
	printf("头插后：");
	print(&sl);
	Pushback(&sl, 6);//进行尾插
	Pushback(&sl, 7);
	Pushback(&sl, 8);
	Pushback(&sl, 9);
	Pushback(&sl, 10);
	Pushback(&sl, 11);//超过数组中的大小,空间不足
	printf("尾插后：");
	print(&sl);//打印顺序表的元素
	Pushfornt(&sl);//进行尾删
	printf("尾删后：");
	print(&sl);
	Popfornt(&sl);//进行头删
	printf("头删后：");
	print(&sl);
	Destroy1(&sl);
}
int main()
{
	test1();
	return 0;
}

在这里插入图片描述

顺序表的插入，查询和修改

顺序表的插入和修改都依赖于查询功能，所以我们要先实现顺序表的查询，修改我们也可以直接修改我们想修改的下标的元素，但是我们一般不知道我们要修改的下标的元素是什么，所以需要查找功能，如即将要实现的通讯录，这个我们可以通过姓名查找到该人物的下标，进而修改我们的数值。
下面是我们的实现代码：

int Seeklift(const SL *sl, datatype n)//左查找
{
	assert(sl);
	int sum = 0;
	for (sum = 0; sum < sl->position; sum++)
	{
		if (sl->arr[sum] == n)//判断改下标的元素是否和我们所需的元素相同。
		{
			return sum+1;//数组下标从0开始，所以返回位置进行加1
		}
	}
	return -1;
}
int Seekright(const SL *sl, datatype n)//右查找
{
	assert(sl);
	int sum = sl->position-1;
	for (; sum >0; sum--)
	{
		if (sl->arr[sum] == n)
		{
			return sum+1;
		}
	}
	return -1;
}
void Modify(SL *sl, int n, datatype num)//修改
{
	assert(sl);
	sl->arr[n - 1] = num;//把坐标还原为数组的下标
}
void Insertpos(SL* sl, int n, datatype num)//按数组位置插入,在元素左插入
{
	assert(sl);
	//判断数组中是否还有空间
	if (sl->position < MAX)
	{
		int sum = sl->position;//创建一个变量等于数组中插入元素后的位置
		for (; sum > n-1; sum--)//把坐标还原为数组的下标
		{
			sl->arr[sum] = sl->arr[sum - 1];//把插入元素后的前一个元素向后移动
		}
		sl->arr[n-1] = num;//把数组中的一个元素设置为传入的值
		sl->position++;//元素位置向后移动
	}
	else
	{
		printf("空间不足\n");
		return;
	}
}
void Insertright(SL* sl, int n, datatype num)//在元素右插入
{
	assert(sl);
	//判断数组中是否还有空间
	if (sl->position < MAX)
	{
		int sum = sl->position;//创建一个变量等于数组中插入元素后的位置
		for (; sum > n; sum--)//把坐标还原为数组的下标
		{
			sl->arr[sum] = sl->arr[sum - 1];//把插入元素后的前一个元素向后移动
		}
		sl->arr[n] = num;//把数组中的一个元素设置为传入的值
		sl->position++;//元素位置向后移动
	}
	else
	{
		printf("空间不足\n");
		return;
	}
}

查找：我们把查找分为从左查找和从右查找，分别为左边第一个找到我们所需要的数和右边第一个找到我们所需要的数。我们把返回值设为int类型，如果找不到我们返回 -1。只有找到我们所需要的元素时才可以进行修改。
插入：我们分为左边插入和右边插入，左插入和正常插入逻辑一样，所以默认也是左插入，右插入只是边界和左插入不同，代码实现逻辑一模一样。
修改：修改则是通过我们查找到的元素的下标来进行修改的。如果找不到则不能进行修改。
下面是我们的测试函数：

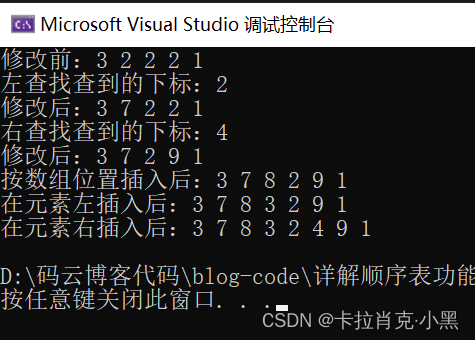
void test2()//进行插入，查询，修改
{
	SL sl;
	Initialization(&sl);//初始话顺序表
	Popback(&sl, 1);//进行头插
	Popback(&sl, 2);
	Popback(&sl, 2);
	Popback(&sl, 2);
	Popback(&sl, 3);
	printf("修改前：");
	print(&sl);
	if (-1 != Seeklift(&sl, 2))//左查找
	{
		printf("左查找查到的下标：%d\n", Seeklift(&sl, 2));
		Modify(&sl, Seeklift(&sl, 2), 7);//修改
		printf("修改后：");
		print(&sl);
	}
	if (-1 != Seekright(&sl, 2))//右查找
	{
		printf("右查找查到的下标：%d\n", Seekright(&sl, 2));
		Modify(&sl, Seekright(&sl, 2), 9);
		printf("修改后：");
		print(&sl);
	}
	Insertpos(&sl, 3, 8);//按数组位置插入
	printf("按数组位置插入后：");
	print(&sl);
	Insertpos(&sl, Seeklift(&sl, 2), 3);//在元素左插入
	printf("在元素左插入后：");
	print(&sl);
	Insertright(&sl, Seeklift(&sl, 2), 4);//在元素右插入
	printf("在元素右插入后：");
	print(&sl);
	Destroy1(&sl);
}
int main()
{
	test2();
	return 0;
}

我们测试的逻辑是先进行头插5个元素，分别进行左右查找并且进行修改，最后在进行左右插入。
在这里插入图片描述

顺序表的升降排序和元素个数的返回

这里的排序我们都是使用的冒泡排序，等到排序章节会改造为算法更优的排序方法。这里的升排序和降排序唯一的区别就是我们判断大小方式的不同。而我们返回元素个数则是直接返回我们结构体元素下标的总位置，这个也是我们元素的总个数。

void Sortmax(SL* sl)//升排序
{
	assert(sl);
	//冒泡排序
	int i, j, temp;
	for (i = 1; i < sl->position; i++)
	{
		for (j = 0; j < sl->position - i; j++)
		{
			if (sl->arr[j] > sl->arr[j + 1])
			{
				temp = sl->arr[j];
				sl->arr[j] = sl->arr[j + 1];
				sl->arr[j + 1] = temp;
			}
		}
	}
}
void Sortmin(SL* sl)//降排序
{
	assert(sl);
	//冒泡排序
	int i, j, temp;
	for (i = 1; i < sl->position; i++)
	{
		for (j = 0; j < sl->position - i; j++)
		{
			if (sl->arr[j] < sl->arr[j + 1])
			{
				temp = sl->arr[j];
				sl->arr[j] = sl->arr[j + 1];
				sl->arr[j + 1] = temp;
			}
		}
	}
}
int Size(const SL *sl)//返回顺序表中元素个数
{
	assert(sl);
	return sl->position;
}

下面是我们的测试代码：

void test3()//进行升降排序
{
	SL* sl;
	sl = InitializationList();//初始话顺序表
	Popback(sl, 1);
	Popback(sl, 5);
	Popback(sl, 3);
	Popback(sl, 4);
	Popback(sl, 2);
	printf("排序前：");
	print(sl);
	Sortmax(sl);//升序排列
	printf("升序后：");
	print(sl);
	Sortmin(sl);//降序排列
	printf("降序后：");
	print(sl);
	printf("元素总个数：%d", Size(sl));
	Destroy2(sl);
}
int main()
{
	test3();
	return 0;
}

在这里插入图片描述
这里我们用的第二种初始化方式，所以进行传参是不需要在加取地址符了。销毁函数也是用的第二个，防止内存泄漏。

顺序表的合并

顺序表的合并我们是进行升序合并的，而且也是两个升序的顺序表进行合并的。
下面是我们的思路：

SL* Merge(const SL* sl1,const SL* sl2)//合并两个有序的顺序表
{
	assert(sl1 && sl2);
	SL* sl = (SL*)malloc(sizeof(SL));
	sl->position = 0;
	int i = 0;//用来访问数组中的元素
	int j = 0;
	while (i < sl1->position &&  j < sl2->position)//当任意一个数组中的元素到达尾部时结束循环
	{
		if (sl1->arr[i] <= sl2->arr[j])//判断数组中的元素大小，谁小谁进行尾插
		{
			Pushback(sl, sl1->arr[i]);
			i++;
		}
		else
		{
			Pushback(sl, sl2->arr[j]);
			j++;
		}
	}
	if (i >= sl1->position)//判断哪一个数组到达了尾部，把没到达尾部的数组元素进行尾插
	{
		while(j < sl2->position)
		{
			Pushback(sl, sl2->arr[j]);
			j++;
		}
	}
	else
	{
		while (i < sl1->position)
		{
			Pushback(sl, sl1->arr[i]);
			i++;
		}
	}
	return sl;
}

合并的思路是先创建一个结构体，然后两个结构体中的数组进行比较，小的一方插入到我们创建的结构体中。然后当一个顺序表的元素用完时，把另一个顺序表中的元素全部插入到我们创建的结构体中。
下面是我们的测试代码：

void test4()//合并两个有序的顺序表
{
	SL *sl;
	SL sl1 = { 3,{1,6,7}};
	SL sl2 = { 3,{2,3,5}};
	printf("s1：");
	print(&sl1);
	printf("s2：");
	print(&sl2);
	sl =  Merge(&sl1, &sl2);//合并两个有序的顺序表
	printf("合并后：");
	print(sl);
	Destroy2(sl);
	Destroy1(&sl1);
	Destroy1(&sl2);
}
int main()
{
	test4();
	return 0;
}

在这里插入图片描述

1.顺序表的动态实现

顺序表的创建

顺序表的动态实现本质是通过指针来实现的。

typedef int datatype;
typedef struct SList//定义顺序表的结构体
{
	datatype* num;//数据类型的指针
	int sz;//数据元素的个数
	int max;//数据元素的最大个数
}TSL;

这里我们把之前的数组改为相应的指针类型，但是额外的加入了一个元素的最大个数，元素的最大个数是用来判断我们当前的存储是否已满，存储满的话就要进行扩容了。

顺序表的初始化，打印和销毁

void InitIalization(TSL* sl)//初始话顺序表
{
	sl->max = 4;//数据初始元素最大为4个
	sl->sz = 0;//数据的起始元素为0个
	sl->num = (datatype*)malloc(sizeof(datatype) * sl->max);
}

这里我们把开始的容量设置为4，当我们元素的个数和我们的容量大小相同时，我们就要进行扩容了。这里我们只写了初始化的代码，打印和销毁代码和静态的实现方式一模一样。

顺序表的增加和删除

void Expansion(TSL* sl)//进行扩容
{
	datatype* sl1 = (datatype*)realloc(sl->num, sizeof(datatype) * (sl->max * 2));
	{
		if (sl1 == NULL)//判断是否开辟空间成功
		{
			perror("sl1 err\n");//开辟失败进行报错
			return;
		}
		else
		{
			sl->num = sl1;
			sl->max *= 2;//更改容量的大小
		}
	}
}
void PopBack(TSL* sl, datatype n)//头插
{
	assert(sl);
	if (sl->sz == sl->max)//判断空间是否已满,满则扩容
	{
		Expansion(&sl);//传递的是sl的地址，不是sl存放的地址
	}
	int i = 0;
	for (i = sl->sz; i > 0; i--)
	{
		sl->num[i] = sl->num[i - 1];//把插入元素后的前一个元素向后移动
	}
	sl->num[0] = n;//把数组中的一个元素设置为传入的值
	sl->sz++;//元素位置向后移动
}

这里我们可以看到，进行增加的代码逻辑和静态的一模一样，只是多了一个扩容的操作。
注意：我们要注意增容可能会失败，所以不能直接用我们的地址，而是先创建一个结构体，创建成功后在把我们的创建赋给我们原结构体。
我们这里只演示了头插的代码，尾插的逻辑和静态一样，只是把判断代码换成是否要扩容的判断。
下面是演示代码：

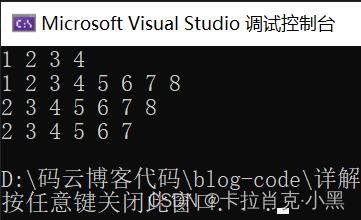
void test5()
{
	TSL sl;
	InitIalization(&sl);//初始话顺序表
	PopBack(&sl, 4);
	PopBack(&sl, 3);
	PopBack(&sl, 2);
	PopBack(&sl, 1);
	Print(&sl);
	PushBack(&sl, 5);
	PushBack(&sl, 6);
	PushBack(&sl, 7);
	PushBack(&sl, 8);
	Print(&sl);
	PopFornt(&sl);
	Print(&sl);
	PushFornt(&sl);
	Print(&sl);
	DEstroy(&sl);
}
int main()
{
	test5();
}

在这里插入图片描述

动态顺序表的总结

动态顺序表只是在判断是否已满的地方多加一个扩容的函数，其他的代码和静态一模一样，思路也一模一样，我们把静态中的数组换为相应的指针，可以通过动态开辟的方式来进行增容。我们的增容是对结构体中的指针进行增容，而非对结构体本身进行增容。

1.顺序表的动态代码

动态测试代码

//main1.c 动态测试代码
#include"main1.h"
void test5()
{
	TSL sl;
	InitIalization(&sl);//初始话顺序表
	PopBack(&sl, 4);
	PopBack(&sl, 3);
	PopBack(&sl, 2);
	PopBack(&sl, 1);
	Print(&sl);
	PushBack(&sl, 5);
	PushBack(&sl, 6);
	PushBack(&sl, 7);
	PushBack(&sl, 8);
	Print(&sl);
	PopFornt(&sl);
	Print(&sl);
	PushFornt(&sl);
	Print(&sl);
	DEstroy(&sl);
}
void test6()
{
	TSL sl;
	InitIalization(&sl);//初始话顺序表
	PopBack(&sl, 3);
	PopBack(&sl, 2);
	PopBack(&sl, 2);
	PopBack(&sl, 2);
	PopBack(&sl, 1);
	Print(&sl);
	if (-1 != SeekLift(&sl, 2))//左查找
	{
		printf("%d\n", SeekLift(&sl, 2));
		MODify(&sl, SeekLift(&sl, 2), 20);//修改
		Print(&sl);
	}
	if (-1 != SeekRight(&sl, 2))//右查找
	{
		printf("%d\n", SeekRight(&sl, 2));
		MODify(&sl, SeekRight(&sl, 2), 200);
		Print(&sl);
	}
	InsertPos(&sl, 3, 8);//按数组位置插入
	Print(&sl);
	InsertPos(&sl, SeekLift(&sl, 2), 33);//在元素左插入
	Print(&sl);
	InsertRight(&sl, SeekLift(&sl, 2), 44);//在元素右插入
	Print(&sl);
	printf("%d\n", SIze(&sl));
	DEstroy(&sl);
}
void test7()
{
	TSL sl;
	InitIalization(&sl);//初始话顺序表
	PopBack(&sl, 1);
	PopBack(&sl, 5);
	PopBack(&sl, 3);
	PopBack(&sl, 4);
	PopBack(&sl, 2);
	Print(&sl);
	SortMax(&sl);//升序排列
	Print(&sl);
	SortMin(&sl);//降序排列
	Print(&sl);
	DEstroy(&sl);
}
void test8()
{
	TSL* sl;
	TSL sl1;
	InitIalization(&sl1);//初始话顺序表
	TSL sl2;
	InitIalization(&sl2);//初始话顺序表
	PushBack(&sl1, 1);
	PushBack(&sl1, 6);
	PushBack(&sl1, 7);
	PushBack(&sl2, 2);
	PushBack(&sl2, 3);
	PushBack(&sl2, 5);
	Print(&sl1);
	Print(&sl2);
	sl = MErge(&sl1, &sl2);//合并两个有序的顺序表
	Print(sl);
	DEstroy(sl);
	DEstroy(&sl1);
	DEstroy(&sl2);
}
int main()
{
	test5();
	test6();
	test7();
	test8();
	return 0;
}

动态实现头文件

//main1.h  动态头文件
#pragma once
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#define MAX 10
typedef int datatype;
typedef struct SList//定义顺序表的结构体
{
	datatype* num;//数据类型的指针
	int sz;//数据元素的个数
	int max;//数据元素的最大个数
}TSL;
void InitIalization(TSL* sl);//初始话顺序表
void PopBack(TSL* sl, datatype n);//头插
void PopFornt(TSL* sl);//头删
void PushBack(TSL* sl, datatype n);//尾插
void PushFornt(TSL* sl);//尾删
int SeekLift(const TSL* sl, datatype n);//左查找
int SeekRight(const TSL* sl, datatype n);//右查找
void MODify(TSL* sl, int n, datatype num);//修改
void InsertPos(TSL* sl, int n, datatype num);//按数组位置插入,在元素左插入
void InsertRight(TSL* sl, int n, datatype num);//在元素右插入
void SortMax(TSL* sl);//升排序
void SortMin(TSL* sl);//降排序
int SIze(const TSL* sl);//返回顺序表中元素个数
TSL* MErge(TSL* sl1, TSL* sl2);//合并两个有序的顺序表
void Print(const TSL* sl);//打印顺序表
void DEstroy(TSL* sl);//销毁顺序表

动态具体函数的实现

//test1.c  动态具体函数的实现
#include"main1.h"
void InitIalization(TSL* sl)//初始话顺序表
{
	sl->max = 4;//数据初始元素最大为4个
	sl->sz = 0;//数据的起始元素为0个
	sl->num = (datatype*)malloc(sizeof(datatype) * sl->max);
}
void Expansion(TSL* sl)//进行扩容
{
	datatype* sl1 = (datatype*)realloc(sl->num, sizeof(datatype) * (sl->max * 2));
	{
		if (sl1 == NULL)//判断是否开辟空间成功
		{
			perror("sl1 err\n");//开辟失败进行报错
			return;
		}
		else
		{
			sl->num = sl1;
			sl->max *= 2;//更改容量的大小
		}
	}
}
void PopBack(TSL* sl, datatype n)//头插
{
	assert(sl);
	if (sl->sz == sl->max)//判断空间是否已满,满则扩容
	{
		Expansion(sl);
	}
	int i = 0;
	for (i = sl->sz; i > 0; i--)
	{
		sl->num[i] = sl->num[i - 1];//把插入元素后的前一个元素向后移动
	}
	sl->num[0] = n;//把数组中的一个元素设置为传入的值
	sl->sz++;//元素位置向后移动
}
void PopFornt(TSL* sl)//头删
{
	assert(sl);
	int i = 0;
	for (i = 0; i < sl->sz; i++)
	{
		sl->num[i] = sl->num[i + 1];
	}
	sl->sz--;
}
void PushBack(TSL* sl, datatype n)//尾插
{
	assert(sl);
	if (sl->sz == sl->max)
	{
		Expansion(sl);
	}
	sl->num[sl->sz] = n;
	sl->sz++;
}
void PushFornt(TSL* sl)//尾删
{
	assert(sl);
	sl->sz--;
}
int SeekLift(const TSL* sl, datatype n)//左查找
{
	assert(sl);
	int i = 0;
	for (i = 0; i < sl->sz; i++)
	{
		if (sl->num[i] == n)
		{
			return i + 1;//数组下标从0开始，所以返回位置进行加1
		}
	}
	return -1;
}
int SeekRight(const TSL* sl, datatype n)//右查找
{
	assert(sl);
	int i = sl->sz - 1;
	for (; i > 0; i--)
	{
		if (sl->num[i] == n)
		{
			return i + 1;
		}
	}
	return -1;
}
void MODify(TSL* sl, int n, datatype num)//修改
{
	assert(sl);
	sl->num[n - 1] = num;
}
void InsertPos(TSL* sl, int n, datatype num)//按数组位置插入,在元素左插入
{
	assert(sl);
	//判断数组中是否还有空间
	if (sl->sz == sl->max)
	{
		Expansion(sl);
	}
	int sum = sl->sz;//创建一个变量等于数组中插入元素后的位置
	for (; sum > n - 1; sum--)//把坐标还原为数组的下标
	{
		sl->num[sum] = sl->num[sum - 1];//把插入元素后的前一个元素向后移动
	}
	sl->num[n - 1] = num;//把数组中的一个元素设置为传入的值
	sl->sz++;//元素位置向后移动
}
void InsertRight(TSL* sl, int n, datatype num)//在元素右插入
{
	assert(sl);
	//判断数组中是否还有空间
	if (sl->sz == sl->max)
	{
		Expansion(sl);
	}
	int sum = sl->sz;//创建一个变量等于数组中插入元素后的位置
	for (; sum > n ; sum--)//把坐标还原为数组的下标
	{
		sl->num[sum] = sl->num[sum - 1];//把插入元素后的前一个元素向后移动
	}
	sl->num[n] = num;//把数组中的一个元素设置为传入的值
	sl->sz++;//元素位置向后移动
}
void SortMax(TSL* sl)//升排序
{
	assert(sl);
	//冒泡排序
	int i, j, temp;
	for (i = 1; i < sl->sz; i++)
	{
		for (j = 0; j < sl->sz - i; j++)
		{
			if (sl->num[j] > sl->num[j + 1])
			{
				temp = sl->num[j];
				sl->num[j] = sl->num[j + 1];
				sl->num[j + 1] = temp;
			}
		}
	}
}
void SortMin(TSL* sl)//降排序
{
	assert(sl);
	//冒泡排序
	int i, j, temp;
	for (i = 1; i < sl->sz; i++)
	{
		for (j = 0; j < sl->sz - i; j++)
		{
			if (sl->num[j] < sl->num[j + 1])
			{
				temp = sl->num[j];
				sl->num[j] = sl->num[j + 1];
				sl->num[j + 1] = temp;
			}
		}
	}
}
int SIze(const TSL* sl)//返回顺序表中元素个数
{
	assert(sl);
	return sl->sz;
}
TSL* MErge(TSL* sl1, TSL* sl2)//合并两个有序的顺序表
{
	assert(sl1 && sl2);
	TSL* sl = (TSL*)malloc(sizeof(TSL));
	if (sl == NULL)//判断是否为空
	{
		perror("malloc: ");//报错且退出
		return;
	}
	InitIalization(sl);
	int i = 0;//用来访问数组中的元素
	int j = 0;
	while (i < sl1->sz && j < sl2->sz)//当任意一个数组中的元素到达尾部时结束循环
	{
		if (sl1->num[i] <= sl2->num[j])//判断数组中的元素大小，谁小谁进行尾插
		{
			if (sl->sz == sl->max)
			{
				Expansion(sl);
			}
			PushBack(sl, sl1->num[i]);
			i++;
		}
		else
		{
			if (sl->sz == sl->max)
			{
				Expansion(sl);
			}
			PushBack(sl, sl2->num[j]);
			j++;
		}
	}
	if (i >= sl1->sz)//判断哪一个数组到达了尾部，把没到达尾部的数组元素进行尾插
	{
		while (j < sl2->sz)
		{
			if (sl->sz == sl->max)
			{
				Expansion(sl);
			}
			PushBack(sl, sl2->num[j]);
			j++;
		}
	}
	else
	{
		while (i < sl1->sz)
		{
			if (sl->sz == sl->max)
			{
				Expansion(sl);
			}
			PushBack(sl, sl1->num[i]);
			i++;
		}
	}
	return sl;
}
void Print(const TSL* sl)//打印顺序表
{
	int i = 0;
	for (i = 0; i < sl->sz; i++)
	{
		printf("%d ", sl->num[i]);
	}
	printf("\n");
}
void DEstroy(TSL* sl)//销毁顺序表
{
	assert(sl);
	free(sl->num);
	sl->num = NULL;
	sl->max = 0;
	sl->sz = 0;
}

总结

大家可以对比一下静态和动态的区别，动态只是在静态的基础上稍稍的进行一下改进，增加一个扩容的函数，其他的一模一样，我们下一个将会用一个小项目来加深我们顺序表印象，这是我们的第一个数据结构，我们还要用它和后面的链表进行对比。学习每个结构的优缺点，是我们在不同问题上选择最优的方案。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/821311.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

AP AUTOSAR在软件定义汽车生态系统中的角色

AP AUTOSAR在软件定义汽车生态系统中的角色

AP AUTOSAR在软件定义汽车生态系统中的角色 AP AUTOSAR是AUTOSAR（汽车开放系统架构）的最新版本之一，它是一种面向服务的软件平台，旨在满足未来汽车电子系统的需求，特别是高性能计算、高带宽通信、软件无线更新（OTA）等方面。 AP AUTOSAR在软件定义汽车生态系统中扮演着…
阅读更多...
【以图搜图】Python实现根据图片批量匹配(查找)相似图片

【以图搜图】Python实现根据图片批量匹配(查找)相似图片

目的&#xff1a;可以解决在本地实现根据图片查找相似图片的功能 背景&#xff1a;由于需要查找别人代码保存的图像的命名&#xff0c;但由于数据集是cifa10图像又小又多&#xff0c;所以直接找很费眼睛&#xff0c;所以实现用该代码根据图像查找图像&#xff0c;从而得到保存…
阅读更多...
azure刷新令牌失效 The grant was issued for a different client id

azure刷新令牌失效 The grant was issued for a different client id

博主在以msal-node这个认证库实现electron客户端混合h5授权登录后&#xff0c;在某一次访问令牌过期后并且通过已存储的刷新令牌获取新的访问令牌和刷新令牌时&#xff0c;在控制台日志看到了The grant was issued for a different client id报错。 Error refreshing token: Se…
阅读更多...
产品经理都在收藏的10个原型设计工具！

产品经理都在收藏的10个原型设计工具！

在产品经理的设计工作中&#xff0c;原型工具是必不可少的&#xff0c;今天本文将会为大家分享8个好用的原型工具&#xff0c;助力产品经理实现高效设计&#xff0c;一起来看看吧&#xff01; 1、即时设计 即时设计是一款优秀的原型工具&#xff0c;它可以在网页中直接运行并…
阅读更多...
CS162 13-17 虚拟内存

CS162 13-17 虚拟内存

起源 为啥我们需要虚拟内存-----------需求是啥&#xff1f; 可以给程序提供一个统一的视图&#xff0c;比如多个程序运行同一个代码段的话&#xff0c;同一个kernel&#xff0c;就可以直接共享 cpu眼里的虚拟内存 无限内存的假象 设计迭代过程 为啥这样设计&#xff1f; 一…
阅读更多...
P2404 自然数的拆分问题

P2404 自然数的拆分问题

题目 思路 最简单的dfs题之一 只需要一点点小优化 代码 #include<bits/stdc.h> using namespace std; const int maxn55; int n; int ans[maxn],s; void print(int tot) { for(int i1;i<tot-1;i) cout<<ans[i]<<""; cout<<ans[tot-1]&…
阅读更多...
Spark-任务怎么切分

Spark-任务怎么切分

&#xff08;1&#xff09;Application&#xff1a;初始化一个SparkContext即生成一个Application&#xff1b; &#xff08;2&#xff09;Job&#xff1a;一个Action算子就会生成一个Job&#xff1b; &#xff08;3&#xff09;Stage&#xff1a;Stage等于宽依赖的个数加1&…
阅读更多...
速成版-带您2天学完vue3框架+Element-plus框架

速成版-带您2天学完vue3框架+Element-plus框架

Vue是渐进式的JavaScript框架&#xff0c;易学易用&#xff0c;性能出色&#xff0c;适用场景丰富的web前端框架&#xff0c;vue算是目前最火的web前端框架之一&#xff0c;使用vue可以提升开发体验。Vue组件可以按照两种不同的风格写&#xff0c;即选项式api和组合式api两种。…
阅读更多...
数据中心电子电气设备常见的五种地线种类和做法

数据中心电子电气设备常见的五种地线种类和做法

数据中心机房计算机系统的集成化程度很高&#xff0c;其正常工作对环境的要求很严格。接地&#xff0c;是指电力系统和电气装置的中性点、电气设备的外露导电部分和装置外导电部分经由导体与大地相连。其作用主要是防止人身遭受电击、设备和线路遭受损坏、预防火灾和防止雷击、…
阅读更多...
7.复合类型注解

7.复合类型注解

目录 1 联合类型 2 交叉类型 2.1 基本使用 2.2 与继承的区别 1 联合类型 联合类型是 或 的关系 联合类型表示这个变量可以是多个类型&#xff0c;比如 a 可以是 数字或字符串 使用联合类型后改变到指定的类型就不会报错了 2 交叉类型 2.1 基本使用 交叉类型是 …
阅读更多...
MB21 手工创建关于生产订单的预留

MB21 手工创建关于生产订单的预留

1、前面博文中有说到新增了工单超领的移动类型Z61，我们在创建新的移动类型的时候参考的是261的移动类型。本质上Z61的配置和261也是一样的。 2、我们在MB21创建预留的时候就会遇到问题 这里系统给出了提示：不能手工创建该类型的预留。 3、SE38对程序进行修改，根据报错的信…
阅读更多...
Qt应用开发(基础篇)——布局管理 Layout Management

Qt应用开发(基础篇)——布局管理 Layout Management

目录 一、前言 二&#xff1a;相关类 三、水平、垂直、网格和表单布局 四、尺寸策略 一、前言 在实际项目开发中&#xff0c;经常需要使用到布局&#xff0c;让控件自动排列&#xff0c;不仅节省控件还易于管控。Qt布局系统提供了一种简单而强大的方式来自动布局小部件中的…
阅读更多...
docker 容器引擎基础（2）

docker 容器引擎基础（2）

目录 创建私有仓库 将修改过的nginx镜像做标记封装&#xff0c;准备上传到私有仓库 将镜像上传到私有仓库 从私有仓库中下载镜像到本地 CPU使用率 CPU共享比例 CPU周期限制 CPU 配额控制参数的混合案例 内存限制 Block IO 的限制 限制bps 和iops 创建私有仓库 仓库&a…
阅读更多...
一起学SF框架系列5.12-spring-beans-数据绑定dataBinding

一起学SF框架系列5.12-spring-beans-数据绑定dataBinding

数据绑定有助于将用户输入动态绑定到应用程序的域模型&#xff08;或用于处理用户输入的任何对象&#xff09;&#xff0c;主要用于web层&#xff0c;但实际可用于任何层。Spring提供了DataBinder来做到这一点&#xff0c;并提供了Validator进行数据验证&#xff0c;两者组成了…
阅读更多...
高通滤波器，低通滤波器

高通滤波器，低通滤波器

1.高通滤波器是根据像素与邻近像素的亮度差值来提升该像素的亮度。 import cv2 import numpy as np from scipy import ndimagekernel_3_3 np.array([[-1,-1,-1],[-1,8,-1],[-1,-1,-1]]) print(kernel_3_3) kernel_5_5 np.array([[-1,-1,-1,-1,-1],[-1,1,2,1,-1],[-1,2,4,2,-…
阅读更多...
网络安全进阶学习第八课——信息收集

网络安全进阶学习第八课——信息收集

文章目录 一、什么是信息收集&#xff1f;二、信息收集的原则三、信息收集的分类1.主动信息收集2.被动信息收集 四、资产探测1、Whois查询#常用网站&#xff1a; 2、备案信息查询#常用网站&#xff1a; 3、DNS查询#常用网站&#xff1a; 4、子域名收集#常用网站&#xff1a;#常…
阅读更多...
在访问一个网页时弹出的浏览器窗口,如何用selenium 网页自动化解决？

在访问一个网页时弹出的浏览器窗口,如何用selenium 网页自动化解决？

相信大家在使用selenium做网页自动化时&#xff0c;会遇到如下这样的一个场景&#xff1a; 在你使用get访问某一个网址时&#xff0c;会在页面中弹出如上图所示的弹出框。 首先想到是利用Alert类来处理它。 然而&#xff0c;很不幸&#xff0c;Alert类处理的结果就是没有结果…
阅读更多...
SNAT和DNAT原理与应用

SNAT和DNAT原理与应用

iptables的备份和还原 1.写在命令行当中的都是临时配置。 2.把我们的规则配置在 备份&#xff08;导出&#xff09;&#xff1a;iptables-save > /opt/iptables.bak 默认配置文件&#xff1a;/etc/sysconfig/iptables 永久配置&#xff1a;cat /opt/iptables.bak > /etc…
阅读更多...
最近安全事件频发，分享一些如何在Sui上构建安全应用的建议

最近安全事件频发，分享一些如何在Sui上构建安全应用的建议

在Sui上构建任何应用程序的一个关键部分是防止恶意攻击和威胁行为。对安全性的重视对于减少用户的资产损失&#xff0c;以及降低对开发者和企业的声誉损害至关重要。 Sui安全和密码学社区的成员总结了一些开发者在开发过程中应该注意避免的最佳实践。虽然其中一些经验是单独针…
阅读更多...
AD21 PCB设计的高级应用（十）Gerber文件转PCB

AD21 PCB设计的高级应用（十）Gerber文件转PCB

&#xff08;十&#xff09;Gerber文件转PCB Altium Designer 导入 Gerber 并转换成 PCB 的操作步骤如下: (1)打开 Altium Designer 软件,执行菜单栏中“文件”→“新的”→“项目”命令,新建一个 PCB Project,并且新建一个 CAM 文档添加到工程中,如图所示。 (2)Gerber 文件有两…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023