647. 回文子串

1.动态规划和2.中心扩展
这个视频是基于上面的视频的代码

方法1:动态规划
布尔类型的dp[i][j]：表示区间范围[i,j] （注意是左闭右闭）的子串是否是回文子串，如果是dp[i][j]为true，否则为false。
dp[i][j] = (c[i] = c[j]) &&( (j-i<=2) || dp[i+1][j-1] );
在这里插入图片描述

class Solution {
    public int countSubstrings(String s) {
    char[] c = s.toCharArray();
    int n = c.length;
    boolean[][] dp = new  boolean[n][n];
    int count =0;

    for(int j=0;j<n;j++){
        for(int i=0;i<=j;i++){
         dp[i][j] = (c[i] == c[j]) &&( (j-i<=2) || dp[i+1][j-1] );

         if(dp[i][j]) count++;
        }
    }
return count;
    }
}

方法2:中心扩展法
只有两种情况：1.以单个字母为中心 2. 以两个字母为中心
在这里插入图片描述

class Solution {
    int count =0;
    public int countSubstrings(String s) {
    for(int i=0;i<s.length();i++){
        helper(s,i,i);
        helper(s,i,i+1);
    }
    return count;
    }

    public void helper(String s, int left, int right){
        while(left>=0&&right<s.length()&&s.charAt(left) == s.charAt(right)){
            count++;
            left--;
            right++;
        }
    }
}

516.最长回文子序列

两种思路：

思路一：求当前序列和反转之后的最长公共子序列
就是这道题1146一摸一样了
dp[i][j] 表示s1的前i个字符和s2的前j个字符最长…

class Solution {
    public int longestPalindromeSubseq(String s) {
    char[] A = s.toCharArray();
    char[] B = new char[A.length];

    for(int i=0;i<A.length;i++){
        B[i] = A[A.length -1-i];
    }

    int[][] dp = new int[A.length+1][A.length+1];

    for(int i=1;i<=A.length;i++){
        for(int j =1;j<=A.length;j++){
            if(A[i-1] == B[j-1]){
                dp[i][j] = dp[i-1][j-1]+1;
            }else{
                dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
    }
 return dp[A.length][B.length];

    }
}

思路二：区间DP
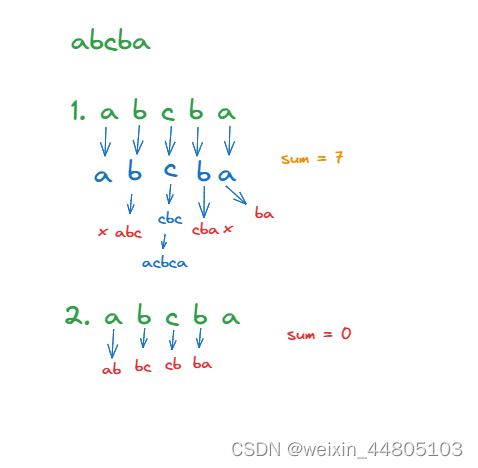
子序列的本质就是选与不选
dp[i][j]：字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。

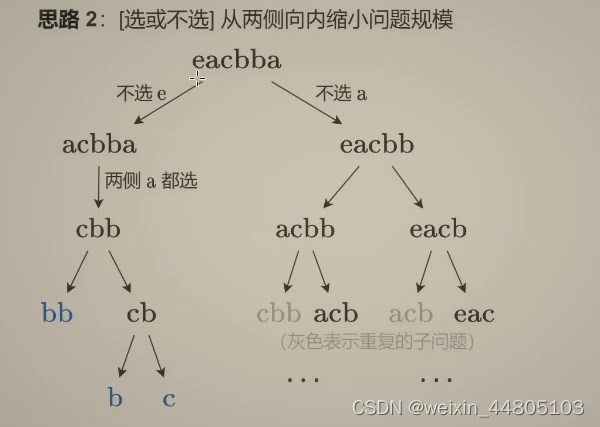
在这里插入图片描述

超出时间限制的递归
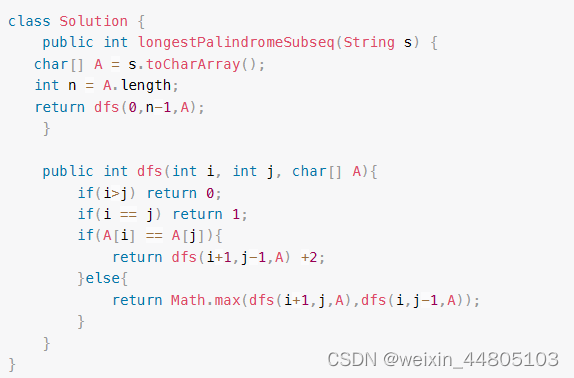
在这里插入图片描述

将递归变成循环：

class Solution {
    public int longestPalindromeSubseq(String s) {
   char[] A = s.toCharArray();
   int n = A.length;
   int[][] dp = new int[n][n];
  
  for(int i = n-1;i>=0;i--){
      dp[i][i] =1;  //2. i==j 
      for(int j=i+1;j<n;j++){ //3.j>i
      
          if(A[i]== A[j]){
              dp[i][j] = dp[i+1][j-1]+2;
          }else{
              dp[i][j] = Math.max(dp[i+1][j],dp[i][j-1]);
          }
      }
  }
 return dp[0][n-1];
    }
}