Android 3D 魔方游戏的设计与开发

5.1 Feature 定义

魔方是一个有趣的益智游戏，相信很多人都玩过。本次毕业设计，欲完成的主要的功能如下：

（1）开始游戏：开始一个新的游戏

（2）返回游戏：当游戏已经开始，“开始游戏”按钮将不可用，玩家可通过“返回游戏”按钮进入先前的游戏界面。

（3）游戏记录：保存玩家的游戏记录，包括排名、玩家姓名、还原魔方所用时间、还原所用的步骤、游戏的日期。

（4）游戏说明：介绍游戏的操作方法及各个菜单

（5）退出游戏：结束游戏

（6）整体旋转：玩家在任一时刻可以同时看到魔方的三个面，玩家可通过旋转按钮或在魔方外区域滑动使魔方整体旋转，使玩家对魔方整体情况有个了解。

（7）单层旋转：玩家在魔方上滑动可对魔方进行每一层的旋转。

（8）游戏计时：玩家刚进入游戏时，如果进行整体的翻转，则不算时间；如果是单层旋转则开始计时，这时，如果进行整体旋转也算入用时。但游戏期间如果切换到其它界面，则暂停计时。

（9）开关按钮：游戏界面设置七个图片按钮，最左上角的为开关按钮，点击它可以打开或关闭其它 6 个按钮。

（10）菜单按钮：点击菜单按钮可弹出游戏菜单

（11）放大与缩小按钮：对魔方的大小进行调整

（12）翻转按钮：由于屏幕大小或玩家的操作习惯不同，故加入此按钮，使玩家对魔方的整体翻转有更多的选择。

（13）重新开始：将魔方还原到原始的状态，重新开始游戏，用时及步数重新开始计算。

（14）随机打乱：将一个魔方随机地转动若干次，旋转次数可由玩家设定。

（15）自动还原：将一个打乱的魔方还原

（16）回主菜单：返回到游戏的主菜单界面

（17）游戏设置：对游戏进行设置，如整体翻转和单层旋转的速度，随机打乱的步数、是否显示计时栏。

（18）关于游戏：关于游戏的一些信息，如版本号、作者、版权等

5.2 类的设计

代码统计

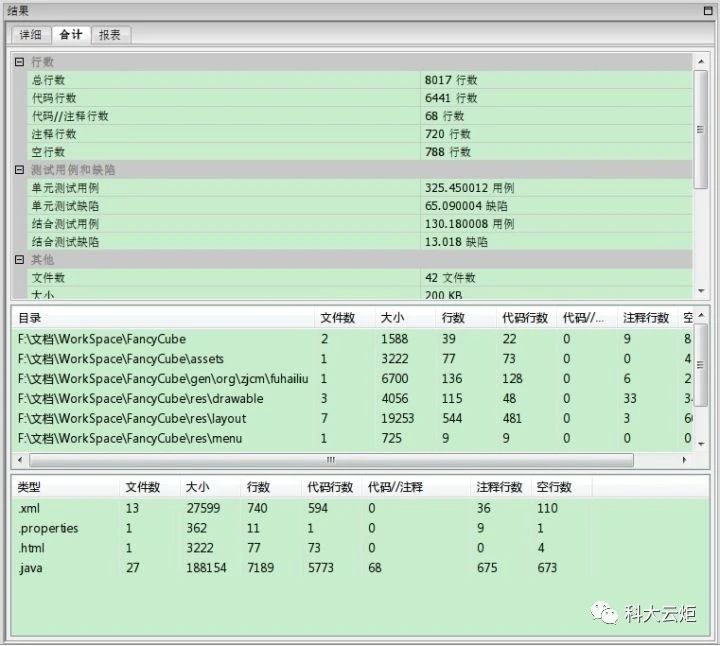
编辑切换为居中

添加图片注释，不超过 140 字（可选）

About: 游戏的关于页面

Color: 颜色类，用于给魔方上色

Cube: 立方体，一个三阶魔方由 27 个小立方体组成

DataBaseAdapter: 数据库接口

DataBaseBean: 封装好的数据库操作类

Face: 面，每个立方体都有 6 个面

FancyCube: 程序的入口点，负责绘制主菜单界面

GameMain: 游戏的主类，主要负责游戏场景的构建、坐标的转换、魔方旋转、保存设置与加载设置、游戏状态的判断等

GameRecord: 显示、保存与删除游戏戏记录

Gesture: 手势判断

Help: 游戏说明

Layer: 层，一个三阶魔方由 9 个层构成

Matrix: 矩阵，点与矩阵的乘法、矩阵与矩阵的乘法

MatrixGrabber 、 MatrixStack 、 MatrixTrackingGL: 这三个类就是为了实现一个功能、拦截当前的模型矩阵

Point: 平面上的点，主要是进行数学运算

Quadrilateral: 平面四边形类，进行点相对四边形的位置的判定

Render:Renderer 接口的实现类，负责图形渲染

SelfReduction: 魔方自动还原类，首先得到当前的魔方状态，然后进行一系列的计算与判断，最后算出还原的步骤

Settings: 游戏设置

Shape: 形状类， Cube 的父类

TimingCounter: 计时器、根据游戏的状态进行计时

Triangle: 三角形，判断一个点是在三角形内还是三角形外

Vertex: 顶点，每个立方体都有 8 个顶点

World: 游戏场景类，保存魔方顶点坐标、颜色、纹理坐标、索引数据

5.3 UI 设计

（ 1 ）主菜单：从图 5-1 中可以看到按钮有三种状态：正常状态、不可选状态、点击状态。根据按钮的状态。会自动选择按钮的背景图片、文字颜色。

编辑

添加图片注释，不超过 140 字（可选）

图5-1 主菜单界面

（ 2 ）游戏记录：在某条记录上长按会弹出删除对话框，如图 5-3 所示。游戏的排名是根据用时、用时相同根据步数、步数相同则根据日期 , 日期越新越靠前，如图 5-2 所示。

图5-2 游戏记录界面

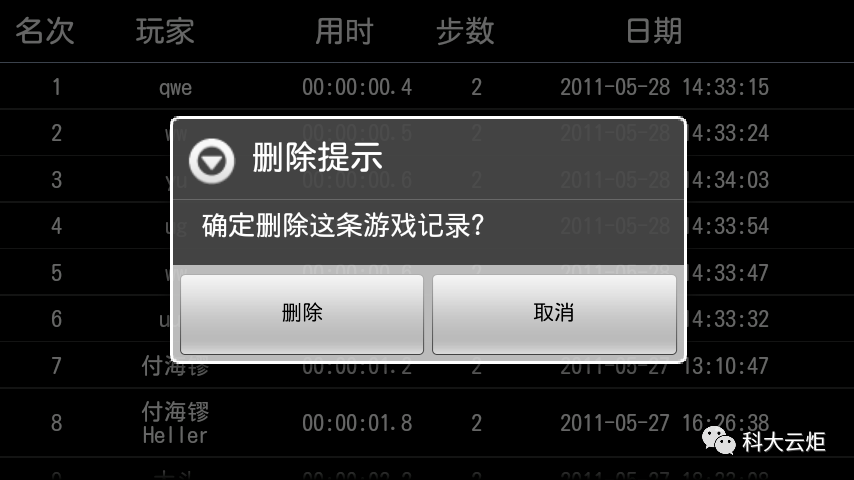
图5-3 删除游戏记录

（ 3 ）游戏说明：介绍游戏的操作及各个游戏菜单，如图 5-4 所示。

图5-4 游戏说明

（ 4 ）游戏界面：玩家可选择是否显示计时栏及控制按钮、可对魔方的大小进行调整。

图5-5 主游戏界面

（ 5 ）游戏成功界面：当玩家还原魔方成功的时候会提示保存游戏记录。如图5-6 所示

（ 6 ）游戏菜单：当按下键盘上的菜单键或屏幕上方的菜单按钮时、就会弹出如图 5-7 所示的游戏菜单

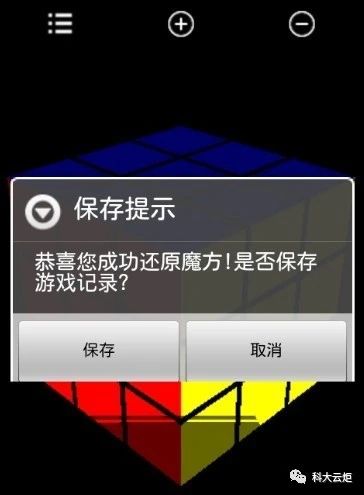
图5-7 游戏菜单

（ 7 ）游戏设置：可以对游戏的旋转速度、打乱步骤、计时栏状态等进行设置。

图5-8 游戏设置

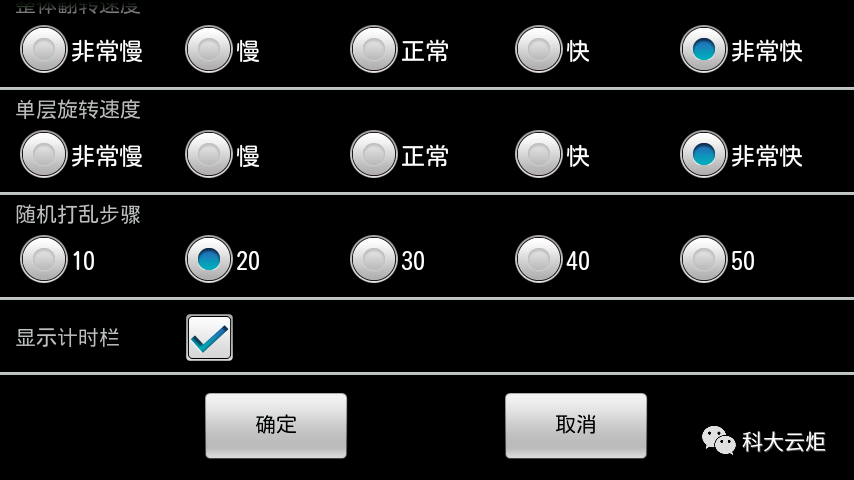
图5-9 游戏设置

（ 8 ）关于游戏 : 关于本游戏的一些信息，如版本、作者、版权等。如图 5-10所示。

图5-10 关于游戏

5.4功能设计

5.4.1 3D 魔方场景的构建

在 GameMain 类中调用 makeWorld 方法生成 27 个小立方体。对于每一个小立方体，它有八个顶点及六个面。 Cube 类继承于 Shape 类， Shape 类有一个 addVertex和 addFace 的方法， Cube 类继承了这两个方法，在生成每一个小立方的过程中，同时保存顶点和面及索引的数据，然后给魔方的每个面上色，最后通过 addShape方法将这 27 个小立方体添加到世界场景中，并创建魔方的 9 个层及分配每一层的小立方体，这时就得到了生成整个魔方所需要的所有数据。再通过 Render （渲染器）调用 World 类的 draw 方法进行图形的绘制。

5.4.2 魔方单个层的旋转

在 OpenGL ES 中，旋转这个操作的底层实现是通过维护一个 4*4 的矩阵来实现的。根据旋转轴的不同，生成不同的矩阵，然后将生成的矩阵与点的坐标相乘得到另一个坐标，该坐标即为旋转后的新坐标。

public void setAngle( float angle)

{

float twopi = ( float ) Math. PI * 2f ;

while (angle >= twopi)

angle -= twopi;

while (angle < 0f )

angle += twopi;

float sin = ( float ) Math.sin (angle);

float cos = ( float ) Math.cos (angle);

float [][] m = mTransform . matrix ;

switch ( mAxis )

{

case kAxisX :

m[1][1] = cos;

m[1][2] = sin;

m[2][1] = -sin;

m[2][2] = cos;

m[0][0] = 1f ;

m[0][1] = m[0][2] = m[1][0] = m[2][0] = 0f ;

break ;

case kAxisY :

m[0][0] = cos;

m[0][2] = sin;

m[2][0] = -sin;

m[2][2] = cos;

m[1][1] = 1f ;

m[0][1] = m[1][0] = m[1][2] = m[2][1] = 0f ;

break ;

case kAxisZ :

m[0][0] = cos;

m[0][1] = sin;

m[1][0] = -sin;

m[1][1] = cos;

m[2][2] = 1f ;

m[2][0] = m[2][1] = m[0][2] = m[1][2] = 0f ;

break ;

}

for ( int i = 0; i < mShapes . length ; i++)

{

Shape shape = mShapes [i];

if (shape != null )

shape.animateTransform( mTransform );

}

5.4.3 魔方整体的旋转

魔方的整体旋转可分解为三个层的同时旋转

5.4.4 OpenGL 3D 鼠标拾取的实现

（ 1 ） OpenGL 图形管线

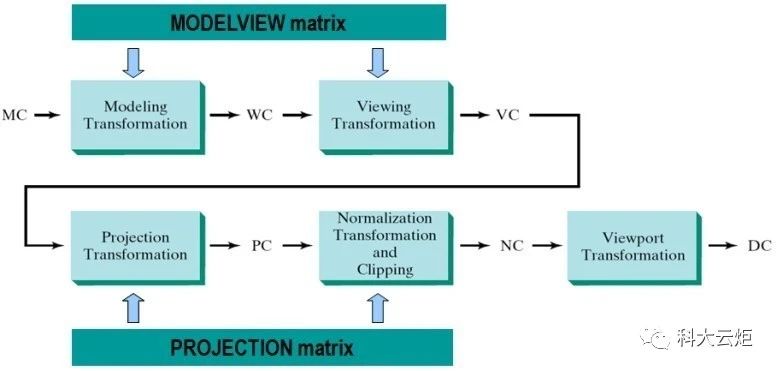
图5-11 OpenGL 图形管线

图 5-11 演示了 OpenGL 中关于坐标系统的一系列变换。在 OpenGL 中顶点坐标称作模型坐标。模型视图矩阵将这些坐标变换成视觉坐标。投影矩阵将视觉坐标变换成裁剪坐标。透视除法将裁剪坐标变换成规格化设备坐标。视口变换最终将这些坐标变换成窗口坐标。模型坐标，视觉坐标和裁剪坐标都为 4 维值，分别为 x,y,z和 w 坐标。因此，模型视图矩阵和物体矩阵为 4*4 矩阵 [13]。

（ 2 ）模型视图矩阵及投影矩阵的获取

在 OpenGL 中可以直接使用 glGetFloatv 这个方法获得 OpenGL 管线层的模型视图矩阵及投影矩阵 [14]。但在 OpenGL ES 中删除了这个方法，所以得自己手动拦截这两个矩阵。使用谷歌 ApiDemos 中的 MatrixGrabber 、 MatrixStack 、MatrixTrackingGL 这三个类就可以实现拦截。

（ 3 ）模型坐标与屏幕坐标的转换

拦截到模型视图矩阵与投影矩阵后，再加上一个视口坐标（通常就是屏幕的宽度和高度） , 根据上图的变换流程或使用系统提供的转换函数就能得到一个平面坐标 [15]。

GLU.gluProject(mVisibleVertexs[i].x, mVisibleVertexs[i].y, mVisibleVertexs[i].z, mMatrixGrabber.mModelView, 0, mMatrixGrabber.mProjection, 0, mRender.viewPort, 0, temp, 0);

在游戏视角下，玩家可见的魔方顶点一共有 37 个，通过 gluProject 方法可将这37 个三维坐标转换成 37 个平面坐标，这 37 个平面点又构成了 27 个不规则四边形，当玩家手指在屏幕上滑动的时候，会得到两个点（起点与终点）的平面坐标。根据起点所在区域决定魔方是进行整体的翻转还是单层的旋转。根据终点所在区域决定魔方的转动方向。

另外，因为 OpenGL 的坐标与 Windows 窗口的坐标不一样，所以进行判断之前还需要再进行一次坐标转换。 OpenGL 中的 (0,0) 点是在屏幕左下角，而 Windows的 (0,0) 点是在屏幕的左上角，所以 X 轴的坐标保持不变，但 Y 轴的坐标 y=height-y; height 是在渲染器的 onSurfaceChanged 中设定的，通常都会设定为屏幕的高度 [16]。

/* 当窗口大小发生改变时调用，在程序开始时至少运行一次，设置场景的大小 */

public void onSurfaceChanged(GL10 gl, int width, int height)

{

this . width = width;

this . height = height;

viewPort = new int [] { 0, 0, width, height };

float ratio = ( float ) width / height;

// 设置场景的大小

gl.glViewport(0, 0, width, height);

// 设置投影矩阵

gl.glMatrixMode(GL10. GL_PROJECTION );

// 重置投影矩阵

gl.glLoadIdentity();

// 设置视口的大小

gl.glFrustumf(-ratio, ratio, -1, 1, 2, 12);

// 得到投影矩阵

mGameMain . mMatrixGrabber .getCurrentProjection(gl);

// 选择模型观察矩阵

gl.glMatrixMode(GL10. GL_MODELVIEW );

// 重置当前模型观察矩阵

gl.glLoadIdentity();

}

（ 4 ）点与直线 (AB) 距离

// 点与直线 AB 的距离

public double getDistance(Point A, Point B)

{

// 分子

double numerator = Math.abs ((B. y - A. y ) * this . x + (A. x - B. x ) * this . y + B. x * A. y - A. x * B. y );

// 分母

double denominator = Math.sqrt ((A. x - B. x ) * (A. x - B. x ) + (A. y - B. y ) * (A. y - B. y ));

return numerator / denominator;

}

（ 5 ）两点之间的距离

// 两点之间的距离

public double getDistance(Point another)

{

return Math.sqrt (( x - another. x ) * ( x - another. x ) + ( y - another. y ) * ( y - another. y ));

}

（ 6 ）点与四边形的关系判断

连接点与四边形的四个点可得到四个角度，如果这 4 个角度相加为 360 度或者这 4 个角度中出现了 0 的情况，则点在四边形内或在四边形的边上。

/***********************************

******* A(p1) D(p4) *******

******* -------------- *******

******* \ O / *******

******* \ * / *******

******* \ / *******

******* ------ *******

******* B(p2) C(p3) *******

***********************************/

public boolean inQuadrilateral(Quadrilateral q)

{

double ab = q. p1 .getDistance(q. p2 );

double bc = q. p2 .getDistance(q. p3 );

double cd = q. p3 .getDistance(q. p4 );

double da = q. p4 .getDistance(q. p1 );

double oa = getDistance(q. p1 );

double ob = getDistance(q. p2 );

double oc = getDistance(q. p3 );

double od = getDistance(q. p4 );

double cosAOB = (oa * oa + ob * ob - ab * ab) / (2 * oa * ob);

double cosBOC = (ob * ob + oc * oc - bc * bc) / (2 * ob * oc);

double cosCOD = (oc * oc + od * od - cd * cd) / (2 * oc * od);

double cosDOA = (od * od + oa * oa - da * da) / (2 * oa * od);

double AOB = Math.acos (cosAOB);

double BOC = Math.acos (cosBOC);

double COD = Math.acos (cosCOD);

double DOA = Math.acos (cosDOA);

if (Math.abs (AOB + BOC + COD + DOA - Math. PI * 2) < exp )

return true ;

if (Math.abs (AOB) < exp || Math.abs (BOC) < exp || Math.abs(COD) < exp || Math.abs (DOA) < exp )

return true ;

return false ;

}

（ 7 ）点 (P) 与有向直线 (AB) 的关系判断（左边或右边或直线上）

PAB 组成一个三角形，利用三角形面积计算公式（如图 5-12 所示）：

编辑

添加图片注释，不超过 140 字（可选）

图5-12 三角形面积计算公式

这个表达式的正负数值，可以区分 P 位于 AB 直线的哪一侧。如果 s 是正的，表示三点逆时针排列，否则是顺时针排列，等于 0 是共线的。

编辑

添加图片注释，不超过 140 字（可选）

图5-13 点与直线的关系

// 判断点在有向直线（由点 A 与点 B 构成，方向为由 A 指向 B ）的哪一侧，返回 true表示在 AB 左侧，返回 false 表示 AB 在右侧

public boolean inLeftSide(Point A, Point B)

{

float a, b, c, d;

a = B. y - A. y ;

b = A. x - B. x ;

c = B. x * A. y - A. x * B. y ;

d = a * this . x + b * this . y + c;

// 小于 0 为左侧，大于 0 为右侧，等于 0 为在直线上

if (d < 0)

return true ;

else

return false ;

}

（ 8 ）点与三角形关系的判断

沿着三角形的顺时针或逆时针顺序，可依次得到三条有向直线，如果点都在这三条有向直线的同一侧，则在三角形中。

编辑

添加图片注释，不超过 140 字（可选）

图5-14 点与三角形关系

// 判断点是否在三角形内

public boolean inTriangle(Triangle mTriangle)

{

boolean b1 = this .inLeftSide(mTriangle. p1 , mTriangle. p2 );

boolean b2 = this .inLeftSide(mTriangle. p2 , mTriangle. p3 );

boolean b3 = this .inLeftSide(mTriangle. p3 , mTriangle. p1 );

if ((b1 && b2 && b3) || (!b1 && !b2 && !b3))

{

return true ;

}

else

return false ;

}

（ 9 ）翻转方向的确定

若触点在魔方区域外，则进行魔方的整体旋转。将游戏界面划分为 6 个区域，分别为左上、上、右上、左、右、左下、下、右下。对每一个区域进行如下判断：沿着每个区域作一条与魔方边缘平行的直线 AB （由 A 指向 B ），过该点（ A ）作直线（ AB ）的法线。这时候形成了一个垂直的十字架，共四个区域，然后分别作这四个区域的角平分线，形成了八个区域，如图 5-15 所示。然后根据点与有向直线的关系来判断手势终点所在的区域。

编辑切换为居中

添加图片注释，不超过 140 字（可选）

图5-15 触点区域判定

/**

* 点 A 和点 B 构成一条直线，当前点在直线 AB 外

* 过当前点作一条 AB 的法线，再作一条平行线

* 此时当前点与这两条新直线形成了四个区域

* 在每一个区域作一条角平分线，这时候就形成了八个区域

* 求 des 这个点在这八个区域中的哪一个，并返回区域号

* 求解过程：

* 根据直线 AB 和当前点，能算出平行线方程，在当前点右边取一点 P1 ，算出它的坐标

* 根据直线 AB 和当前点，能算出法线方程，在当前点上方取一点 P2 ，算出它的坐标

public int getAreaID(Point A, Point B, Point des)

{

Point p1 = new Point( this . x + 1, (A. y - B. y ) / (A. x - B. x ) + this . y );

Point p2 = new Point( this . x + 1, (B. x - A. x ) / (A. y - B. y ) + this . y );

// 0 、 1 、 2 、 3 区域

if (des.inLeftSide( this , p1))

{

// 0 、 1 区域

if (des.inLeftSide( this , p2))

{

// 区域 0

if (des.getDistance( this , p1) < des.getDistance( this, p2))

{

return 0;

}

// 区域 1

else

{

return 1;

}

// 2 、 3 区域

else

{

// 区域 3

if (des.getDistance( this , p1) < des.getDistance( this, p2))

{

return 3;

}

// 区域 2

else

{

return 2;

}

// 4 、 5 、 6 、 7 区域

else

{

// 6 、 7 区域

if (des.inLeftSide( this , p2))

{

// 区域 7

if (des.getDistance( this , p1) < des.getDistance( this, p2))

{

return 7;

}

// 区域 6

else

{

return 6;

}

// 4 、 5 区域

else

{

// 区域 4

if (des.getDistance( this , p1) < des.getDistance( this, p2))

{

return 4;

}

// 区域 5

else

{

return 5;

}

（ 10 ）旋转方向的确定

若起点在魔方区域内，则进行魔方的单层旋转，主要的情况如图 5-16 所示：

编辑

添加图片注释，不超过 140 字（可选）

图5-16 魔方单层旋转方向的判定

a . 终点在魔方上，而且与起点处于同一个四边形内

将起点与四边形的四个点连接起来，形成四个小三角形，然后判断终点落在哪个三角形内，点与三角形关系的判断前文已经提及。

编辑

添加图片注释，不超过 140 字（可选）

图5-17 起点与终点在同一个四边形内

b . 终点在魔方上，而且与起点处于同一个层

因为处于同一个层，所以层号可以确定，但仍需判断起点与终点的顺序，从而确定旋转的方向。

c . 终点在魔方上，但与起点不处于同一个四边形而且也不处于同一个层。判断方法与情况 d 一样。

d . 终点在魔方外

将起点所在四边形的四条边延伸出去，然后在四个角区域作角平分线，形成图5-18 所示情形。然后判断终点在哪一个区域。判断方法就是根据点与有向直线的关系。如果终点落在四个角区域，则需要再多加一次判断点是位于角平分线的哪一侧，根据点与直线的距离即可得到结果。

编辑切换为居中

添加图片注释，不超过 140 字（可选）

图5-18 魔方转动方向的判定

5.4.5 游戏记录

Android 内置了一个 SQLite 数据库，提供了数据库的接口。当游戏成功完成时，记录下玩家的步数、用时、当前日期、让玩家输入姓名，然后保存到数据库中。

数据库字段： _id ， name ， time ， step ， date

记录的删除：在游戏记录界面里，其实不只五列，在排名的左边还有一个隐藏列，记录的就是 _id ，玩家长按记录时，通过 _id 这个主键在数据库查找对应的记录并删除。

5.4.6 游戏计时

Java 里面提供了 Timer 、 TimerTask 、 Handler 类。游戏的计时就是这三个类的运用。 Timer 每隔 0.1 秒就发送一个响应， TimerTask 收到响应后获得当前游戏的状态、并将状态信息保存到消息中，交由 Handler 来处理， Handler 接收到后根据游戏状态来进行相关操作（如正在游戏，则毫秒加 1 ，暂停游戏将不作任何处理）。

5.4.7 放大缩小

OpenGL 中提供了一个缩放函数 glScalef() ，放大与缩小只需要设置一个变量scale ，然后每次响应到按钮点击的时候给 scale 一个增量即可。

// 设置三方向的缩放系数

gl.glScalef( scale , scale , scale );

5.4.8 随机打乱

Java 提供了一个 Random 类，能够生成指定范围的伪随机整数和布尔值，从而确定魔方转动的层 ID 与方向。

5.4.9 自动还原

首先得到魔方的当前状态，记录下当前每个面的颜色数据，保存为一个二维数组。魔方的每次转动都会改变这个数组，所以需要定义 18 个转换函数，分别对应魔方 6 个层（中间三个层除外）的顺、逆时针旋转及魔方整体旋转（ X 、 Y 、 Z的顺、逆时针翻转）的 6 种情况。每进行一次旋转，对新的状态进行判断，得到下一步的还原步骤。具体的还原方法为层先法。

5.4.10 游戏设置

当玩家按下“游戏设置”菜单时，首先得到当前的设置数据，并封装在一个intent 中，然后启动游戏设置的 Activity ，同时要求返回一个结果集（startActivityForResult ）。在游戏设置的 Activity 中，接收来自主游戏界面传递过来的设置数据，对单选及复选控件进行初始化，最后玩家点击确定按钮的时候，得到玩家的新设置信息，然后返回给主游戏界面的 Activity ，如果点击的是“取消”按钮。则将主游戏界面传递过来的设置信息原封不动地返回。

5.4.11 游戏成功判定

当玩家进行了层转动的操作后，对魔方的 Front 、 Right 、 Top 这三个面的颜色进行检测，如果这三个面的每一个面的颜色都相同，则可确定还原成功。

在游戏的过程中，玩家每转动（包括整体翻转与单层旋转）一次魔方，小立方体的朝向将会改变。在游戏刚开始时，魔方处于规则状态，每个面的朝向也是规律的，给每个小立方体的每个面增加一个索引值，当每转动一次魔方时，更新相关小立方体的面索引。举例：当玩家由左向右旋转了魔方的 Top 层，对于 Top 层的九个小立方体，它们原来的 Front 面变成了 Right 面， Right 面变成了 Back 面， Back面变成了 Left 面。 Left 面变成了 Front 面。

算法思路：首先得到旋转层的 9 个小立方体，根据旋转的方向可以得到一个转换序列 T ，如 Front 、 Right 、 Back 、 Left 。对于每一个小立方体，都有一个面数组，遍历这 6 个面，从序列 T 中查找当前面索引是否存在于 T 中，若存在，则将 T中的下一个值赋于当前面的索引变量。

public void updateFaceIndices( int k1, int k2, int k3, int k4)

{

int i = 0;

int j = 0;

int k = 0;

int [] src = new int [6];

int [] des = new int [6];

int [] transform = new int [] { k1, k2, k3, k4 };

Iterator<Face> iter1 = mFaceList .iterator();

while (iter1.hasNext())

{

src[i++] = iter1.next(). index ;

}

for (i = 0; i < src. length ; i++)

{

boolean NotFound = true ;

for (k = 0; k < transform. length ; k++)

{

if (src[i] == transform[k])

{

NotFound = false ;

if (k == 3)

des[j++] = transform[0];

else

des[j++] = transform[k + 1];

break ;

}

if (NotFound)

des[j++] = src[i];

}

i = 0;

Iterator<Face> iter2 = mFaceList .iterator();

while (iter2.hasNext())

{

iter2.next(). index = des[i++];

}

6 游戏测试

（1）在真机上测试时，发现当手机屏幕的方向改变，魔方也会自动改变，而且会重新调用 OnCreate 方法相当于重新开始游戏。解决方法：设定为游戏的布局为为某一固定方向即可。

（2）游戏计时：当重新开始游戏时、发现计时的速度加快，再重新开始，速度又再次加快。原因：游戏开始时会启动一个单独的线程来进行计时、点击“重新开始”按钮会又生成了一个线程，两个线程同时发出响应，所以速度越来越快。解决方法：在 Activity 的 onCreate 方法中生成计时对象，在onDestroy 方法中销毁计时对象。在 onResume 方法中启动计时。

（3）整体翻转时的万向节死锁问题。当魔方绕某一个轴翻转时，假设为 X 轴并向右上方翻转，则翻转完毕后模型坐标系的 Y 轴与 Z 轴同时也发生了改变。所以再次点翻转按钮的时候发现和预想中的完全不一样。解决方法：系统的 glRotatef 方法虽然能完成旋转的功能，但是同时也改变了模型视图矩阵，也加重了坐标转换的计算量，所以通过自己维护一个旋转矩阵来实现旋转的功能，而又不改变坐标轴的方向。

（4）放大与缩小：当魔方缩小到一定程度时突然就消失，而且再点击放大按钮都无任何反应。原因： scale 的值自减到了负数。解决方法：给 scale 设定一个下限。

（5）游戏状态的判断错误：当玩家返回到主菜单并再次切换游戏界面的时候游戏状态应该与之前的相同，但在日志里发现状态和想像中的不一致。原因：当 Activity 调用 onPause 方法的时候将魔方的状态设置为暂停，但返回时候得不到之前魔方的状态值。解决方法：设置一个临时的状态变量，当暂停的时候将当前游戏状态赋值给临时变量，返回的时候从临时状态变量中得到之前的状态。

（6）游戏步数的计算出错：原因，玩家成功还原魔方后，没有将步数重置为 0，所以出现了累加的现象。解决方法：游戏成功后置 0

（7）游戏排名出错：举例：玩家 A 用时 0.0.12 .9 ，玩家 B 用时 0.0.8.6 。结果 A排名靠前。原因：游戏的排名是根据用时来判断的，用时在数据库中的数据类型为文本型，所以默认情况下是进行字符串的比较。字符串是按 ASCII码来进行比较的，所以会出现上述错误。解决方法，当用时的每一部分不足两位数时，加一个前导 0. 同理，步数也是文本型，也会出现相同的情况，所以重新设置步数的字段为整形。

（8）当魔方正在随机打乱时，如果按下旋转按钮或重新开始菜单，出现整个魔方的变形，如图 5-19 所示。同样在魔方整体旋转时，如果又检测到新的手势，造成前一次的旋转未结束，又开始了新的旋转。解决方法，设置一个布尔值来判断魔方是否正在旋转，直到旋转完成后再开始新的操作。