数学基础从高一开始3、集合的基本运算2

---

目录

数学基础从高一开始3、集合的基本运算2

补集

例2：

总结：

---

补集

这里补集的符号我打不出来，这里就截图给大家看了啊。

下图是补集的语言表达，图形表达以及符号表达方式：

例1：设U={x|x是小于9的正整数}，A={1,2,3}，B={3,4,5,6}，求看下图(补集符号打不出来)： 

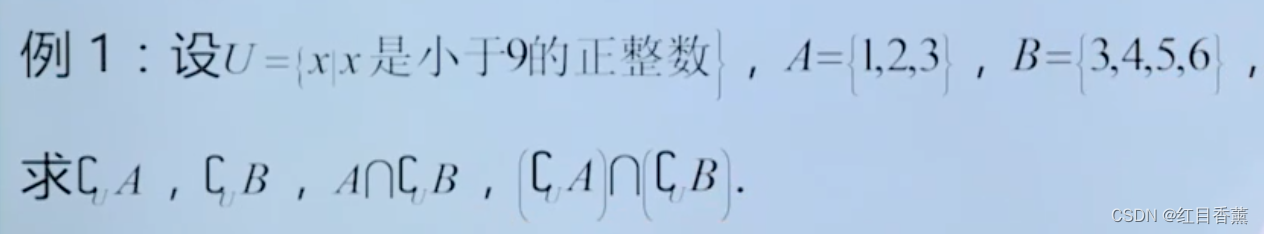
解：

由题意可知：U={1,2,3,4,5,6,7,8}，所有小于9的正整数。

集合A是{1,2,3}故而：补集uA={4,5,6,7,8}

集合B是{2,3,4,5}故而：补集uB={1,2,7,8}

集合A与补集uB他们两个都有的算式交集，故而=A∩补集uB{1,2}

交集就是都有，那么这里只有7和8，故而：(补集uA)∩(补集uB)={7,8}

这里理解起来还是非常容易的，基本上看一眼也就清楚怎么回事了。

例2：

设全集U={x|x是三角形}，A={x|x是锐角三角形}，B={x|x是钝角三角形}，求A∩B，补集u(A∪B)。 

解：

A∩B=∅

AUB={x|x是锐角三角形或钝角三角形}

补集u(A∪B)={x|是直角三角形}。

总结：

补集的概念：

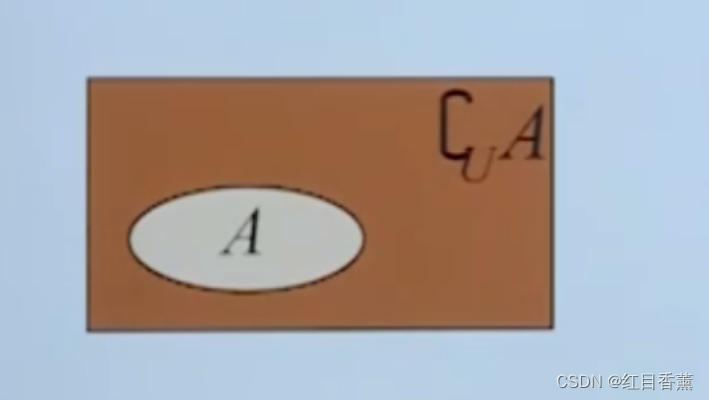
补集uA={x|x∈U，且x∉A}

方法反思：

连续数集可运用数轴增强直观性，抽象集合或关系较为复杂，可运用韦恩图的表示方法。