哈希表
首先什么是 哈希表,哈希表(英文名字为Hash table,国内也有一些算法书籍翻译为散列表,大家看到这两个名称知道都是指hash table就可以了)。
那么哈希表能解决什么问题呢,一般哈希表都是用来快速判断一个元素是否出现集合里。
哈希函数
如下图所示,通过hashCode把名字转化为数值,一般hashcode是通过特定编码方式,可以将其他数据格式转化为不同的数值,这样就把学生名字映射为哈希表上的索引数字了。
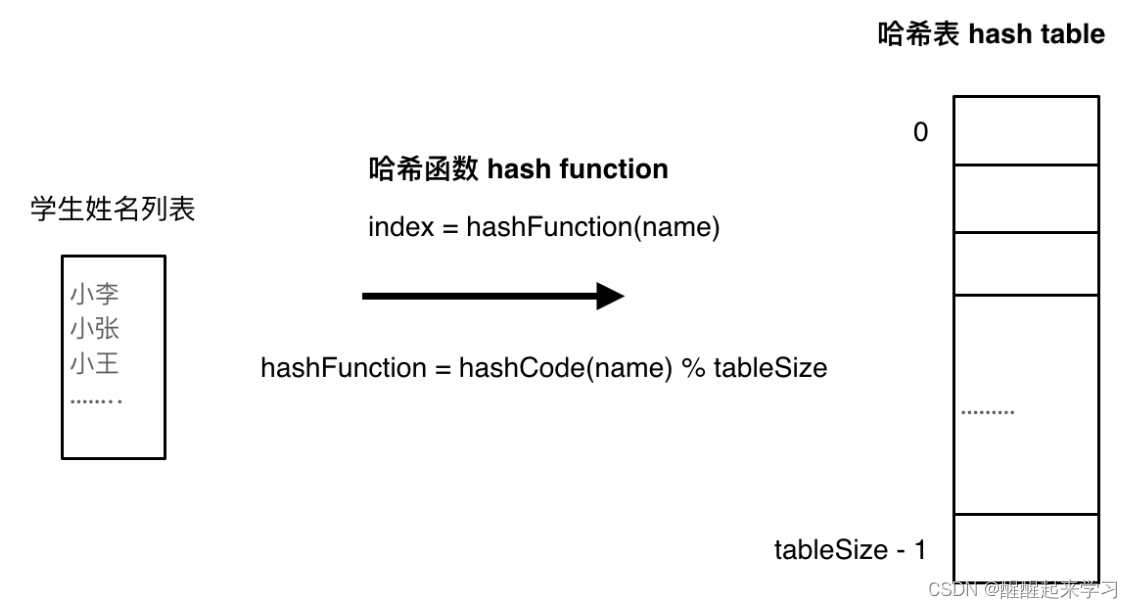
如果hashCode得到的数值大于 哈希表的大小了,也就是大于tableSize了,怎么办呢?
此时为了保证映射出来的索引数值都落在哈希表上,我们会在再次对数值做一个取模的操作,就要我们就保证了学生姓名一定可以映射到哈希表上了。
此时问题又来了,哈希表我们刚刚说过,就是一个数组。
如果学生的数量大于哈希表的大小怎么办,此时就算哈希函数计算的再均匀,也避免不了会有几位学生的名字同时映射到哈希表 同一个索引下标的位置。
接下来哈希碰撞登场
哈希碰撞
一般哈希碰撞有两种解决方法, 拉链法和线性探测法。
拉链法
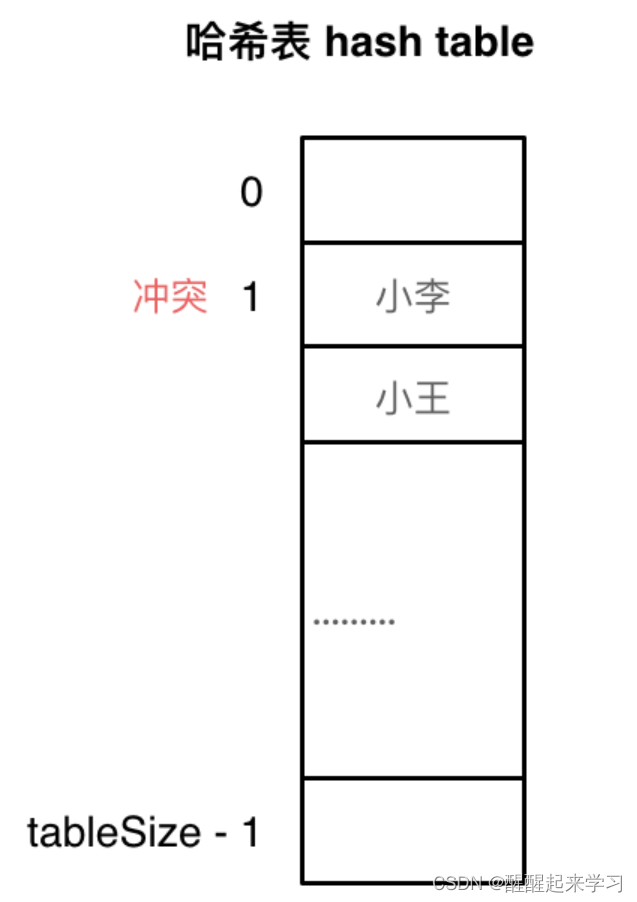
刚刚小李和小王在索引1的位置发生了冲突,发生冲突的元素都被存储在链表中。 这样我们就可以通过索引找到小李和小王了

(数据规模是dataSize, 哈希表的大小为tableSize)
其实拉链法就是要选择适当的哈希表的大小,这样既不会因为数组空值而浪费大量内存,也不会因为链表太长而在查找上浪费太多时间。
线性探测法
使用线性探测法,一定要保证tableSize大于dataSize。 因为我们需要依靠哈希表中的空位来解决碰撞问题。例如冲突的位置,放了小李,那么就向下找一个空位放置小王的信息。所以要求tableSize一定要大于dataSize ,要不然哈希表上就没有空置的位置来存放 冲突的数据了。如图所示:
常见的三种哈希结构
- 数组
- set (集合)
- map(映射)
242. 有效的字母异位词
思路:一开始利用hashmap一直做不出来,看了题解思路,自定义一个26位的数组arr,先将s的字符都在arr上标记(做加法),再将t的字符也在arr上标记(做减法),最后观察arr的变化
class Solution {
public boolean isAnagram(String s, String t) {
//将s放入hash表中,个数
//判断t中每一个字符在s中是否存在
int[] arr=new int[26];
for(int i=0;i<s.length();i++){
arr[s.charAt(i)-'a']++;//目的是使得相同字母能够定位到同一索引
}
for(int i=0;i<t.length();i++){
arr[t.charAt(i)-'a']--;//目的是使得相同字母能够定位到同一索引
}
for(int i=0;i<arr.length;i++){
if(arr[i]!=0){//如果是负数或者正数,则说明s和t肯定是不相同的
return false;
}
}
return true;
}
}349. 两个数组的交集
只会使用HashSet求解,看卡哥的解答是说用数组方式解答会更好,但是暂时没想到数组怎么做,
虽然代码AC了但是时间和空间复杂度都很低,垫底的存在,看了卡哥的思路跟我的思路是差不多的,但感觉哪里还能优化的呀。。
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
//使用set,或是使用数组
// 唯一元素
HashSet<Integer> set=new HashSet<Integer>();
HashSet<Integer> res=new HashSet<Integer>();
for(int i:nums1){
set.add(i);
}
for(int i:nums2){
if(set.contains(i)){
res.add(i);
}
}
return res.stream().mapToInt(Integer::intValue).toArray();
}
}学到了利用io流把集合转换成数组
下面是相同的方法:只是我对lambda表达式不熟练所以多看看写写
return res.stream().mapToInt(x -> x).toArray();
HashSet<Integer> set = new HashSet();
int[] a = set.stream().mapToInt(Integer::intValue).toArray()
202. 快乐数
这道题没有思路看的题解
数字n的最终结局分三种情况:
1.最终会得到 1。
2.最终会进入循环。
3.值会越来越大,最后接近无穷大。这种情况不可能存在解释如下:
情况3不可能存在,因为三位数999的下一位是81+81+81=243,9999的下一位是324
对于 3 位数的数字,它不可能大于 243。这意味着它要么被困在 243 以下的循环内,要么跌到 1。4 位或 4 位以上的数字在每一步都会丢失一位,直到降到 3 位为止。所以我们知道,最坏的情况下,算法可能会在 243 以下的所有数字上循环,然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去,所以我们排除第三种选择。
思路1-哈希法
个人理解
这道题目使用哈希法,来判断这个sum是否重复出现
这道题首先要获取下一个数,其次要判断这个数是否存在我们的集合中,如果存在,那么说明陷入循环了可以返回false,否则就一直重复获取下一个数
class Solution {
public boolean isHappy(int n) {
/**
1.最终会得到 1。
2.最终会进入循环。
3.值会越来越大,最后接近无穷大。这种情况不可能存在
*/
HashSet<Integer> set=new HashSet<Integer>();
//因为最多有 log n个数字会加入到set中
while(n!=1&&!set.contains(n)){//不包含这个数说明我们没有进入循环
set.add(n);
//不断更新n
n=getNext(n);
}
return n==1;
}
public int getNext(int n){
int res=0;
while(n>0){
int temp=n%10;
res+=temp*temp;
n/=10;
}
return res;
}
}思路2-双指针
通过反复调用 getNext(n) 得到的链是一个隐式的链表。如果n最终不会变成1,说明是这之间存在一个循环,如果存在循环的话,fast和slow指针二者最终是会相遇的
class Solution {
//快慢指针,如果n不可能变成1,那一定是一个循环,快慢指针终会相遇
public boolean isHappy(int n) {
/**
1.最终会得到 1。
2.最终会进入循环。
3.值会越来越大,最后接近无穷大。这种情况不可能存在
*/
int fast=getNext(n);//fast先走一步,同时出发报错
int slow=n;
//通过反复调用 getNext(n) 得到的链是一个隐式的链表。
// 两种结束循环的情况是:如果 n 是一个快乐数,即没有循环,那么快跑者最终会比慢跑者先到达数字 1。如果 n 不是一个快乐的数字,那么最终快跑者和慢跑者将在同一个数字上相遇。
while(fast!=1&&fast!=slow){
slow = getNext(slow);//走一步
fast = getNext(getNext(fast));//走两步
}
return fast==1;
}
public int getNext(int n){
int res=0;
while(n>0){
int temp=n%10;
res+=temp*temp;
n/=10;
}
return res;
}
}1.两数之和
半个月前做出来过,今天没做出来,尝试新思路也失败了,于是看了之前的提交记录
class Solution {
public int[] twoSum(int[] nums, int target) {
//两个for循环可以解决
//使用hashmap?
先把所有数字放到map中,
然后再遍历数组nums[i],
再在map中寻找target-nums[i],
注意要先把map中nums[i]对应的value-1,这个思路复杂,做不出来
//乖乖看题解
HashMap<Integer,Integer> map=new HashMap<Integer,Integer>();
for(int i=0;i<nums.length;i++){
if(map.containsKey(nums[i])){
return new int[]{i,map.get(nums[i])};//注意,这里是map.get(nums[i]
}
map.put(target-nums[i],i);//补数,索引
}
return new int[]{-1,-1};
}
}