文章目录
- 前言
- 一、Numpy概述
- 1.1 NumPy 简介
- 1.2 NumPy 安装
- 1.3 NumPy 操作
- 二、Ndarray 对象
- 2.1 概述
- 2.2 特点
- 2.3 Ndarray类
- 2.4 数据类型
- 三、Numpy 常用操作及函数
- 3.1 数组属性
- 3.2 创建数组
- 3.3 数组维度变换
- 3.4 ndarray数组的索引和切片
- 3.5 ndarray数组的运算
- 3.6 利用ndarray进行数据处理
- 1、NumPy的随机数函数
- 2、NumPy的统计类函数
- 3、NumPy的梯度函数
- 4、矩阵操作
- 3.7 广播机制
- 3.8 插值运算
- 3.9 曲线拟合
- 3.10 Numpy IO操作
- 四、结语
- 参考
前言
在上一篇中我们已经安装好基本环境。本期我们来学习Python中的一个强大核心库NumPy。
一、Numpy概述
1.1 NumPy 简介
NumPy(Numerical Python)是一个功能强大的 Python 库,支持多维数组与矩阵运算。它是Python数值计算最重要的基础包,大多数提供科学计算的包都是用NumPy的数组作为构建基础。NumPy本身并没有提供多么高级的数据分析功能,理解NumPy数组以及面向数组的计算,将有助于你更加高效地使用诸如Pandas之类的工具。
NumPy提供了大量的库函数和操作,可以帮助程序员轻松地进行数值计算。这类数值计算广泛用于机器学习模型、图像处理、数学任务等方面。
1.2 NumPy 安装
Anaconda默认已经安装了NumPy。如果未安装,可以按照以下命令进行安装。
pip install numpy
1.3 NumPy 操作
使用NumPy,开发人员可以执行以下操作:
- 数组的算数和逻辑运算。
- 傅立叶变换和用于图形操作的例程。
- 与线性代数有关的操作。 NumPy 拥有线性代数和随机数生成的内置函数。
二、Ndarray 对象
2.1 概述
NumPy 中定义的最重要的对象是称为 ndarray 的 N 维数组类型。 它是一系列相同类型数据的集合,以 0 下标为开始进行集合中元素的索引。
ndarray中的每个元素在内存中使用相同大小的块。 ndarray中的每个元素是数据类型对象的对象(称为 dtype)。
从ndarray对象提取的任何元素(通过切片)由一个数组标量类型的 Python 对象表示。 下图显示了ndarray,数据类型对象(dtype)和数组标量类型之间的关系。
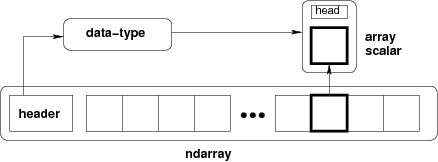
ndarray 内部由以下内容组成:
- 一个指向数据(内存或内存映射文件中的一块数据)的指针。
- 数据类型或 dtype,描述在数组中的固定大小值的格子。
- 一个表示数组形状(shape)的元组,表示各维度大小的元组。形状为(row×col)
2.2 特点
- ndarray 对象是用于存放同类型元素的多维数组。
- ndarray 中的每个元素在内存中都有相同存储大小的区域。
2.3 Ndarray类
ndarray类的实例可以通过本教程后面描述的不同的数组创建例程来构造。 基本的ndarray是使用 NumPy 中的数组函数创建的,如下所示:
numpy.array
它从任何暴露数组接口的对象,或从返回数组的任何方法创建一个ndarray。
numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0)
上面的构造器接受以下参数:
| 参数 | 参数及描述 |
|---|---|
object | 任何暴露数组接口方法的对象都会返回一个数组或任何(嵌套)序列。 |
dtype | 数组的所需数据类型,可选。 |
copy | 可选,默认为true,对象是否被复制。 |
order | C(按行)、F(按列)或A(任意,默认)读取数据并存储到内存中。 |
subok | 默认情况下,返回的数组被强制为基类数组。 如果为true,则返回子类。 |
ndmin | 指定返回数组的最小维数。 |
2.4 数据类型
numpy 支持的数据类型比 Python 内置的类型要多很多,基本上可以和C语言的数据类型对应上主要包括int8、int16、int32、int64、uint8、uint16、uint32、uint64、float16、float32、float64。
| 类型 | 解释 |
|---|---|
| bool | 布尔类型,1个字节,值为 True 或 False |
| int | 整数类型,通常为 int64 或 int32 |
| intc | 与 C 里的 int 相同,通常为 int32 或者 int64 |
| intp | 用于索引,通常为 int32 或者 int64 |
| int8 | 字节(从 -128 到 127) |
| int16 | 整数(从 -32768 到 32767) |
| int32 | 整数(从 -2147483648 到 2147483647) |
| int64 | 整数(从 -9223372036854775808 到 9223372036854775807) |
| uint8 | 无符号整数(从 0 到 255) |
| uint16 | 无符号整数(从 0 到 65535) |
| uint32 | 无符号整数(从 0 到 4294967295) |
| uint64 | 无符号整数(从 0 到 18446744073709551615) |
| float | float64的简写 |
| float16 | 半精度浮点,5 位指数,10 位尾数 |
| float32 | 半精度浮点,8 位指数,23 位尾数 |
| float64 | 半精度浮点,11 位指数,52 位尾数 |
| complex | complex128 的简写 |
| complex64 | 复数,由两个 32 为浮点表示 |
| complex128 | 复数,由两个 64 为浮点表示 |
三、Numpy 常用操作及函数
3.1 数组属性
| 属性 | 解释 |
|---|---|
| ndim | 秩,即数组的维数 |
| shape | 数组的维度大小(以元组形式) |
| size | 数组元素的个数 |
| itemsize | s数组元素的大小,以字节为单位 |
| dtype | 数组元素的数据类型 |
| astype | 类型转换 |
| T | 数组的转置(对高维数组而言) |
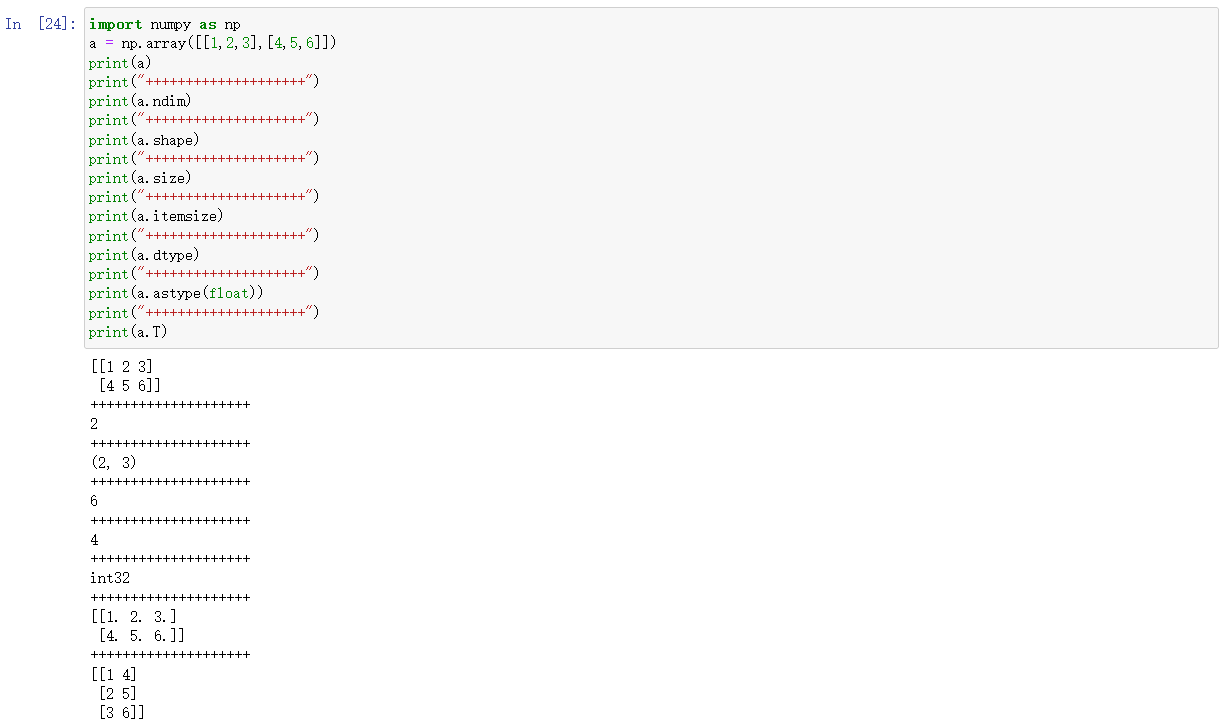
3.2 创建数组
| 方法 | 详解 |
|---|---|
| array() | 将列表转换为数组,可选择显式指定dtype |
| arange() | range的numpy版,支持浮点数 |
| linspace() | 类似arange(),第三个参数为数组长度 |
| zeros() | 根据指定形状和dtype创建全0数组 |
| ones() | 根据指定形状和dtype创建全1数组 |
| eye() | 创建单位矩阵 |
| empty() | 创建一个元素全随机的数组 |
| reshape() | 重塑形状 |
| full | 创建任意大小的数组并填充任意数字 |
3.3 数组维度变换
- .reshape(shape):不改变原数组元素,返回一个新的shape维度的数组**(维度变换)**
- .resize(shape):与.reshape()功能一致,但修改原数组**(维度变换)**
- .swapaxes(ax1,ax2) 将数组n个维度中两个维度进行调换**(维度变换)**
- .flatten():对数组进行降维,返回折叠后的一维数组,原数组不变**(维度变换)**
- .tolist():将N维数组转换成列表**(维度变换)**
3.4 ndarray数组的索引和切片
- 基本的索引和切片:基本索引与切片与python列表操作类似
a = np.array([[1,2,3],[4,5,6],[7,8,9]])
a[2]
#array(7,8,9)
a[0][2]
#3
a[:2,1:]
#array([[2,3],[5,6])
- 布尔索引:即根据布尔型数组进行数组索引,布尔型数组的长度必须与被索引的轴的长度一致
a = np.array([1,2,3,4,5])
c = np.array(['A','B','A','C','D'])
c == 'A'
#array([True,False,True,False,False])
a[char == 'A']
#array([1,3])
- 花式索引:指利用整数数组进行索引,为了以特定的顺序选取行子集,只需传入一个用于指定顺序的整数列表或ndarray即可
arr = np.empty((8,4))
for i in range(8):
arr[i]=i
arr
#array([[ 0., 0., 0., 0.],
[ 1., 1., 1., 1.],
[ 2., 2., 2., 2.],
...,
[ 5., 5., 5., 5.],
[ 6., 6., 6., 6.],
[ 7., 7., 7., 7.]])
arr[[4,3,0,6]]
#array([[ 4., 4., 4., 4.],
[ 3., 3., 3., 3.],
[ 0., 0., 0., 0.],
[ 6., 6., 6., 6.]])
3.5 ndarray数组的运算
- 数组与标量之间的运算,都会作用于数组的每一个元素;
- 大小相同的数组之间的任何算术运算,都会将运算应用到元素级;
- 大小相同的数组之间的比较运算,都会将运算应用到元素级并生成布尔值数组;
- np.abs(arr)\np.fabs(arr):计算数组arr各元素的绝对值
- np.sqrt(arr):计算数组arr各元素的平方根
- np.power(arr, n):计算数组arr各元素幂指数
- np.square(arr):计算数组arr各元素的平方
- np.log(arr)\np.log10(arr)\np.log2(arr):计算数组arr各元素的自然对数、10底对数和2底对数
- np.ceil(arr)\np.floor(arr):计算数组arr各元素的ceiling值 或 floor值
- np.rint(arr): 计算数组arr各元素的四舍五入值
- np.modf(arr): 将数组arr各元素的小数和整数部分以两个独立数组形式返回
- np.cos(arr)\np.cosh(arr)\np.sin(arr)\np.sinh(arr)\np.tan(arr)\np.tanh(arr):计算数组arr各元素的普通型和双曲型三角函数
- np.exp(arr): 计算数组arr各元素的指数值
- np.sign(arr): 计算数组arr各元素的符号值,1(+), 0, ‐1(‐)
- np.log(arr):计算数组arr各元素的对数
3.6 利用ndarray进行数据处理
1、NumPy的随机数函数
- np.random.rand(d0,d1,…,dn):根据d0‐dn创建随机数数组,浮点数,[0,1),均匀分布
- np.random.randn(d0,d1,…,dn):根据d0‐dn创建随机数数组,标准正态分布
- np.random.randint(low[,high,shape]):根据shape创建随机整数或整数数组,范围是[low, high)
- np.random.seed(s):随机数种子,s是给定的种
- np.random.shuffle(a):根据数组a的第1轴进行随排列,改变数组x
- np.random.permutation(a):根据数组a的第1轴产生一个新的乱序数组,不改变数组x
- np.random.choice(a[,size,replace,p]):从一维数组a中以概率p抽取元素,形成size形状新数组 replace表示是否可以重用元素,默认为False
- np.random.uniform(low,high,size):产生具有均匀分布的数组,low起始值,high结束值,size形状
- np.random.normal(loc,scale,size):产生具有正态分布的数组,loc均值,scale标准差,size形状
- np.random.poisson(lam,size):产生具有泊松分布的数组,lam随机事件发生率,size形状
2、NumPy的统计类函数
- np.sum(a, axis=None):根据给定轴axis计算数组a相关元素之和,axis整数或元组
- np.cumsum(a, axis=None):根据给定轴axis计算数组a相关元素之累计和,axis整数或元组
- np.mean(a, axis=None):根据给定轴axis计算数组a相关元素的期望,axis整数或元组
- np.average(a,axis=None,weights=None):根据给定轴axis计算数组a相关元素的加权平均值
- np.std(a, axis=None):根据给定轴axis计算数组a相关元素的标准差
- np.var(a, axis=None):根据给定轴axis计算数组a相关元素的方差
- np.min(a)\max(a):计算数组a中元素的最小值、最大值
- np.argmin(a)\argmax(a):计算数组a中元素最小值、最大值的降一维后下标
- np.unravel_index(index, shape):根据shape将一维下标index转换成多维下标
- np.ptp(a):计算数组a中元素最大值与最小值的差
- np.median(a):计算数组a中元素的中位数(中值)
3、NumPy的梯度函数
梯度:连续值之间的变化率,即斜率
XY坐标轴连续三个X坐标对应的Y轴值:a, b, c,其中,b的梯度是: (c‐a)/2
- np.gradient(f):计算数组f中元素的梯度,当f为多维时,返回每个维度梯度
4、矩阵操作
1、算术运算
算术运算指的是和标量之间的运算,ndarray 数组可以直接和标量进行各种算术运算,例如:+、-、*、/、%、//(整除)、**(次方)。
# 矩阵算术运算
n1 = np.random.randint(0,10,(2,3))
print(n1)
n2 = np.random.randint(0,10,(2,3))
print(n2)
n1 * n2
2、线性代数
线性代数中矩阵的操作主要包括:矩阵乘法、求逆矩阵、求矩阵的行列式、求矩阵的秩等。
| 函数 | 功能 |
|---|---|
| np.dot() | 矩阵乘法 |
| np.linalg.inv() | 求逆矩阵 |
| np.linalg.det() | 求矩阵的行列式 |
| np.linalg.matrix_rank() | 求矩阵的秩 |
下面是具体示例:
# 线性代数
n1 = np.random.randint(0,10,(2,3))
print(n1)
n2 = np.random.randint(0,10,(3,2))
print(n2)
print(np.dot(n1,n2)) #
n3 = np.random.randint(0,10,(2,2))
print(np.linalg.inv(n3)) # 求逆:Last 2 dimensions of the array must be square,数组的最后 2 个维度必须是正方形的
print(np.linalg.det(n3))
print(np.linalg.matrix_rank(n3))
3、其他数学操作
NumPy 中还有一些其他数学操作,具体可以参考:NumPy中文网。
3.7 广播机制
如果两个数组 a 和 b 形状相同,即满足 a.shape == b.shape ,那么算术运算可以对应元素进行;如果形状不同,NumPy会自动匹配广播机制,广播 (Broadcast) 是 numpy 对不同形状 (shape) 的数组进行数值计算的方式。
当运算中的 2 个数组的形状不同时,numpy 将自动触发广播机制。
1、广播的原则
- 如果两个数组的最后一个维度(trailing dimension,即
从末尾开始算起的维度)的维数相同,(在二维数组中表现为列数相同)。 - 两个数组行数相同,其中一方列维度为1,则认为它们是广播兼容的。广播会在缺失和(或)长度为1的维度上进行。
pandas 没有广播机制。
2、案例
# (1) 最后维度维数相同
n1 = np.array([
[1,4,3],
[9,1,5]
])
n2 = [
[3,6,1]
]
print(n1 + n2)
# (2) 其中一个维度为1
n3 = np.array([
[1],
[3]
])
n1 + n3
123456789101112131415
3.8 插值运算
这个过程其实就是我们在数学中已知一个函数,然后给出x值,让你根据这个函数求对应的y值,一般在曲线平滑处理中有较多的使用。
在Numpy中由 numpy.interp(x, xp, fp, left=None, right=None, period=None) 表示
- x - 表示将要计算的插值点x坐标
- xp - 表示已有的xp数组
- fp - 表示对应于已有的xp数组的值
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 2 * np.pi, 10)
y = np.sin(x)
xvals = np.linspace(0, 2 * np.pi, 10000)
yinterp = np.interp(xvals, x, y)
plt.plot(x, y, 'r-', xvals, yinterp, 'b-')
plt.show()
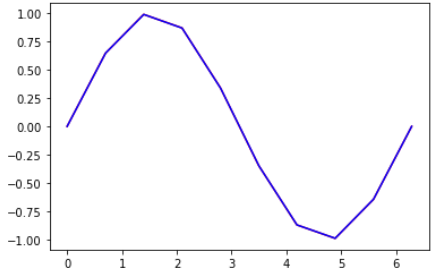
3.9 曲线拟合
我们在数学建模过程中得到我们的数据之后,如果我们想要使用某个函数去描述数据的规律,这个过程其实就在曲线拟合的过程,这里只介绍最简单的一种拟合方式。Numpy中由 numpy.polyfit(x, y, deg) 表示
- x为待拟合的x坐标
- y为待拟合的y坐标
- deg为拟合自由度,即多项式的最高次幂
import matplotlib.pyplot as plt
import numpy as np
x = np.array([0.0, 1.0, 2.0, 3.0, 4.0, 5.0])
y = np.array([0.0, 0.8, 0.9, 0.1, -0.8, -1.0])
#得到多项式的系数
z = np.polyfit(x, y, 3)
z2 = np.polyfit(x, y, 5)
#得到多项式函数
f = np.poly1d(z)
f2 = np.poly1d(z2)
#用两个函数进行拟合
xval = np.linspace(0, 10, 50)
yval1 = f(xval)
yval2 = f2(xval)
#作图
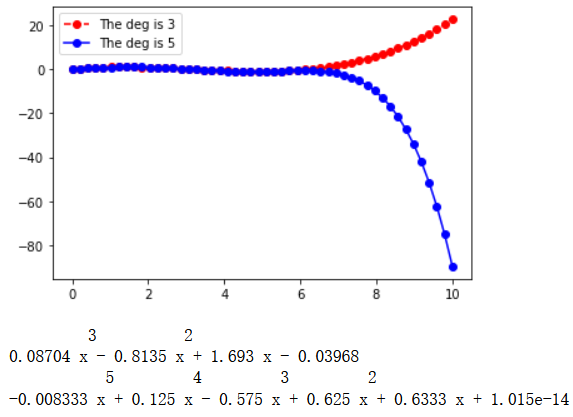
plt.plot(xval, yval1, 'r--o', xval, yval2, 'b-o')
plt.legend(['The deg is 3', 'The deg is 5'])
plt.show()
print(f) # out : 0.08704 x^3 - 0.8135 x^2 + 1.693 x - 0.03968
print(f2) # out : -0.008333 x^5 + 0.125 x^4 - 0.575 x^3 + 0.625 x^2 + 0.6333 x - 1.74e-14
3.10 Numpy IO操作
1、保存数组
保存一个数组到一个二进制的文件中,保存格式是.npy,Numpy中由np.save(file, array)表示。
2、读取文件
arr = numpy.load(file): 读取npy 文件到内存
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
#保存数据
np.save('test.npy', arr)
#下载数据
np.load('test.npy')
# out : array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
四、结语
本期跟大家分享的 “芝士” 就到此结束了,关于 NumPy 的基本操作,你学会了吗?
💕 好啦,这就是今天要分享给大家的全部内容了,我们下期再见! ✨
🍻 如果你喜欢的话,就不要吝惜你的一键三连了~ 🍻
如果文中有些地方不清楚的话,欢迎联系我,我会给大家提供思路及解答。
参考
Python Numpy库教程(超详细)
Python之numpy函数
Python之Numpy详细教程
Python NumPy用法
https://numpy.org/doc/stable/user/quickstart.html#indexing-slicing-and-iterating
https://seancheney.gitbook.io/python-for-data-analysis-2nd/di-04-zhang-numpy-ji-chu-shu-zu-he-shi-liang-ji-suan#ji-ben-de-suo-yin-he-qie-pian
numpy索引和切片
Python:numpy模块最详细的教程
python学习笔记之numpy库的使用——超详细
NumPy库的介绍与使用(一)