1.简述
1.无约束(无条件)的最优化
fminunc函数
: - 可用于任意函数求最小值
- 统一求最小值问题
- 如求最大值问题:
>对函数取相反数而变成求最小值问题,最后把函数值取反即为函数的最大值。
使用格式如下
1.必须预先把函数存入到一个程序中,(所编的程序一定是只有一个参数, 则当为多元函数时,则x(1),x(2),x(3)… 分别代表每个自变量);
2.fval 为函数的最小值,x0 为自变量初始向量,一般不影响结果(如有 n 个变量(即 n 元函数),则 x0 中就有 n 个元素);
3.exitflag 为退出标志,当它大于 0 时表示函数收敛于 x,当它等于 0 时表示迭代次数超过,当它小于 0 时表示函数不收敛(所以解完题后还必须判断 exitflag 的值是否>0,以决定结果的正误/有效性)
x=fminunc(‘程序名’, x0)
[x,fval]=fminunc()
[x,fval,exitflag]=fminunc()
函数可以用内联函数 inline(‘表达式’)
关于exitflag matlab帮助文档说明
1
Magnitude of gradient is smaller than the OptimalityTolerance tolerance.
2
Change in x was smaller than the StepTolerance tolerance.
3
Change in the objective function value was less than the FunctionTolerance tolerance.
5
Predicted decrease in the objective function was less than the FunctionTolerance tolerance.
0
Number of iterations exceeded MaxIterations or number of function evaluations exceeded MaxFunctionEvaluations.
-1
Algorithm was terminated by the output function.
-3
Objective function at current iteration went below ObjectiveLimit.
2.有约束条件的最优化
fminunc函数
(条件顺序:(线性)不等式—(线性)等式—上下限—非线性条件)
左边可为:
x=
[x,fval]=
[x,fval,exitflag]=
右边可为
(1) fmincon(‘程序名’,x0,A,b)
用于线性不等式约束, 即 Ax< =b,A 为系数矩阵,b 为常数项列向量,x0 为初始向量*
(2) fmincon(‘程序名’,x0,A,b,Aeq,beq)
用于线性不等式与线性等式约束,线性等式为 Aeq*x=beq, 其中 Aeq 为系数矩阵,为 beq 列向量
(3) fmincon(‘程序名’,x0, A,b,Aeq,beq, l,u)
其中 l、u 为解的上下限(即解的范围 l<=x<=u)
(如为多元函数:则 l=[x0,y0,z0,….], u=[xn,yn,zn,…])
(4)fmincon(‘程序名’,x0, A,b,Aeq,beq, l,u, ‘程序 2’)
其中 ‘程序 2’ 是用于非线性约束,它的格式为:c(x)<=0 ceq(x)=0
程序形式为:
function [c,ceq]=fu(x)
c=……;ceq=……;
1
2
注意:
1 如果不使用,必须使用空向量[ ]
2. 解完题后还必须判断 exitflag 的值是否>0,以决定结果的正误—所以最好返回三个结果,看一下 exitflag, 如无效则换一个初始向量 x0
2.代码
主程序:
%% 求解最大利润问题
x0=[0,0];
[xo_s,yo_s]=fminsearch('f1215',x0)
[xo_m,yo_m]=fminunc('f1215',x0)
子程序:
function [x,fval,exitflag,output] = fminsearch(funfcn,x,options,varargin)
%FMINSEARCH Multidimensional unconstrained nonlinear minimization (Nelder-Mead).
% X = FMINSEARCH(FUN,X0) starts at X0 and attempts to find a local minimizer
% X of the function FUN. FUN is a function handle. FUN accepts input X and
% returns a scalar function value F evaluated at X. X0 can be a scalar, vector
% or matrix.
%
% X = FMINSEARCH(FUN,X0,OPTIONS) minimizes with the default optimization
% parameters replaced by values in the structure OPTIONS, created
% with the OPTIMSET function. See OPTIMSET for details. FMINSEARCH uses
% these options: Display, TolX, TolFun, MaxFunEvals, MaxIter, FunValCheck,
% PlotFcns, and OutputFcn.
%
% X = FMINSEARCH(PROBLEM) finds the minimum for PROBLEM. PROBLEM is a
% structure with the function FUN in PROBLEM.objective, the start point
% in PROBLEM.x0, the options structure in PROBLEM.options, and solver
% name 'fminsearch' in PROBLEM.solver.
%
% [X,FVAL]= FMINSEARCH(...) returns the value of the objective function,
% described in FUN, at X.
%
% [X,FVAL,EXITFLAG] = FMINSEARCH(...) returns an EXITFLAG that describes
% the exit condition. Possible values of EXITFLAG and the corresponding
% exit conditions are
%
% 1 Maximum coordinate difference between current best point and other
% points in simplex is less than or equal to TolX, and corresponding
% difference in function values is less than or equal to TolFun.
% 0 Maximum number of function evaluations or iterations reached.
% -1 Algorithm terminated by the output function.
%
% [X,FVAL,EXITFLAG,OUTPUT] = FMINSEARCH(...) returns a structure
% OUTPUT with the number of iterations taken in OUTPUT.iterations, the
% number of function evaluations in OUTPUT.funcCount, the algorithm name
% in OUTPUT.algorithm, and the exit message in OUTPUT.message.
%
% Examples
% FUN can be specified using @:
% X = fminsearch(@sin,3)
% finds a minimum of the SIN function near 3.
% In this case, SIN is a function that returns a scalar function value
% SIN evaluated at X.
%
% FUN can be an anonymous function:
% X = fminsearch(@(x) norm(x),[1;2;3])
% returns a point near the minimizer [0;0;0].
%
% FUN can be a parameterized function. Use an anonymous function to
% capture the problem-dependent parameters:
% f = @(x,c) x(1).^2+c.*x(2).^2; % The parameterized function.
% c = 1.5; % The parameter.
% X = fminsearch(@(x) f(x,c),[0.3;1])
%
% FMINSEARCH uses the Nelder-Mead simplex (direct search) method.
%
% See also OPTIMSET, FMINBND, FUNCTION_HANDLE.
% Reference: Jeffrey C. Lagarias, James A. Reeds, Margaret H. Wright,
% Paul E. Wright, "Convergence Properties of the Nelder-Mead Simplex
% Method in Low Dimensions", SIAM Journal of Optimization, 9(1):
% p.112-147, 1998.
% Copyright 1984-2018 The MathWorks, Inc.
defaultopt = struct('Display','notify','MaxIter','200*numberOfVariables',...
'MaxFunEvals','200*numberOfVariables','TolX',1e-4,'TolFun',1e-4, ...
'FunValCheck','off','OutputFcn',[],'PlotFcns',[]);
% If just 'defaults' passed in, return the default options in X
if nargin == 1 && nargout <= 1 && strcmpi(funfcn,'defaults')
x = defaultopt;
return
end
if nargin < 3, options = []; end
% Detect problem structure input
if nargin == 1
if isa(funfcn,'struct')
[funfcn,x,options] = separateOptimStruct(funfcn);
else % Single input and non-structure
error('MATLAB:fminsearch:InputArg',...
getString(message('MATLAB:optimfun:fminsearch:InputArg')));
end
end
if nargin == 0
error('MATLAB:fminsearch:NotEnoughInputs',...
getString(message('MATLAB:optimfun:fminsearch:NotEnoughInputs')));
end
% Check for non-double inputs
if ~isa(x,'double')
error('MATLAB:fminsearch:NonDoubleInput',...
getString(message('MATLAB:optimfun:fminsearch:NonDoubleInput')));
end
n = numel(x);
numberOfVariables = n;
% Check that options is a struct
if ~isempty(options) && ~isa(options,'struct')
error('MATLAB:fminsearch:ArgNotStruct',...
getString(message('MATLAB:optimfun:commonMessages:ArgNotStruct', 3)));
end
printtype = optimget(options,'Display',defaultopt,'fast');
tolx = optimget(options,'TolX',defaultopt,'fast');
tolf = optimget(options,'TolFun',defaultopt,'fast');
maxfun = optimget(options,'MaxFunEvals',defaultopt,'fast');
maxiter = optimget(options,'MaxIter',defaultopt,'fast');
funValCheck = strcmp(optimget(options,'FunValCheck',defaultopt,'fast'),'on');
% In case the defaults were gathered from calling: optimset('fminsearch'):
if ischar(maxfun) || isstring(maxfun)
if strcmpi(maxfun,'200*numberofvariables')
maxfun = 200*numberOfVariables;
else
error('MATLAB:fminsearch:OptMaxFunEvalsNotInteger',...
getString(message('MATLAB:optimfun:fminsearch:OptMaxFunEvalsNotInteger')));
end
end
if ischar(maxiter) || isstring(maxiter)
if strcmpi(maxiter,'200*numberofvariables')
maxiter = 200*numberOfVariables;
else
error('MATLAB:fminsearch:OptMaxIterNotInteger',...
getString(message('MATLAB:optimfun:fminsearch:OptMaxIterNotInteger')));
end
end
switch printtype
case {'notify','notify-detailed'}
prnt = 1;
case {'none','off'}
prnt = 0;
case {'iter','iter-detailed'}
prnt = 3;
case {'final','final-detailed'}
prnt = 2;
case 'simplex'
prnt = 4;
otherwise
prnt = 1;
end
% Handle the output
outputfcn = optimget(options,'OutputFcn',defaultopt,'fast');
if isempty(outputfcn)
haveoutputfcn = false;
else
haveoutputfcn = true;
xOutputfcn = x; % Last x passed to outputfcn; has the input x's shape
% Parse OutputFcn which is needed to support cell array syntax for OutputFcn.
outputfcn = createCellArrayOfFunctions(outputfcn,'OutputFcn');
end
% Handle the plot
plotfcns = optimget(options,'PlotFcns',defaultopt,'fast');
if isempty(plotfcns)
haveplotfcn = false;
else
haveplotfcn = true;
xOutputfcn = x; % Last x passed to plotfcns; has the input x's shape
% Parse PlotFcns which is needed to support cell array syntax for PlotFcns.
plotfcns = createCellArrayOfFunctions(plotfcns,'PlotFcns');
end
header = ' Iteration Func-count min f(x) Procedure';
% Convert to function handle as needed.
funfcn = fcnchk(funfcn,length(varargin));
% Add a wrapper function to check for Inf/NaN/complex values
if funValCheck
% Add a wrapper function, CHECKFUN, to check for NaN/complex values without
% having to change the calls that look like this:
% f = funfcn(x,varargin{:});
% x is the first argument to CHECKFUN, then the user's function,
% then the elements of varargin. To accomplish this we need to add the
% user's function to the beginning of varargin, and change funfcn to be
% CHECKFUN.
varargin = [{funfcn}, varargin];
funfcn = @checkfun;
end
n = numel(x);
% Initialize parameters
rho = 1; chi = 2; psi = 0.5; sigma = 0.5;
onesn = ones(1,n);
two2np1 = 2:n+1;
one2n = 1:n;
% Set up a simplex near the initial guess.
xin = x(:); % Force xin to be a column vector
v = zeros(n,n+1); fv = zeros(1,n+1);
v(:,1) = xin; % Place input guess in the simplex! (credit L.Pfeffer at Stanford)
x(:) = xin; % Change x to the form expected by funfcn
fv(:,1) = funfcn(x,varargin{:});
func_evals = 1;
itercount = 0;
how = '';
% Initial simplex setup continues later
% Initialize the output and plot functions.
if haveoutputfcn || haveplotfcn
[xOutputfcn, optimValues, stop] = callOutputAndPlotFcns(outputfcn,plotfcns,v(:,1),xOutputfcn,'init',itercount, ...
func_evals, how, fv(:,1),varargin{:});
if stop
[x,fval,exitflag,output] = cleanUpInterrupt(xOutputfcn,optimValues);
if prnt > 0
disp(output.message)
end
return;
end
end
% Print out initial f(x) as 0th iteration
if prnt == 3
disp(' ')
disp(header)
fprintf(' %5.0f %5.0f %12.6g %s\n', itercount, func_evals, fv(1), how);
elseif prnt == 4
formatsave.format = get(0,'format');
formatsave.formatspacing = get(0,'formatspacing');
% reset format when done
oc1 = onCleanup(@()set(0,'format',formatsave.format));
oc2 = onCleanup(@()set(0,'formatspacing',formatsave.formatspacing));
format compact
format short e
disp(' ')
disp(how)
disp('v = ')
disp(v)
disp('fv = ')
disp(fv)
disp('func_evals = ')
disp(func_evals)
end
% OutputFcn and PlotFcns call
if haveoutputfcn || haveplotfcn
[xOutputfcn, optimValues, stop] = callOutputAndPlotFcns(outputfcn,plotfcns,v(:,1),xOutputfcn,'iter',itercount, ...
func_evals, how, fv(:,1),varargin{:});
if stop % Stop per user request.
[x,fval,exitflag,output] = cleanUpInterrupt(xOutputfcn,optimValues);
if prnt > 0
disp(output.message)
end
return;
end
end
% Continue setting up the initial simplex.
% Following improvement suggested by L.Pfeffer at Stanford
usual_delta = 0.05; % 5 percent deltas for non-zero terms
zero_term_delta = 0.00025; % Even smaller delta for zero elements of x
for j = 1:n
y = xin;
if y(j) ~= 0
y(j) = (1 + usual_delta)*y(j);
else
y(j) = zero_term_delta;
end
v(:,j+1) = y;
x(:) = y; f = funfcn(x,varargin{:});
fv(1,j+1) = f;
end
% sort so v(1,:) has the lowest function value
[fv,j] = sort(fv);
v = v(:,j);
how = 'initial simplex';
itercount = itercount + 1;
func_evals = n+1;
if prnt == 3
fprintf(' %5.0f %5.0f %12.6g %s\n', itercount, func_evals, fv(1), how)
elseif prnt == 4
disp(' ')
disp(how)
disp('v = ')
disp(v)
disp('fv = ')
disp(fv)
disp('func_evals = ')
disp(func_evals)
end
% OutputFcn and PlotFcns call
if haveoutputfcn || haveplotfcn
[xOutputfcn, optimValues, stop] = callOutputAndPlotFcns(outputfcn,plotfcns,v(:,1),xOutputfcn,'iter',itercount, ...
func_evals, how, fv(:,1),varargin{:});
if stop % Stop per user request.
[x,fval,exitflag,output] = cleanUpInterrupt(xOutputfcn,optimValues);
if prnt > 0
disp(output.message)
end
return;
end
end
exitflag = 1;
% Main algorithm: iterate until
% (a) the maximum coordinate difference between the current best point and the
% other points in the simplex is less than or equal to TolX. Specifically,
% until max(||v2-v1||,||v3-v1||,...,||v(n+1)-v1||) <= TolX,
% where ||.|| is the infinity-norm, and v1 holds the
% vertex with the current lowest value; AND
% (b) the corresponding difference in function values is less than or equal
% to TolFun. (Cannot use OR instead of AND.)
% The iteration stops if the maximum number of iterations or function evaluations
% are exceeded
while func_evals < maxfun && itercount < maxiter
if max(abs(fv(1)-fv(two2np1))) <= max(tolf,10*eps(fv(1))) && ...
max(max(abs(v(:,two2np1)-v(:,onesn)))) <= max(tolx,10*eps(max(v(:,1))))
break
end
% Compute the reflection point
% xbar = average of the n (NOT n+1) best points
xbar = sum(v(:,one2n), 2)/n;
xr = (1 + rho)*xbar - rho*v(:,end);
x(:) = xr; fxr = funfcn(x,varargin{:});
func_evals = func_evals+1;
if fxr < fv(:,1)
% Calculate the expansion point
xe = (1 + rho*chi)*xbar - rho*chi*v(:,end);
x(:) = xe; fxe = funfcn(x,varargin{:});
func_evals = func_evals+1;
if fxe < fxr
v(:,end) = xe;
fv(:,end) = fxe;
how = 'expand';
else
v(:,end) = xr;
fv(:,end) = fxr;
how = 'reflect';
end
else % fv(:,1) <= fxr
if fxr < fv(:,n)
v(:,end) = xr;
fv(:,end) = fxr;
how = 'reflect';
else % fxr >= fv(:,n)
% Perform contraction
if fxr < fv(:,end)
% Perform an outside contraction
xc = (1 + psi*rho)*xbar - psi*rho*v(:,end);
x(:) = xc; fxc = funfcn(x,varargin{:});
func_evals = func_evals+1;
if fxc <= fxr
v(:,end) = xc;
fv(:,end) = fxc;
how = 'contract outside';
else
% perform a shrink
how = 'shrink';
end
else
% Perform an inside contraction
xcc = (1-psi)*xbar + psi*v(:,end);
x(:) = xcc; fxcc = funfcn(x,varargin{:});
func_evals = func_evals+1;
if fxcc < fv(:,end)
v(:,end) = xcc;
fv(:,end) = fxcc;
how = 'contract inside';
else
% perform a shrink
how = 'shrink';
end
end
if strcmp(how,'shrink')
for j=two2np1
v(:,j)=v(:,1)+sigma*(v(:,j) - v(:,1));
x(:) = v(:,j); fv(:,j) = funfcn(x,varargin{:});
end
func_evals = func_evals + n;
end
end
end
[fv,j] = sort(fv);
v = v(:,j);
itercount = itercount + 1;
if prnt == 3
fprintf(' %5.0f %5.0f %12.6g %s\n', itercount, func_evals, fv(1), how)
elseif prnt == 4
disp(' ')
disp(how)
disp('v = ')
disp(v)
disp('fv = ')
disp(fv)
disp('func_evals = ')
disp(func_evals)
end
% OutputFcn and PlotFcns call
if haveoutputfcn || haveplotfcn
[xOutputfcn, optimValues, stop] = callOutputAndPlotFcns(outputfcn,plotfcns,v(:,1),xOutputfcn,'iter',itercount, ...
func_evals, how, fv(:,1),varargin{:});
if stop % Stop per user request.
[x,fval,exitflag,output] = cleanUpInterrupt(xOutputfcn,optimValues);
if prnt > 0
disp(output.message)
end
return;
end
end
end % while
x(:) = v(:,1);
fval = fv(:,1);
output.iterations = itercount;
output.funcCount = func_evals;
output.algorithm = 'Nelder-Mead simplex direct search';
% OutputFcn and PlotFcns call
if haveoutputfcn || haveplotfcn
callOutputAndPlotFcns(outputfcn,plotfcns,x,xOutputfcn,'done',itercount, func_evals, how, fval, varargin{:});
end
if func_evals >= maxfun
msg = getString(message('MATLAB:optimfun:fminsearch:ExitingMaxFunctionEvals', sprintf('%f',fval)));
if prnt > 0
disp(' ')
disp(msg)
end
exitflag = 0;
elseif itercount >= maxiter
msg = getString(message('MATLAB:optimfun:fminsearch:ExitingMaxIterations', sprintf('%f',fval)));
if prnt > 0
disp(' ')
disp(msg)
end
exitflag = 0;
else
msg = ...
getString(message('MATLAB:optimfun:fminsearch:OptimizationTerminatedXSatisfiesCriteria', ...
sprintf('%e',tolx), sprintf('%e',tolf)));
if prnt > 1
disp(' ')
disp(msg)
end
exitflag = 1;
end
output.message = msg;
%--------------------------------------------------------------------------
function [xOutputfcn, optimValues, stop] = callOutputAndPlotFcns(outputfcn,plotfcns,x,xOutputfcn,state,iter,...
numf,how,f,varargin)
% CALLOUTPUTANDPLOTFCNS assigns values to the struct OptimValues and then calls the
% outputfcn/plotfcns.
%
% state - can have the values 'init','iter', or 'done'.
% For the 'done' state we do not check the value of 'stop' because the
% optimization is already done.
optimValues.iteration = iter;
optimValues.funccount = numf;
optimValues.fval = f;
optimValues.procedure = how;
xOutputfcn(:) = x; % Set x to have user expected size
stop = false;
state = char(state);
% Call output functions
if ~isempty(outputfcn)
switch state
case {'iter','init'}
stop = callAllOptimOutputFcns(outputfcn,xOutputfcn,optimValues,state,varargin{:}) || stop;
case 'done'
callAllOptimOutputFcns(outputfcn,xOutputfcn,optimValues,state,varargin{:});
end
end
% Call plot functions
if ~isempty(plotfcns)
switch state
case {'iter','init'}
stop = callAllOptimPlotFcns(plotfcns,xOutputfcn,optimValues,state,varargin{:}) || stop;
case 'done'
callAllOptimPlotFcns(plotfcns,xOutputfcn,optimValues,state,varargin{:});
end
end
%--------------------------------------------------------------------------
function [x,FVAL,EXITFLAG,OUTPUT] = cleanUpInterrupt(xOutputfcn,optimValues)
% CLEANUPINTERRUPT updates or sets all the output arguments of FMINBND when the optimization
% is interrupted.
% Call plot function driver to finalize the plot function figure window. If
% no plot functions have been specified or the plot function figure no
% longer exists, this call just returns.
callAllOptimPlotFcns('cleanuponstopsignal');
x = xOutputfcn;
FVAL = optimValues.fval;
EXITFLAG = -1;
OUTPUT.iterations = optimValues.iteration;
OUTPUT.funcCount = optimValues.funccount;
OUTPUT.algorithm = 'Nelder-Mead simplex direct search';
OUTPUT.message = getString(message('MATLAB:optimfun:fminsearch:OptimizationTerminatedPrematurelyByUser'));
%--------------------------------------------------------------------------
function f = checkfun(x,userfcn,varargin)
% CHECKFUN checks for complex or NaN results from userfcn.
f = userfcn(x,varargin{:});
% Note: we do not check for Inf as FMINSEARCH handles it naturally.
if isnan(f)
error('MATLAB:fminsearch:checkfun:NaNFval',...
getString(message('MATLAB:optimfun:fminsearch:checkfun:NaNFval', localChar( userfcn ))));
elseif ~isreal(f)
error('MATLAB:fminsearch:checkfun:ComplexFval',...
getString(message('MATLAB:optimfun:fminsearch:checkfun:ComplexFval', localChar( userfcn ))));
end
%--------------------------------------------------------------------------
function strfcn = localChar(fcn)
% Convert the fcn to a character array for printing
if ischar(fcn)
strfcn = fcn;
elseif isstring(fcn) || isa(fcn,'inline')
strfcn = char(fcn);
elseif isa(fcn,'function_handle')
strfcn = func2str(fcn);
else
try
strfcn = char(fcn);
catch
strfcn = getString(message('MATLAB:optimfun:fminsearch:NameNotPrintable'));
end
end
子程序:
function [x,FVAL,EXITFLAG,OUTPUT,GRAD,HESSIAN] = fminunc(FUN,x,options,varargin)
%FMINUNC finds a local minimum of a function of several variables.
% X = FMINUNC(FUN,X0) starts at X0 and attempts to find a local minimizer
% X of the function FUN. FUN accepts input X and returns a scalar
% function value F evaluated at X. X0 can be a scalar, vector or matrix.
%
% X = FMINUNC(FUN,X0,OPTIONS) minimizes with the default optimization
% parameters replaced by values in OPTIONS, an argument created with the
% OPTIMOPTIONS function. See OPTIMOPTIONS for details. Use the
% SpecifyObjectiveGradient option to specify that FUN also returns a
% second output argument G that is the partial derivatives of the
% function df/dX, at the point X. Use the HessianFcn option to specify
% that FUN also returns a third output argument H that is the 2nd partial
% derivatives of the function (the Hessian) at the point X. The Hessian
% is only used by the trust-region algorithm.
%
% X = FMINUNC(PROBLEM) finds the minimum for PROBLEM. PROBLEM is a
% structure with the function FUN in PROBLEM.objective, the start point
% in PROBLEM.x0, the options structure in PROBLEM.options, and solver
% name 'fminunc' in PROBLEM.solver. Use this syntax to solve at the
% command line a problem exported from OPTIMTOOL.
%
% [X,FVAL] = FMINUNC(FUN,X0,...) returns the value of the objective
% function FUN at the solution X.
%
% [X,FVAL,EXITFLAG] = FMINUNC(FUN,X0,...) returns an EXITFLAG that
% describes the exit condition. Possible values of EXITFLAG and the
% corresponding exit conditions are listed below. See the documentation
% for a complete description.
%
% 1 Magnitude of gradient small enough.
% 2 Change in X too small.
% 3 Change in objective function too small.
% 5 Cannot decrease function along search direction.
% 0 Too many function evaluations or iterations.
% -1 Stopped by output/plot function.
% -3 Problem seems unbounded.
%
% [X,FVAL,EXITFLAG,OUTPUT] = FMINUNC(FUN,X0,...) returns a structure
% OUTPUT with the number of iterations taken in OUTPUT.iterations, the
% number of function evaluations in OUTPUT.funcCount, the algorithm used
% in OUTPUT.algorithm, the number of CG iterations (if used) in
% OUTPUT.cgiterations, the first-order optimality (if used) in
% OUTPUT.firstorderopt, and the exit message in OUTPUT.message.
%
% [X,FVAL,EXITFLAG,OUTPUT,GRAD] = FMINUNC(FUN,X0,...) returns the value
% of the gradient of FUN at the solution X.
%
% [X,FVAL,EXITFLAG,OUTPUT,GRAD,HESSIAN] = FMINUNC(FUN,X0,...) returns the
% value of the Hessian of the objective function FUN at the solution X.
%
% Examples
% FUN can be specified using @:
% X = fminunc(@myfun,2)
%
% where myfun is a MATLAB function such as:
%
% function F = myfun(x)
% F = sin(x) + 3;
%
% To minimize this function with the gradient provided, modify
% the function myfun so the gradient is the second output argument:
% function [f,g] = myfun(x)
% f = sin(x) + 3;
% g = cos(x);
% and indicate the gradient value is available by creating options with
% OPTIONS.SpecifyObjectiveGradient set to true (using OPTIMOPTIONS):
% options = optimoptions('fminunc','SpecifyObjectiveGradient',true);
% x = fminunc(@myfun,4,options);
%
% FUN can also be an anonymous function:
% x = fminunc(@(x) 5*x(1)^2 + x(2)^2,[5;1])
%
% If FUN is parameterized, you can use anonymous functions to capture the
% problem-dependent parameters. Suppose you want to minimize the
% objective given in the function myfun, which is parameterized by its
% second argument c. Here myfun is a MATLAB file function such as
%
% function [f,g] = myfun(x,c)
%
% f = c*x(1)^2 + 2*x(1)*x(2) + x(2)^2; % function
% g = [2*c*x(1) + 2*x(2) % gradient
% 2*x(1) + 2*x(2)];
%
% To optimize for a specific value of c, first assign the value to c.
% Then create a one-argument anonymous function that captures that value
% of c and calls myfun with two arguments. Finally, pass this anonymous
% function to FMINUNC:
%
% c = 3; % define parameter first
% options = optimoptions('fminunc','SpecifyObjectiveGradient',true); % indicate gradient is provided
% x = fminunc(@(x) myfun(x,c),[1;1],options)
%
% See also OPTIMOPTIONS, FMINSEARCH, FMINBND, FMINCON, @, INLINE.
% When options.Algorithm=='trust-region', the algorithm is a trust-region method.
% When options.Algorithm=='quasi-newton', the algorithm is the BFGS Quasi-Newton
% method with a mixed quadratic and cubic line search procedure.
% Copyright 1990-2018 The MathWorks, Inc.
% ------------Initialization----------------
defaultopt = struct( ...
'Algorithm', 'quasi-newton', ...
'DerivativeCheck','off', ...
'Diagnostics','off', ...
'DiffMaxChange',Inf, ...
'DiffMinChange',0, ...
'Display','final', ...
'FinDiffRelStep', [], ...
'FinDiffType','forward', ...
'ProblemdefOptions', struct, ...
'FunValCheck','off', ...
'GradObj','off', ...
'Hessian','off', ...
'HessMult',[], ...
'HessPattern','sparse(ones(numberOfVariables))', ...
'HessUpdate','bfgs', ...
'MaxFunEvals','100*numberOfVariables', ...
'MaxIter',400, ...
'MaxPCGIter','max(1,floor(numberOfVariables/2))', ...
'ObjectiveLimit', -1e20, ...
'OutputFcn',[], ...
'PlotFcns',[], ...
'PrecondBandWidth',0, ...
'TolFun',1e-6, ...
'TolFunValue',1e-6, ...
'TolPCG',0.1, ...
'TolX',1e-6, ...
'TypicalX','ones(numberOfVariables,1)', ...
'UseParallel',false ...
);
% If just 'defaults' passed in, return the default options in X
if nargin == 1 && nargout <= 1 && strcmpi(FUN,'defaults')
x = defaultopt;
return
end
if nargin < 3
options = [];
end
% Detect problem structure input
if nargin == 1
if isa(FUN,'struct')
[FUN,x,options] = separateOptimStruct(FUN);
else % Single input and non-structure.
error(message('optim:fminunc:InputArg'));
end
end
% No options passed. Set options directly to defaultopt after
allDefaultOpts = isempty(options);
% Prepare the options for the solver
options = prepareOptionsForSolver(options, 'fminunc');
% Set options to default if no options were passed.
if allDefaultOpts
% Options are all default
options = defaultopt;
end
% Check to see if the trust-region and large scale options conflict. If so,
% we'll error and ask the user to fix up the options.
if (isfield(options, 'Algorithm') && strcmp(options.Algorithm, 'trust-region')) && ...
(~isfield(options, 'GradObj') || strcmp(options.GradObj, 'off'))
[linkTag,endLinkTag] = linkToAlgDefaultChangeCsh('fminunc_error_trr_no_grad'); % links to context sensitive help
transitionMsgID = 'optim:fminunc:TrrOptionsConflict';
transitionMsgTxt = getString(message('optim:fminunc:TrrOptionsConflict',linkTag,endLinkTag));
error(transitionMsgID,transitionMsgTxt);
end
if nargin == 0
error(message('optim:fminunc:NotEnoughInputs'))
end
if nargout > 5
flags.computeHessian = true;
else
flags.computeHessian = false;
end
% Check for non-double inputs
msg = isoptimargdbl('FMINUNC', {'X0'}, x);
if ~isempty(msg)
error('optim:fminunc:NonDoubleInput',msg);
end
% Check for complex X0
if ~isreal(x)
error('optim:fminunc:ComplexX0', ...
getString(message('optimlib:commonMsgs:ComplexX0','Fminunc')));
end
XOUT=x(:);
sizes.nVar = length(XOUT);
sizes.mNonlinIneq = 0;
sizes.mNonlinEq = 0;
sizes.xShape = size(x);
medium = 'quasi-newton';
large = 'trust-region';
display = optimget(options,'Display',defaultopt,'fast',allDefaultOpts);
flags.detailedExitMsg = contains(display,'detailed');
switch display
case {'off','none'}
flags.verbosity = 0;
case {'notify','notify-detailed'}
flags.verbosity = 1;
case {'final','final-detailed'}
flags.verbosity = 2;
case {'iter','iter-detailed'}
flags.verbosity = 3;
case 'testing'
flags.verbosity = Inf;
otherwise
flags.verbosity = 2;
end
diagnostics = strcmpi(optimget(options,'Diagnostics',defaultopt,'fast',allDefaultOpts),'on');
% Check options needed for Derivative Check
options.GradObj = optimget(options,'GradObj',defaultopt,'fast',allDefaultOpts);
options.GradConstr = 'off';
options.DiffMinChange = optimget(options,'DiffMinChange',defaultopt,'fast',allDefaultOpts);
options.DiffMaxChange = optimget(options,'DiffMaxChange',defaultopt,'fast',allDefaultOpts);
% Read in and error check option TypicalX
[typicalx,ME] = getNumericOrStringFieldValue('TypicalX','ones(numberOfVariables,1)', ...
ones(sizes.nVar,1),'a numeric value',options,defaultopt);
if ~isempty(ME)
throw(ME)
end
checkoptionsize('TypicalX', size(typicalx), sizes.nVar);
options.TypicalX = typicalx;
options.FinDiffType = optimget(options,'FinDiffType',defaultopt,'fast',allDefaultOpts);
options = validateFinDiffRelStep(sizes.nVar,options,defaultopt);
options.UseParallel = optimget(options,'UseParallel',defaultopt,'fast',allDefaultOpts);
DerivativeCheck = strcmpi(optimget(options,'DerivativeCheck',defaultopt,'fast',allDefaultOpts),'on');
gradflag = strcmp(options.GradObj,'on');
Hessian = optimget(options,'Hessian',defaultopt,'fast',allDefaultOpts);
% line_search: 0 means trust-region, 1 means line-search ('quasi-newton')
line_search = strcmp(optimget(options,'Algorithm',defaultopt,'fast',allDefaultOpts), 'quasi-newton');
if ( strcmpi(Hessian,'on') || strcmpi(Hessian,'user-supplied') )
hessflag = true;
elseif strcmpi(Hessian,'off') || strcmpi(Hessian,'fin-diff-grads')
hessflag = false;
else
% If calling trust-region algorithm with an unavailable Hessian option value,
% issue informative error message
if ~line_search
error(message('optim:fminunc:BadTRReflectHessianValue'))
end
end
funValCheck = strcmp(optimget(options,'FunValCheck',defaultopt,'fast',allDefaultOpts),'on');
flags.computeLambda = 0;
% Convert to inline function as needed
if ~isempty(FUN) % will detect empty string, empty matrix, empty cell array
funfcn = optimfcnchk(FUN,'fminunc',length(varargin),funValCheck,gradflag,hessflag);
else
error(message('optim:fminunc:InvalidFUN'))
end
% For parallel finite difference (if needed) we need to send the function
% handles now to the workers. This avoids sending the function handles in
% every iteration of the solver. The output from 'setOptimFcnHandleOnWorkers'
% is a onCleanup object that will perform cleanup task on the workers.
UseParallel = optimget(options,'UseParallel',defaultopt,'fast',allDefaultOpts);
ProblemdefOptions = optimget(options, 'ProblemdefOptions',defaultopt,'fast',allDefaultOpts);
FromSolve = false;
if ~isempty(ProblemdefOptions) && isfield(ProblemdefOptions, 'FromSolve')
FromSolve = ProblemdefOptions.FromSolve;
end
cleanupObj = setOptimFcnHandleOnWorkers(UseParallel,funfcn,{''},FromSolve);
GRAD = zeros(sizes.nVar,1);
HESS = [];
switch funfcn{1}
case 'fun'
try
f = feval(funfcn{3},x,varargin{:});
catch userFcn_ME
optim_ME = MException('optim:fminunc:ObjectiveError', ...
getString(message('optim:fminunc:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
case 'fungrad'
try
[f,GRAD] = feval(funfcn{3},x,varargin{:});
catch userFcn_ME
optim_ME = MException('optim:fminunc:ObjectiveError', ...
getString(message('optim:fminunc:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
case 'fungradhess'
try
[f,GRAD,HESS] = feval(funfcn{3},x,varargin{:});
catch userFcn_ME
optim_ME = MException('optim:fminunc:ObjectiveError', ...
getString(message('optim:fminunc:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
case 'fun_then_grad'
try
f = feval(funfcn{3},x,varargin{:});
catch userFcn_ME
optim_ME = MException('optim:fminunc:ObjectiveError', ...
getString(message('optim:fminunc:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
try
GRAD = feval(funfcn{4},x,varargin{:});
catch userFcn_ME
optim_ME = MException('optim:fminunc:GradientError', ...
getString(message('optim:fminunc:GradientError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
case 'fun_then_grad_then_hess'
try
f = feval(funfcn{3},x,varargin{:});
catch userFcn_ME
optim_ME = MException('optim:fminunc:ObjectiveError', ...
getString(message('optim:fminunc:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
try
GRAD = feval(funfcn{4},x,varargin{:});
catch userFcn_ME
optim_ME = MException('optim:fminunc:GradientError', ...
getString(message('optim:fminunc:GradientError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
try
HESS = feval(funfcn{5},x,varargin{:});
catch userFcn_ME
optim_ME = MException('optim:fminunc:HessianError', ...
getString(message('optim:fminunc:HessianError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
otherwise
error(message('optim:fminunc:UndefCalltype'));
end
% Check for non-double data typed values returned by user functions
if ~isempty( isoptimargdbl('FMINUNC', {'f','GRAD','HESS'}, f, GRAD, HESS) )
error('optim:fminunc:NonDoubleFunVal',getString(message('optimlib:commonMsgs:NonDoubleFunVal','FMINUNC')));
end
% Check that the objective value is a scalar
if numel(f) ~= 1
error(message('optim:fminunc:NonScalarObj'))
end
% Check that the objective gradient is the right size
GRAD = GRAD(:);
if numel(GRAD) ~= sizes.nVar
error('optim:fminunc:InvalidSizeOfGradient', ...
getString(message('optimlib:commonMsgs:InvalidSizeOfGradient',sizes.nVar)));
end
% Determine algorithm
% If line-search and no hessian, then call line-search algorithm
if line_search && ...
(~strcmpi(funfcn{1}, 'fun_then_grad_then_hess') && ~strcmpi(funfcn{1}, 'fungradhess'))
output.algorithm = medium;
% Line-search and Hessian -- no can do, so do line-search after warning: ignoring hessian.
elseif line_search && ...
(strcmpi(funfcn{1}, 'fun_then_grad_then_hess') || strcmpi(funfcn{1}, 'fungradhess'))
warning(message('optim:fminunc:HessIgnored'))
if strcmpi(funfcn{1}, 'fun_then_grad_then_hess')
funfcn{1} = 'fun_then_grad';
elseif strcmpi(funfcn{1}, 'fungradhess')
funfcn{1} = 'fungrad';
end
output.algorithm = medium;
% If not line-search (trust-region) and Hessian, call trust-region
elseif ~line_search && ...
(strcmpi(funfcn{1}, 'fun_then_grad_then_hess') || strcmpi(funfcn{1}, 'fungradhess'))
l=[]; u=[]; Hstr=[];
output.algorithm = large;
% If not line search (trust-region) and no Hessian but grad, use sparse finite-differencing.
elseif ~line_search && ...
(strcmpi(funfcn{1}, 'fun_then_grad') || strcmpi(funfcn{1}, 'fungrad'))
n = length(XOUT);
Hstr = optimget(options,'HessPattern',defaultopt,'fast',allDefaultOpts);
if ischar(Hstr)
if strcmpi(Hstr,'sparse(ones(numberofvariables))')
% Put this code separate as it might generate OUT OF MEMORY error
Hstr = sparse(ones(n));
else
error(message('optim:fminunc:InvalidHessPattern'))
end
end
checkoptionsize('HessPattern', size(Hstr), n);
l=[]; u=[];
output.algorithm = large;
% Trust region but no grad, no can do; use line-search
elseif ~line_search
output.algorithm = medium;
else
error(message('optim:fminunc:InvalidProblem'))
end
% Set up confcn for diagnostics and derivative check
confcn = {''};
if diagnostics
% Do diagnostics on information so far
constflag = false; gradconstflag = false;
non_eq=0;non_ineq=0;lin_eq=0;lin_ineq=0;
diagnose('fminunc',output,gradflag,hessflag,constflag,gradconstflag,...
XOUT,non_eq,non_ineq,lin_eq,lin_ineq,[],[],funfcn,confcn);
end
% Create default structure of flags for finitedifferences:
% This structure will (temporarily) ignore some of the features that are
% algorithm-specific (e.g. scaling and fault-tolerance) and can be turned
% on later for the main algorithm.
finDiffFlags.fwdFinDiff = strcmpi(options.FinDiffType,'forward');
finDiffFlags.scaleObjConstr = false; % No scaling for now
finDiffFlags.chkFunEval = false; % No fault-tolerance yet
finDiffFlags.chkComplexObj = false; % No need to check for complex values
finDiffFlags.isGrad = true; % Scalar objective
finDiffFlags.hasLBs = false(sizes.nVar,1); % No lower bounds
finDiffFlags.hasUBs = false(sizes.nVar,1); % No lower bounds
% Check derivatives
if DerivativeCheck && gradflag % user wants to check derivatives
validateFirstDerivatives(funfcn,confcn,XOUT,-Inf(sizes.nVar,1), ...
Inf(sizes.nVar,1),options,finDiffFlags,sizes,varargin{:});
end
% Flag to determine whether to look up the exit msg.
flags.makeExitMsg = logical(flags.verbosity) || nargout > 3;
% If line-search and no hessian, then call line-search algorithm
if strcmpi(output.algorithm, medium)
[x,FVAL,GRAD,HESSIAN,EXITFLAG,OUTPUT] = fminusub(funfcn,x, ...
options,defaultopt,f,GRAD,sizes,flags,finDiffFlags,varargin{:});
elseif strcmpi(output.algorithm, large)
% Fminunc does not support output.constrviolation
computeConstrViolForOutput = false;
[x,FVAL,~,EXITFLAG,OUTPUT,GRAD,HESSIAN] = sfminbx(funfcn,x,l,u, ...
flags.verbosity,options,defaultopt,flags.computeLambda,f,GRAD,HESS,Hstr, ...
flags.detailedExitMsg,computeConstrViolForOutput,flags.makeExitMsg,varargin{:});
OUTPUT.algorithm = large; % override sfminbx output: not using the reflective
% part of the method
end
% Force a cleanup of the handle object. Sometimes, MATLAB may
% delay the cleanup but we want to be sure it is cleaned up.
delete(cleanupObj);
3.运行结果

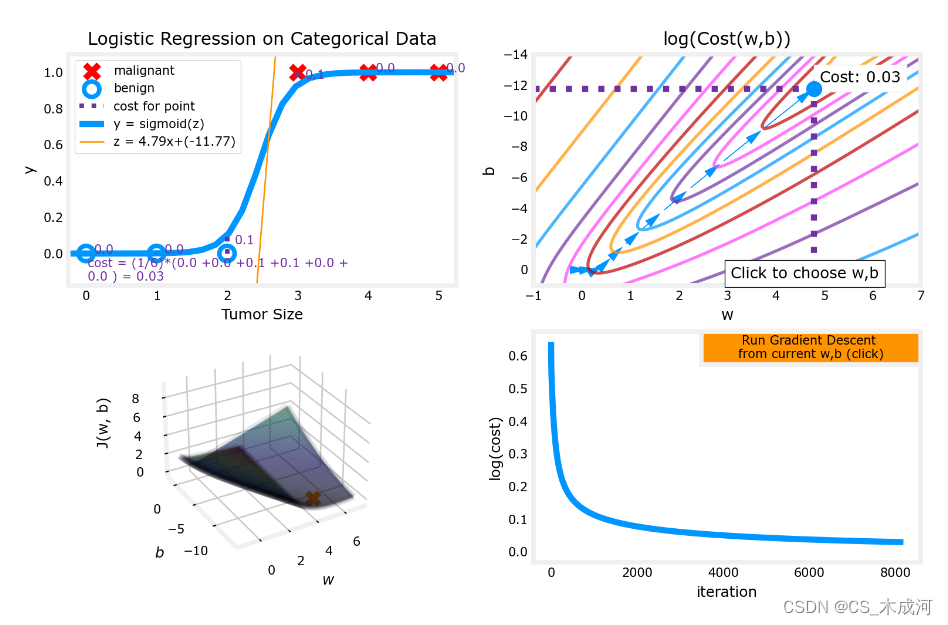



![[PAT乙级] 1029 旧键盘 C++实现](https://img-blog.csdnimg.cn/8a223f6ebe4e469b986313f2e5b8e3e8.png)