原题链接：https://codeforces.com/contest/1771/problem/B

题意 ：你总共有n个朋友编号1~n，其中m对互不认识，求1~n区间中没有互不认识的子段的总个数。

思路：总字段个数为每个编号前面的编号个数（包括自己）相加，为sum（1~n），例如，n为3时，编号1可以分成[1,1]、编号2可以分成[1,2]，[2,2]、编号3可以分成[1,3]，[2,3]，[3,3]。所有子段即为[1,1]，[1,2]，[2,2]，[1,3]，[2,3]，[3,3]，有6个。简而言之，就是3对应1和2和3，2对应1和2，1对应1这样分块。

既然知道了子段的分块方式，就能以这个为基础求没有互不认识的子段的总个数了。我们以将1~n的子段分成n块来看，第i块对应[1~i,i]的子段，每次取该子段之前不合法的右边界，第i块对方案的贡献数即为：i减去(1~i出现过的右边界的最大值）。

为什么是减去右边界的最大值呢？因为之前右边界不合法的数量被包含在更大的右边界里了

举一个简单的例子：

 该序列在2~3的时候右边界为1，在4的时候右边界为3，所以它在每块的方案数如下图

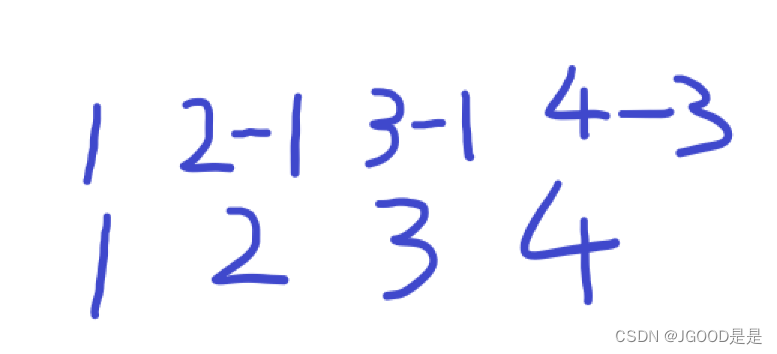
答案为1+1+2+1=5。有些同学可能会疑惑，为什么是减1和减3，而不是右边的减2和减4呢？这是因为我所说的右边界，是不能取到的区间子段数量的右边界，所以是减1和减3。例如编号3分块的子段是[1,3]，[2,3]，[3,3]，对于不合法的数{1,2}，{3,4}，其中只有[1,3]是不合法的，其它两个区间都是合法的。而[2,3]是合法的是因为{1,2}这数对没在区间[2,3]同时出现，{3,4}也是同样的道理。

编号4分块的子段是[1,4]，[2,4]，[3,4]，[4,4]，为什么它是减3而不是减1呢？因为前面的字段中，能包含{1,2}的子段一定也包含{3,4}，而包含{3,4}的子段却不一定包含{1,2}。所以要取右边界的最大值。对应的，对于数对{1,2}，在4分块中不能取的字段数量为1个,即右边界为1。对于数对{3,4},不能取的字段数量为3个，即右边界为3。

代码：

void solve() {
    map<int,int>mp;
    int n,m,ans=0;
    cin>>n>>m;
    FOR(1,m){
    	int x,y;
    	cin>>x>>y;
    	mp[max(x,y)]=max(mp[max(x,y)],min(x,y));
    }
    FOR(1,n){
    	mp[i]=max(mp[i],mp[i-1]);
    	ans+=i-mp[i];
    }
    cout<<ans<<endl;
}