第三章 栈和队列

3.1栈（stack）

3.1.1栈的基本概念

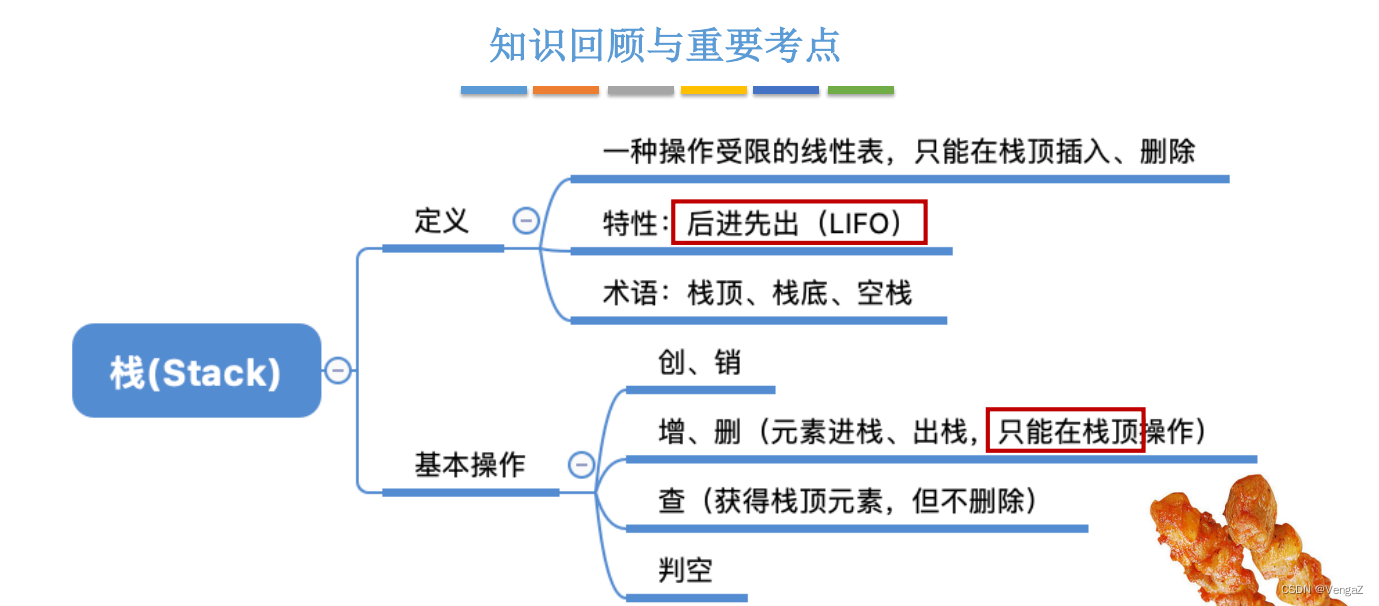
1. 栈的定义

• 栈是特殊的线性表：只允许在一端进行插入或删除操作， 其逻辑结构与普通线性表相同；
• 栈顶（Top）：允许进行插入和删除的一端 （最上面的为栈顶元素）；
• 栈底（Bottom）：固定的，不允许进行插入和删除的一端 （最下面的为栈底元素）；
• 空栈：不含任何元素的空表；

特点：LIFO 后进先出（后进栈的元素先出栈）可以实现特定的逻辑；
栈的增删改查操做的存取数据的时间复杂度均为O（1）

缺点：栈的大小不可变，解决方法——共享栈；
栈的数学性质： 卡特兰数
n个不同元素进栈，有$\frac{1}{n+1}{C}_{2n}^n$种不同的出栈书顺序

2. 栈的基本操作

“创建&销毁”

• InitStack(&S) 初始化栈：构造一个空栈S，分配内存空间；
• DestroyStack(&S) 销毁栈：销毁并释放栈S所占用的内存空间；

“增&删”

• Push(&S, x) 进栈：若栈S未满，则将x加入使其成为新栈顶；
• Pop(&S, &x) 出栈：若栈S非空，则弹出（删除）栈顶元素，并用x返回；

“查顶&判空”

• GetTop(S, &x) 读取栈顶元素：若栈S非空，则用x-返回栈顶元素；（栈的使用场景大多只访问栈顶元素）；
• StackEmpty(S) 判空： 断一个栈S是否为空，若S为空，则返回true,否则返回false；

---

栈的基本概念知识回顾

3.1.2 栈的顺序存储

1. 顺序栈的定义

#define MaxSize 10         //定义栈中元素的最大个数

typedef struct{
    ElemType data[MaxSize];       //静态数组存放栈中元素
    int top;                      //栈顶元素
}SqStack;

void testStack(){
    SqStack S;       //声明一个顺序栈(分配空间)
                     //连续的存储空间大小为 MaxSize*sizeof(ElemType)
}

注意此处的    int top;    //栈顶元素表示存储的是数组下标
其实用int * top用一个指针来实现逻辑也行

2. 顺序栈的基本操作

#define MaxSize 10         //定义栈中元素的最大个数

typedef struct{
    ElemType data[MaxSize];       //静态数组存放栈中元素
    int top;                      //栈顶元素
}SqStack;

分配的空间为 Maxsize*sizeof(ElemType),
但是是程序运行时系统分配的不是自己主动malloc的
所以不需要在最后free，所以只需要逻辑上回收将指针移动就行


//初始化栈
void InitStack(SqStack &S){
    S.top = -1;                   //初始化栈顶指针
}

//判栈空
bool StackEmpty(SqStack S){
    if(S.top == -1)      //栈空
        return true;
    else                 //栈不空
        return false;
}

//新元素进栈
bool Push(SqStack &S, ElemType x){
    if(S.top == MaxSize - 1)        //栈满
        return false;
    
    S.top = S.top + 1;    //指针先加1
    S.data[S.top] = x;    //新元素入栈

    /*
    S.data[++S.top] = x;
    */
    return true;
}

//出栈
bool Pop(SqStack &x, ElemType &x){
    if(S.top == -1)          //栈空
        return false;
    
    x = S.data[S.top];       //先出栈
    S.top = S.top - 1;       //栈顶指针减1
    return true;

    /*
    x = S.data[S.top--];
    */

    只是逻辑上的删除，数据依然残留在内存里
    但是这个程序执行结束，对应的内存系统会自行回收

}

//读栈顶元素
bool GetTop(SqStack S, ElemType &x){
    if(S.top == -1)
        return false;
    
    x = S.data[S.top];      //x记录栈顶元素
    return true; 
}


void testStack(){
    SqStack S;       //声明一个顺序栈(分配空间)
    InitStack(S);
    //...
}

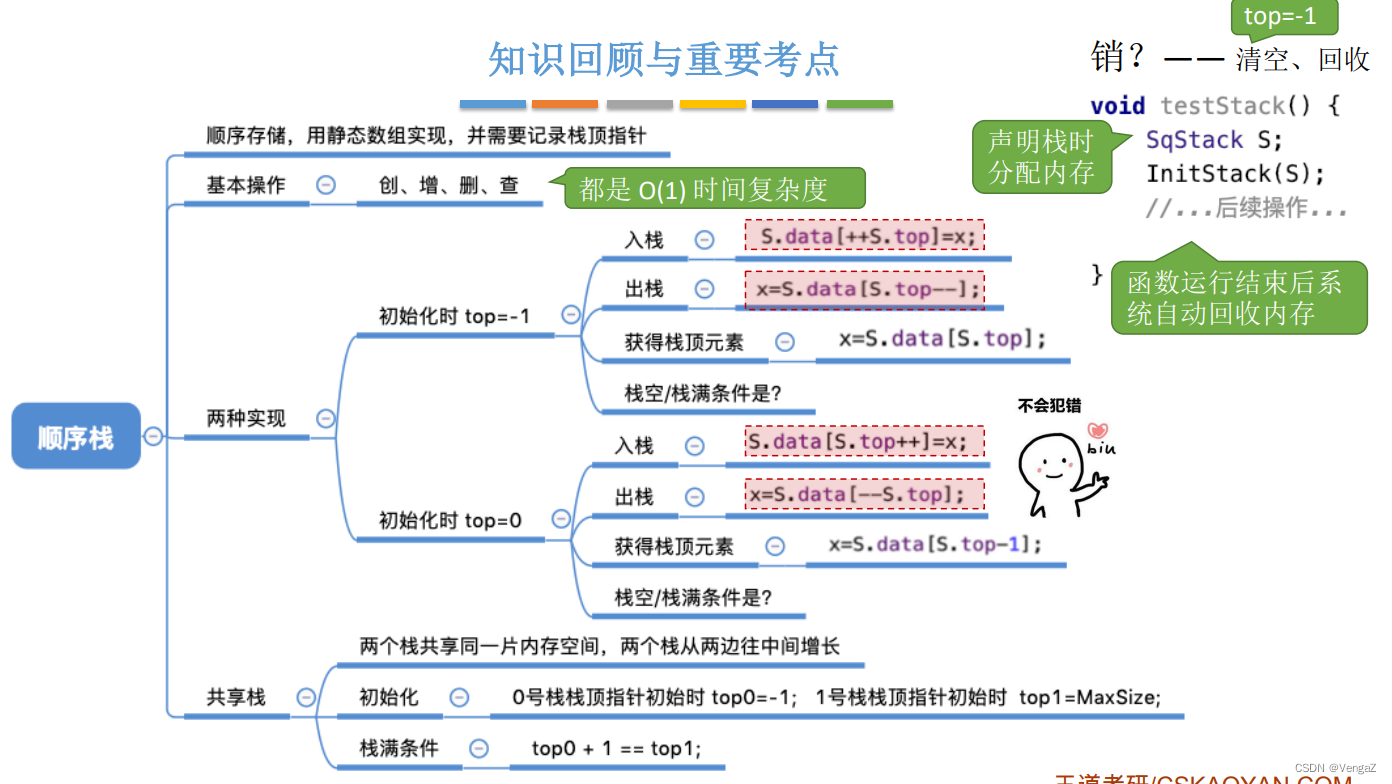
另一种设置栈顶指针位置的方法：初始化时定义 S.top = 0 ；top指针指向下一个可以插入元素的位置，也就是栈顶元素的后一个位置。
(总的来说，之前那种方法是top指针指向已经有元素的位置并且top == -1为判空条件，这种方法是指向没有元素的位置并且top == 0为判空条件)

初始化时定义 S.top = 0：

• 进栈操作 ：栈不满时，栈顶指针先加1，再送值到栈顶元素。S.data[S.top++] = x;
• 出栈操作：栈非空时，先取栈顶元素值，再将栈顶指针减1。`x = S.data[–S.top];
• 栈空条件：S.top==-1
• 栈满条件：S.top==MaxSize-1
• 栈长：S.top+1

3.共享栈
定义：利用栈底位置相对不变的特性，可以让两个顺序栈共享一个一维数组空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间的中间延伸。

---

#define MaxSize 10         //定义栈中元素的最大个数

typedef struct{
    ElemType data[MaxSize];       //静态数组存放栈中元素
    int top0;                     //0号栈栈顶指针
    int top1;                     //1号栈栈顶指针
}ShStack;

//初始化栈
void InitSqStack(ShStack &S){
    S.top0 = -1;        //初始化栈顶指针
    S.top1 = MaxSize;   
}
			共享栈 栈满条件：S.top0 + 1 = S.top

---

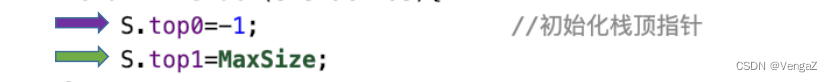
上溢与下溢

参考博客: 上溢与下溢

上溢与下溢分为堆栈的上溢与下溢和缓冲区的上溢和下溢

1. 堆栈的上溢与下溢

堆栈区域是在堆栈定义时就确定了的，因而堆栈工作过程中有可能产生溢出。堆栈溢出有两种情况可能发生：如堆栈已满，但还想再存入信息，这种情况称为堆栈上溢；另一种情况是，如堆栈已空，但还想再取出信息，这种情况称为堆栈下溢。

---

采取保护措施：这可以通过给SP规定上、下限，在进栈或出栈操作前先做SP和边界值的比较，如溢出则作溢出处理，以避免破坏其他存储区或使程序出错的情况发生。

共享栈只有在整个对堆栈空间被占满才发生上溢，因为栈是只在头部进行操作的一种抽象数据结构，所以只可能发生上溢

2. 缓冲区的上溢和下溢

上溢就是缓冲器满，还往里写；下溢就是缓冲器空，还往外读.
软件对硬件处理的不合理，速度的不一导致的上溢与下溢

---

如果指数据发送太快,硬件处理不过来,缓存已经装不下那么多数据,开始丢弃这些数据,放弃处理.这就是指上溢.
如果数据发送太慢,缓冲区的数据都处理空了,输入数据还没过来,硬件还在等待缓冲区有足够数据可以处理,输出接口就在要求发送处理好的数据出去,就是指下溢.

栈的顺序存储知识回顾

3.1.3栈的链式存储

1. 定义：采用链式存储的栈称为链栈，且多采用单链表来实现。
2. 优点：链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。
3. 特点：

进栈和出栈都只能在栈顶一端进行(链头作为栈顶)
链表的头部作为栈顶，意味着：（都是对链表的头进行操作）

• 在实现数据"入栈"操作时，需要将数据从链表的头部插入；
• 在实现数据"出栈"操作时，需要删除链表头部的首元节点；

因此，链栈实际上就是一个只能采用头插法插入或删除数据的链表;
栈的链式存储结构可描述为：

typedef struct Linknode{
    ElemType data;              //数据域
    struct Linknode *next;      //指针域
}*LiStack;                      //栈类型的定义

链栈的基本操作

• 初始化
• 进栈
• 出栈
• 获取栈顶元素
• 判空、判满

1. 带头结点的链栈基本操作：

#include<stdio.h>

struct Linknode{
    int data;             //数据域
    Linknode *next;       //指针域
}Linknode,*LiStack;   

typedef Linknode *Node;   //结点结构体指针变量
typedef Node List;        //结点结构体头指针变量

//1. 初始化
void InitStack(LiStack &L){   //L为头指针
    L = new Linknode; 
    L->next = NULL;
}

//2.判栈空
bool isEmpty(LiStack &L){
    if(L->next == NULL){
        return true;
    }
    else
        return false;
}

//3. 进栈(：链栈基本上不会出现栈满的情况)
void pushStack(LiStack &L, int x){
    Linknode s;          //创建存储新元素的结点
    s = new Linknode;
    s->data = x;

    //头插法
    s->next = L->next;
    L->next = s;
}

//4.出栈
bool popStack(LiStack &L, int &x){
    Linknode s;
    if(L->next == NULL) //栈空不能出栈
        return false;
    
    s = L->next;
    x = s->data;
    L->next = L->next->next;
    delete(s);

    return true;
}

2. 不带头结点的链栈基本操作：

#include<stdio.h>

struct Linknode{
    int data;             //数据域
    Linknode *next;       //指针域
}Linknode,*LiStack;   

typedef Linknode *Node;   //结点结构体指针变量
typedef Node List;        //结点结构体头指针变量

//1.初始化 
void initStack(LiStack &L){
    L=NULL;
}

//2.判栈空
bool isEmpty(LiStack &L){
    if(L == NULL)
        return true;
    else
        teturn false;
}

//3.进栈
void pushStack(LiStack &L, int x){
    Linknode s;          //创建存储新元素的结点
    s = new Linknode;

    s->next = L;
    L = s;
}

//4.出栈
bool popStack(LiStack &L, int &x){
    Linknode s; 
    if(L = NULL)     //栈空不出栈
        return false;

    s = L;
    x = s->data;
    L = L->next;
    delete(s);
    
    return true;
}

3.2队列（Queue）

3.2.1队列的基本概念

1. 定义：队列（Queue）简称队，是一种操作受限的线性表，只允许在表的一端进行插入，而在表的另一端进行删除。
2. 特点

• 队列是操作受限的线性表，只允许在一端进行插入 (入队)，另一端进行删除 (出队)
• 操作特性：先进先出 FIFO
• 队头：允许删除的一端
• 队尾：允许插入的一端
• 空队列：不含任何元素的空表

3. 队列的基本操作

• “创建&销毁”

InitQueue(&Q): 初始化队列，构造一个空列表Q
DestroyQueue(&Q): 销毁队列，并释放队列Q所占用的内存空间

• “增&删”

EnQueue(&Q, x): 入队，若队列Q未满，将x加入，使之成为新的队尾
DeQueue(&Q, &x): 出队，若队列Q非空，删除队头元素，并用x返回

• “查&其他”

GetHead(Q,&x): 读队头元素，若队列Q非空，则将队头元素赋值给x
QueueEmpty(Q): 判队列空，若队列Q为空，则返回

3.2.2队列的顺序存储结构

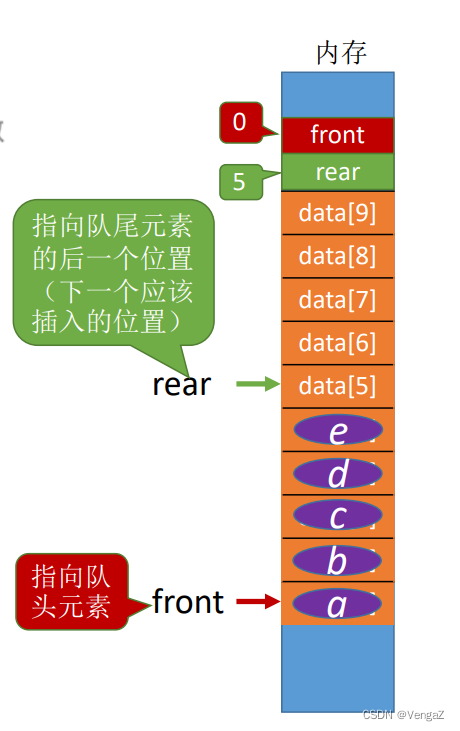
队头指针：指向队头元素
队尾指针：指向队尾元素的下一个位置

3.2.2.1 队列存储的基本操作

//队列的顺序存储类型
# define MaxSize 10;     //定义队列中元素的最大个数
typedef struct{
    ElemType data[MaxSize];   //用静态数组存放队列元素
                              //连续的存储空间，大小为
                              //MaxSize*sizeof(ElemType)
    int front, rear;          //队头指针和队尾指针
}SqQueue;

//初始化队列
void InitQueue(SqQueue &Q){
    //初始化时，队头、队尾指针指向0
    Q.rear = Q.front = 0;
}

void test{
    SqQueue Q;                //声明一个队列
    InitQueue(Q);
    //...
}

// 判空
bool QueueEmpty(SqQueue 0){
    if(Q.rear == Q.front)    //判空条件
        return true;
    else 
        return false;
}

1. 用静态数组存放队列元素，连续的存储空间，大小为MaxSize*sizeof(ElemType)
2. int front, rear; //队头指针和队尾指针
3. if(Q.rear == Q.front) //判空条件

用int类型表示数据在队伍的相对位置，相当于用数组的下标来表示元素的位置
front指向队头元素，rear指向下一个空缺的位置

3.2.2.2 循环队列$基本操作和判空方式$

定义：将循环队列臆造为一个环状的空间，即把存储队列元素的表从逻辑上视为一个环，称为循环队列。
基本操作：

a%b == a除以b的余数

初始：Q.front = Q.rear = 0;

队首指针进1：Q.front = (Q.front + 1) % MaxSize

队尾指针进1：Q.rear = (Q.rear + 1) % MaxSize —— 队尾指针后移，当移到最后一个后，下次移动会到第一个位置

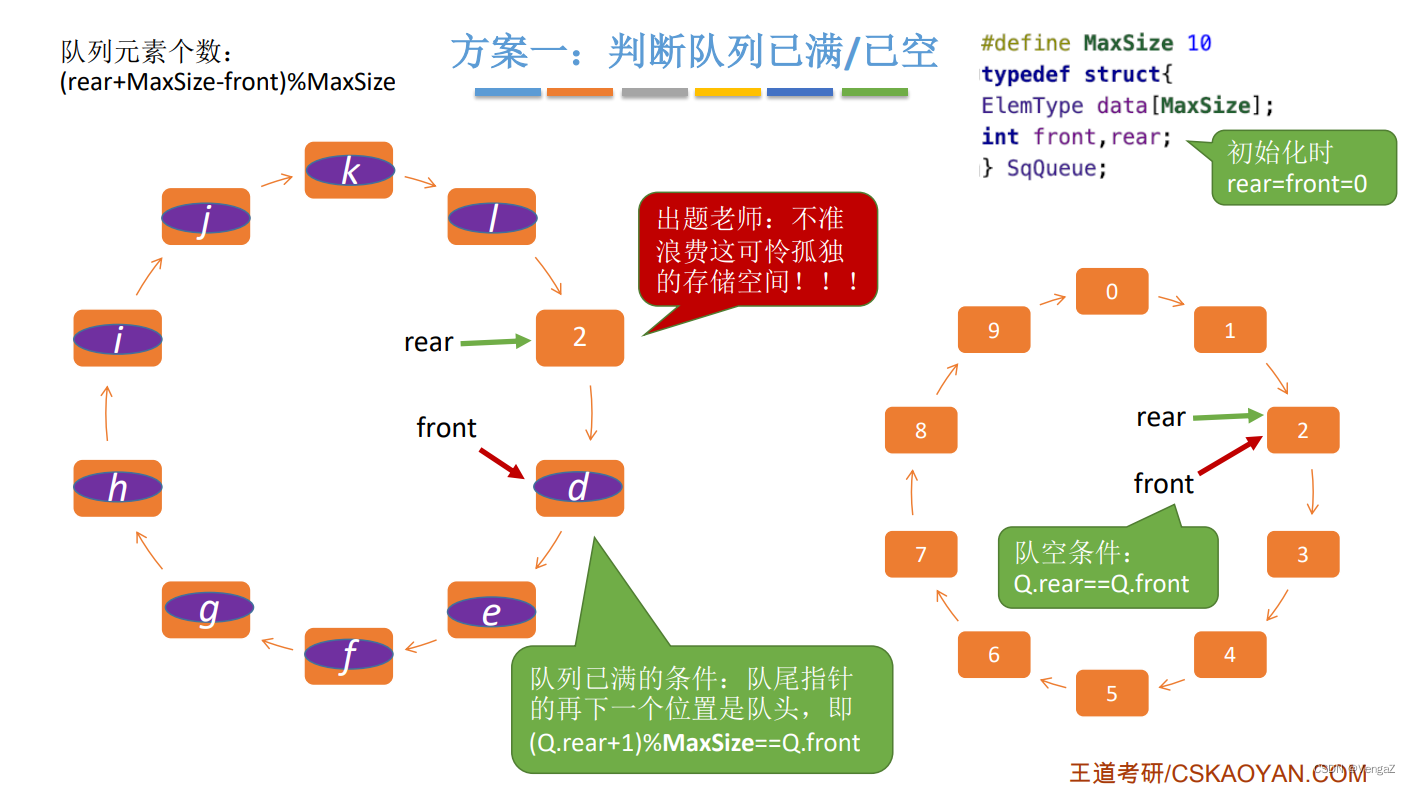
队列长度：(Q.rear + MaxSize - Q.front) % MaxSize

$重点是这个循环队列的判断空的方式，以下是几种方式，这些方式都是为了与$
$队列的判空条件Q.front=Q.rear；区分开$

方案一: 牺牲一个单元来区分队空和队满
队尾指针的再下一个位置就是队头，即 (Q.rear+1)%MaxSize == Q.front

循环队列——入队：只能从队尾插入（判满使用方案一）

bool EnQueue(SqQueue &Q, ElemType x){
    if((Q.rear+1)%MaxSize == Q.front)        //队满
        return false;
    Q.data[Q.rear] = x;                      //将x插入队尾
    Q.rear = (Q.rear + 1) % MaxSize;         //队尾指针加1取模

    return true;
}

循环队列——出队：只能让队头元素出队

//出队，删除一个队头元素，用x返回
bool DeQueue(SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front)              //队空报错
        return false;  

    x = Q.data[Q.front];
    Q.front = (Q.front + 1) % MaxSize; //队头指针后移动

    return true;
}

循环队列——获得队头元素

bool GetHead(SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front)              //队空报错
        return false;  

    x = Q.data[Q.front];
    return true;
}

方案二: 不牺牲存储空间，设置size
定义一个变量 size用于记录队列此时记录了几个数据元素，初始化 size = 0，进队成功 size++，出队成功size--，根据size的值判断队满与队空

队满条件：size == MaxSize

队空条件：size == 0

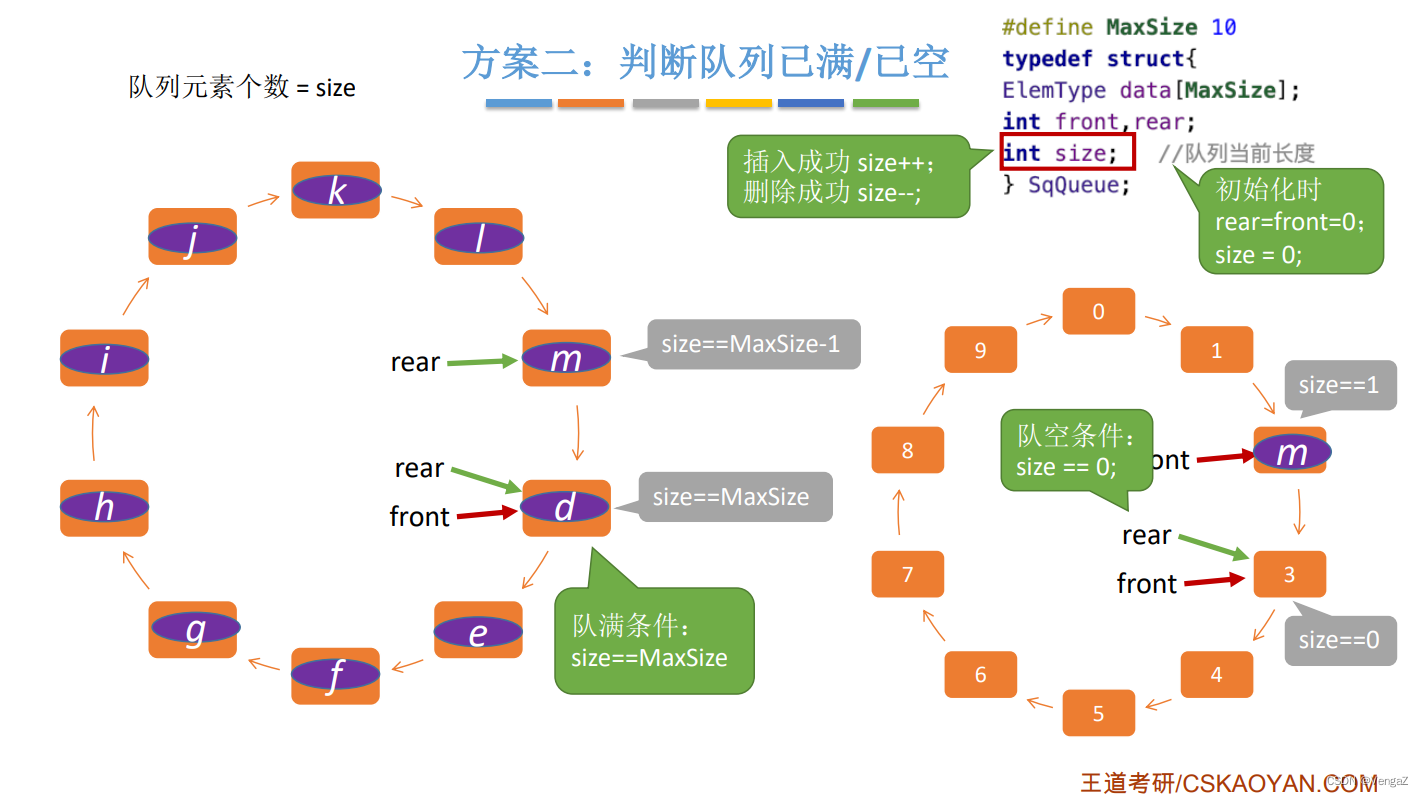
# define MaxSize 10;     
typedef struct{
    ElemType data[MaxSize];   
    int front, rear;        
    int size;               //队列当前长度
}SqQueue;

//初始化队列
void InitQueue(SqQueue &Q){
    Q.rear = Q.front = 0;
    size = 0;
}

方案三: 不牺牲存储空间，设置tag
定义一个变量 tag，tag = 0 --最近进行的是删除操作；tag = 1 --最近进行的是插入操作；

每次删除操作成功时，都令tag = 0；只有删除操作，才可能导致队空；
每次插入操作成功时，都令tag = 1；只有插入操作，才可能导致队满；
队满条件：Q.front == Q.rear && tag == 1
队空条件：Q.front == Q.rear && tag == 0

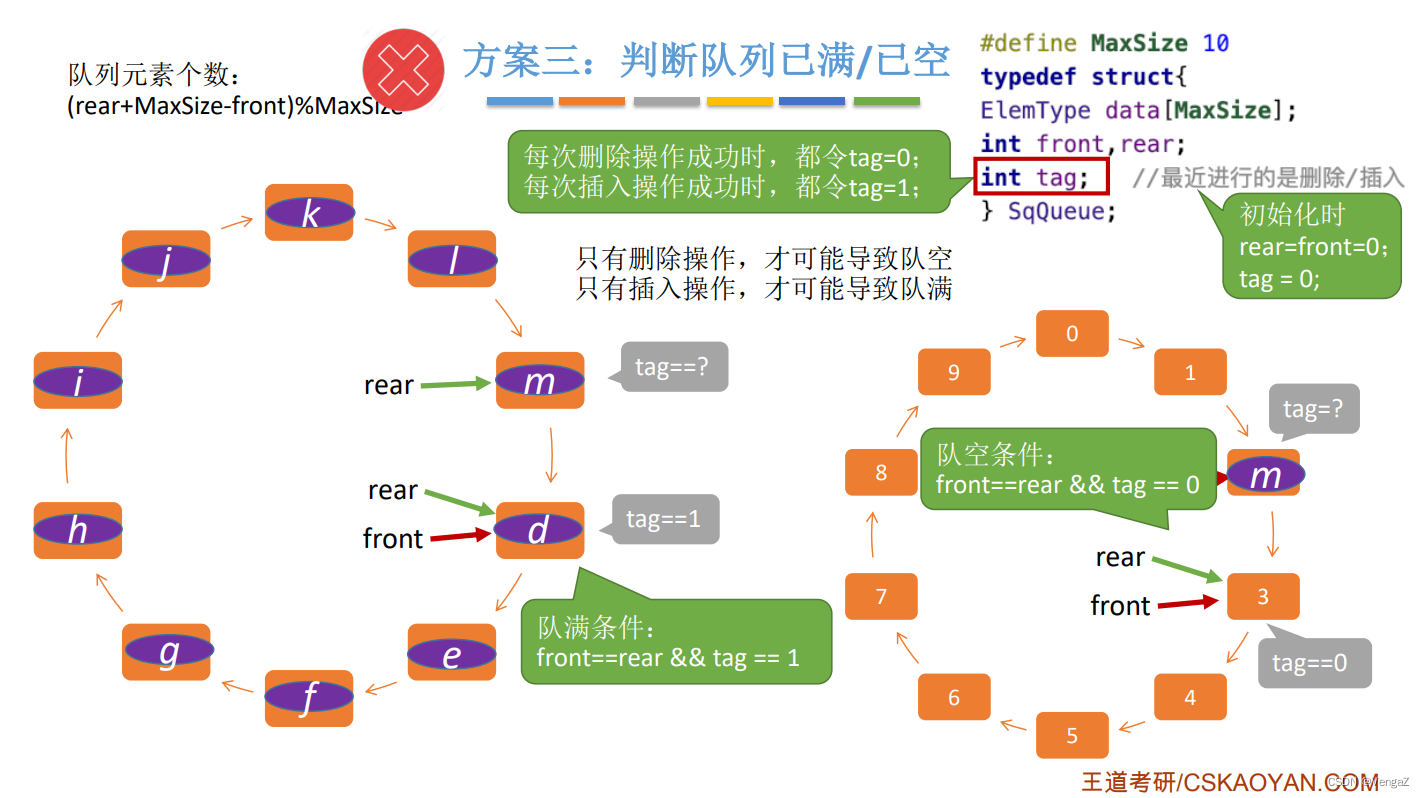
# define MaxSize 10;     
typedef struct{
    ElemType data[MaxSize];   
    int front, rear;        
    int tag;               //最近进行的是删除or插入
}SqQueue;

3.2.2.3 知识回顾

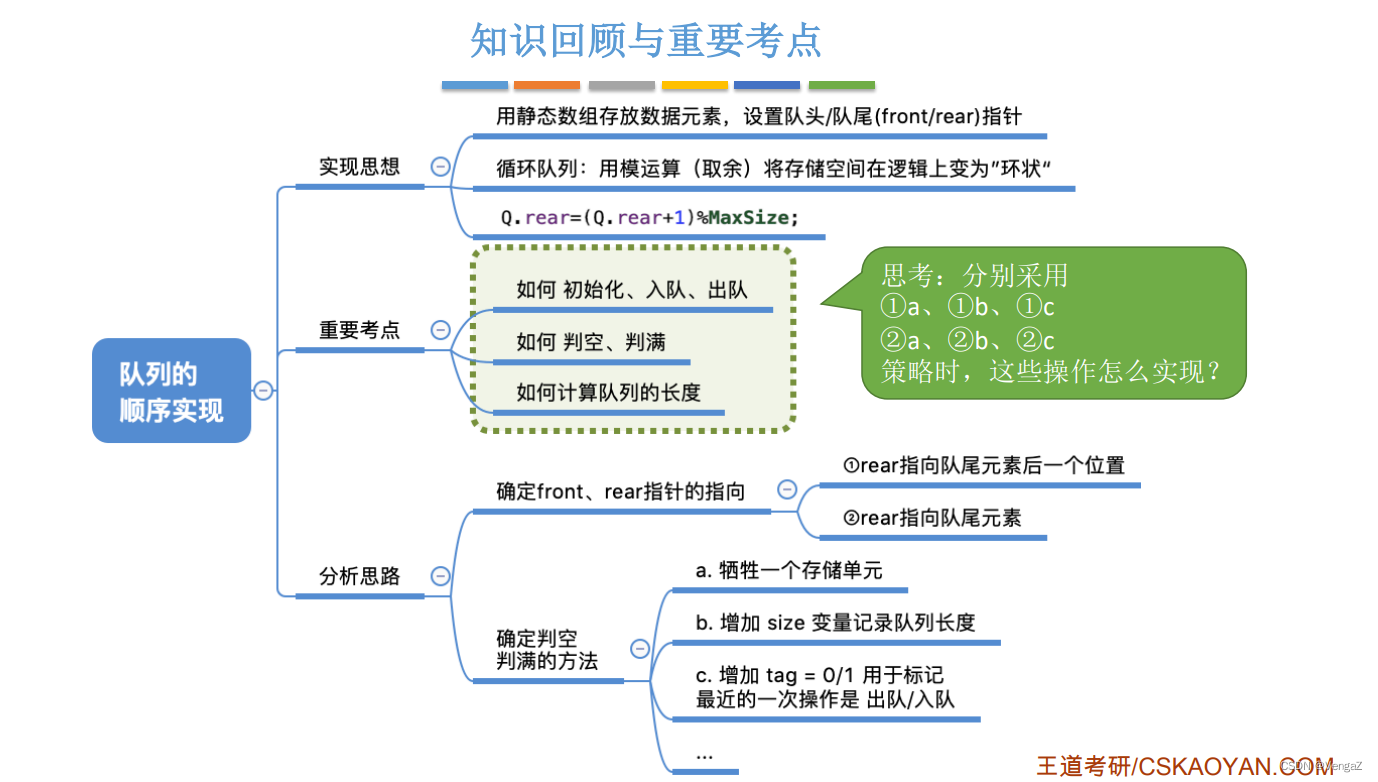
3.2.3 队列的链式存储结构

3.2.3.1定义

1.定义：队列的链式表示称为链队列，它实际上是一个同时带有队头指针和队尾指针的单链表。
链队列：用链表表示的队列，是限制仅在表头删除和表尾插入的单链表。
队列的链式存储类型可描述为:

typedef struct LinkNode{      //链式队列结点
    ElemType data;
    struct LinkNode *next;
}

typedef struct{               //链式队列
    LinkNode *front, *rear;   //队列的队头和队尾指针
}LinkQueue;

3.2.3.2链式队列的基本操作——带头结点

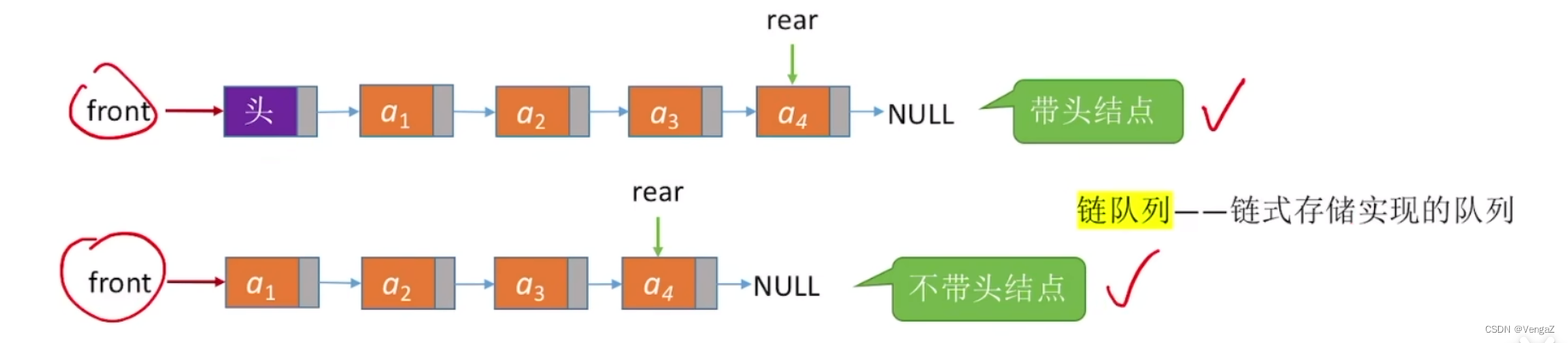
• 初始化 & 判空

void InitQueue(LinkQueue &Q){
    //初始化时，front、rear都指向头结点
    Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
    Q.front -> next = NULL;
}

//判断队列是否为空
bool IsEmpty(LinkQueue Q){
    if(Q.front == Q.rear)     //也可用 Q.front -> next == NULL
        return true;
    else
        return false;
}

• 入队操作

//新元素入队 (表尾进行)
void EnQueue(LinkQueue &Q, ElemType x){
    LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode)); //申请一个新结点
    s->data = x;
    s->next = NULL;     //s作为最后一个结点，指针域指向NULL
    Q.rear->next = s;   //新结点插入到当前的rear之后
    Q.rear = s;         //表尾指针指向新的表尾
}

• 出队操作

//队头元素出队
bool DeQueue(LinkQueue &Q, ElemType &x){
    if(Q.front == Q.rear)
        return false;                    //空队
    
    LinkNode *p = Q.front->next;         //p指针指向即将删除的结点 (头结点所指向的结点)
    x = p->data;
    Q.front->next = p->next;             //修改头结点的next指针
    if(Q.rear == p)                      //此次是最后一个结点出队
        Q.rear = Q.front;                //修改rear指针
    free(p);                             //释放结点空间

    return true;
}

• 队列满的条件
  顺序存储：预分配存储空间
  链式存储：一般不会队满，除非内存不足

• 计算链队长度 (遍历链队)
  设置一个int length 记录链式队列长度

---

3.2.3.3 不带头结点的相关操作

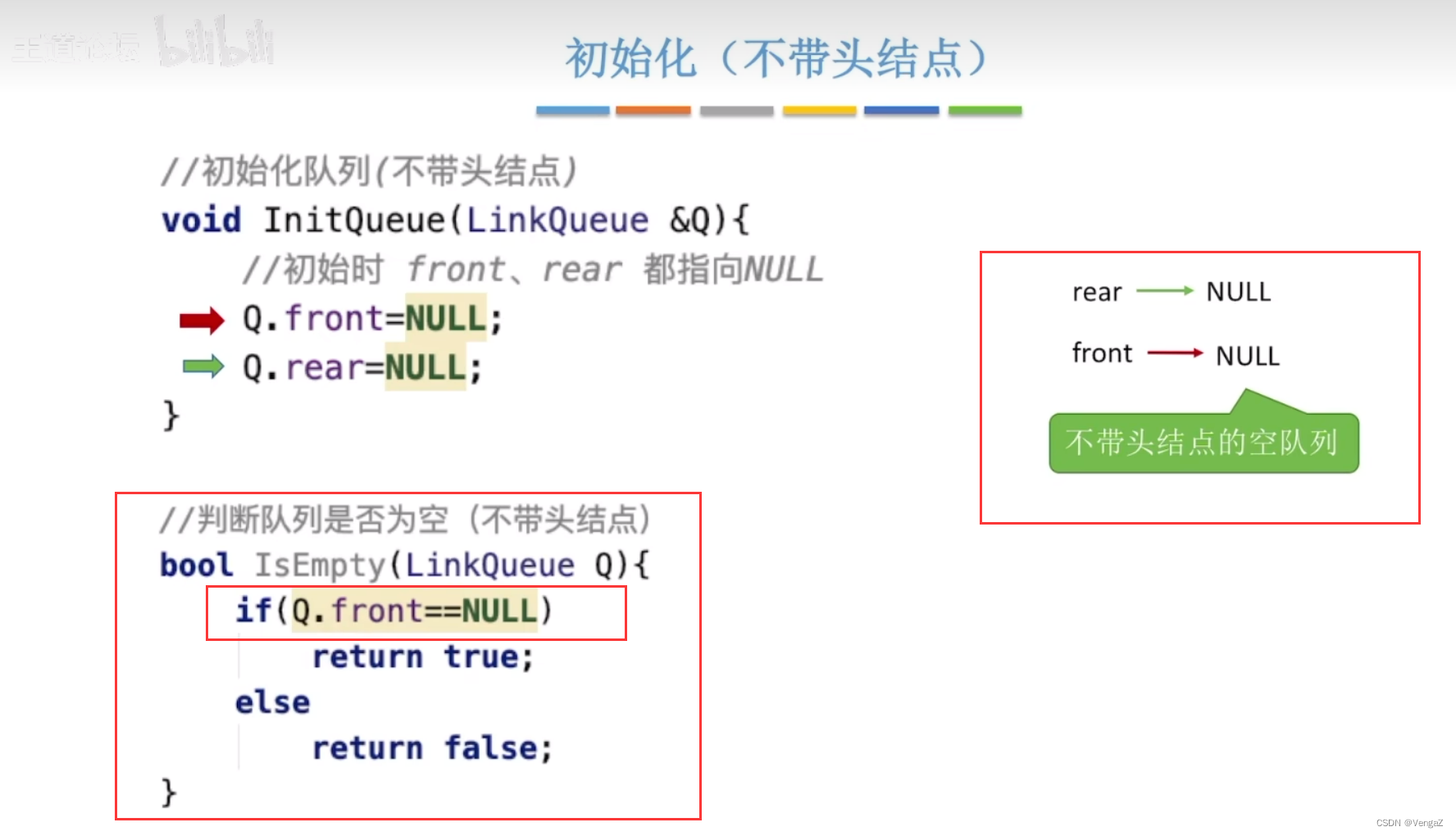
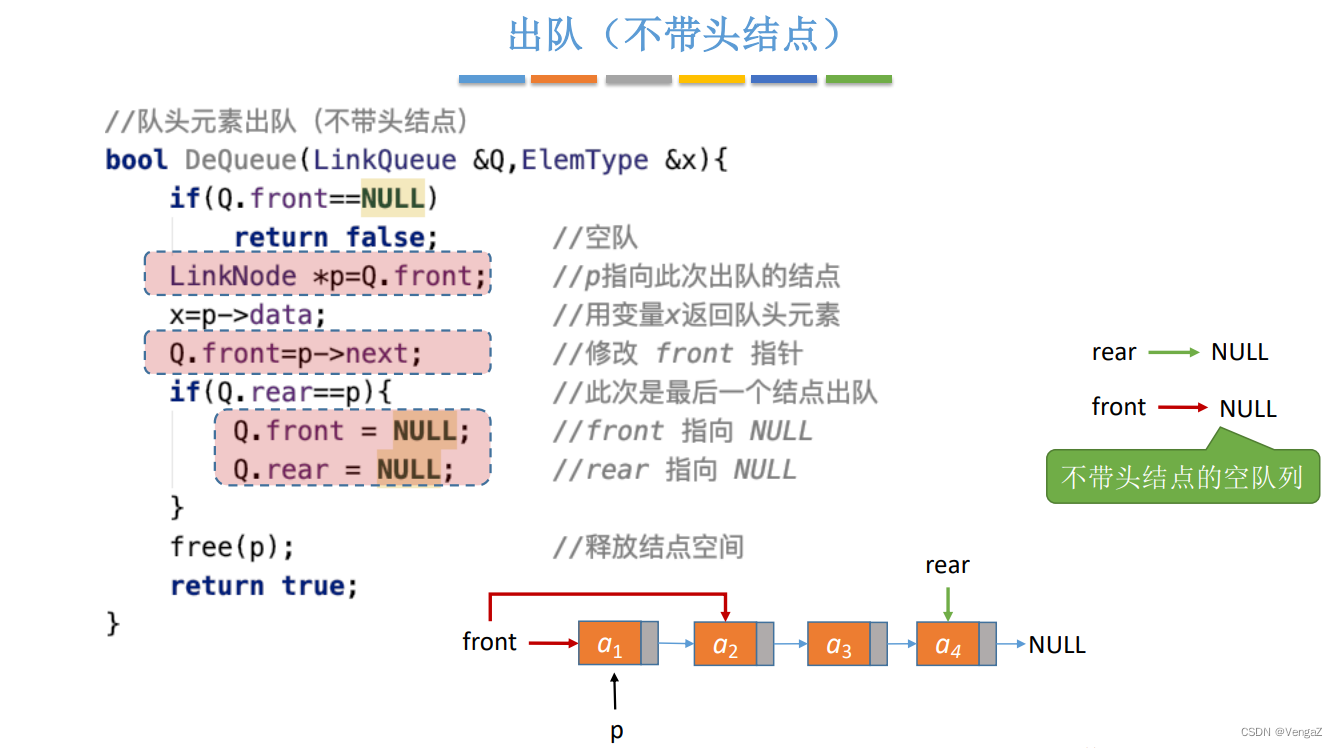
3.2.4双端队列

0. 限制输入输出问题（需要再验证）

对于双端队列的限制输出以及输出问题，做以下考虑

• 限制输入的，就意味着单边输入，注意输入顺序，怎么输入就怎么按照什么顺序写下去，再去左右判断是否可以输出
• 限制输出的，就意味着单边输出，注意输出顺序，按照输入顺序的第一个，选项中左右寻找临近的输入顺序，找得到则合法

1.定义

双端队列是指允许两端都可以进行入队和出队操作的队列

• 双端队列允许从两端插入、两端删除的线性表；
• 如果只使用其中一端的插入、删除操作，则等同于栈；
• 输入受限的双端队列：允许一端插入，两端删除的线性表；
• 输出受限的双端队列：允许两端插入，一端删除的线性表；

栈合法的序列，双端序列也合法（只用一边就是一个栈），所以只要考虑不合法的那些

3.2.5循环队列

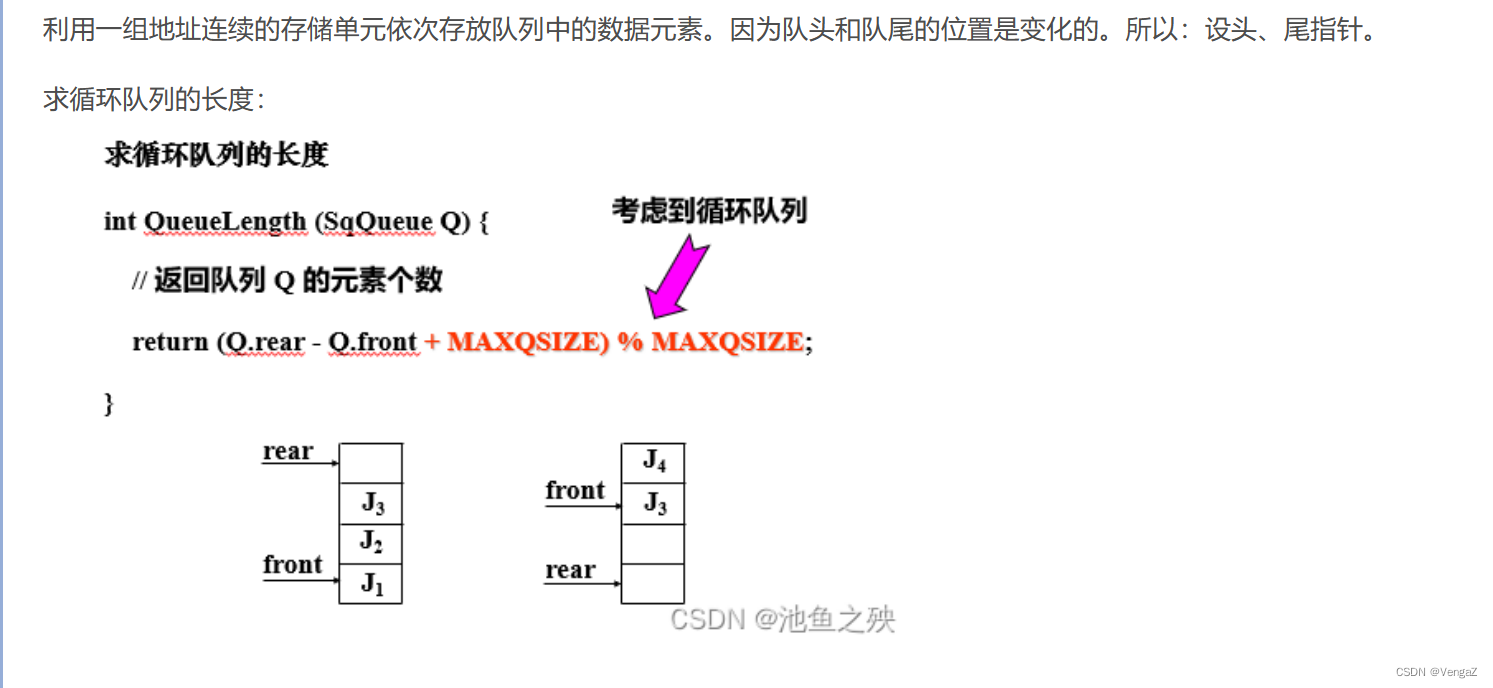
3.3栈的应用

3.3.1栈在括号匹配中的应用

用栈实现括号匹配

• ((())) 最后出现的左括号最先被匹配 (栈的特性—LIFO);

• 遇到左括号就入栈;

• 遇到右括号，就“消耗”一个左括号 (出栈);

匹配失败情况：

• 扫描到右括号且栈空，则该右括号单身;

• 扫描完所有括号后，栈非空，则该左括号单身;

• 左右括号不匹配;

流程图

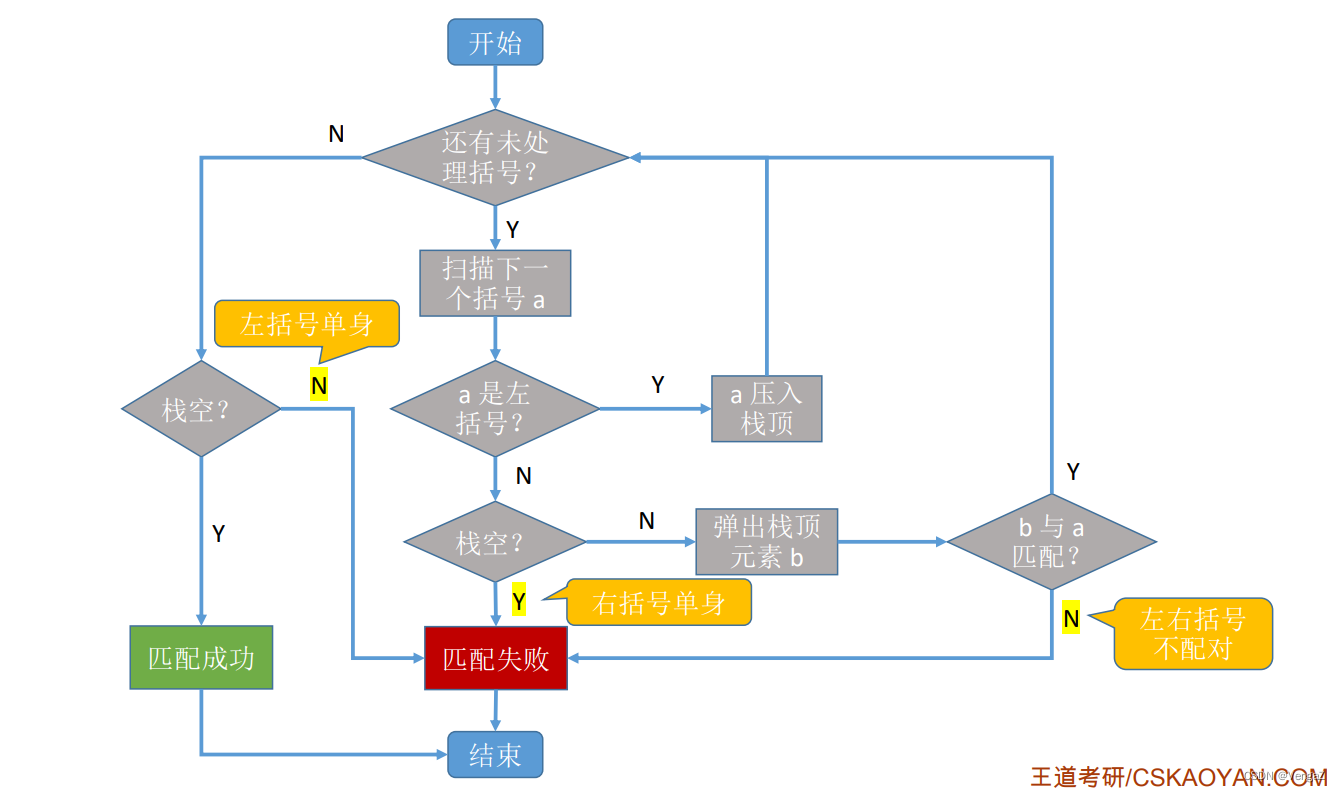
算法代码

#define MaxSize 10   

typedef struct{
    char data[MaxSize];
    int top;
} SqStack;

//初始化栈
InitStack(SqStack &S)

//判断栈是否为空
bool StackEmpty(SqStack &S)

//新元素入栈
bool Push(SqStack &S, char x)

//栈顶元素出栈，用x返回
bool Pop(SqStack &S, char &x)



bool bracketCheck(char str[], int length){
    SqStack S;      //声明
    InitStack(S);   //初始化栈

    for(int i=0; i<length; i++){
        if(str[i] == '(' || str[i] == '[' || str[i] == '{'){
            Push(S, str[i]);       //扫描到左括号，入栈
        }else{
            if(StackEmpty(S))      //扫描到右括号，且当前栈空
                return false;      //匹配失败
            
            char topElem;          //存储栈顶元素
            Pop(S, topElem);       //栈顶元素出栈

            if(str[i] == ')' && topElem != '(' )
                return false;

            if(str[i] == ']' && topElem != '[' )
                return false;

            if(str[i] == '}' && topElem != '{' )
                return false;       
        }
    }

    StackEmpty(S);                //栈空说明匹配成功
}

3.3.2栈在表达式求值中的应用

1. 中缀表达式 (需要界限符)

运算符在两个操作数中间:

① a + b
② a + b - c
③ a + b - c*d
④ ((15 ÷ (7-(1+1)))×3)-(2+(1+1))
⑤ A + B × (C - D) - E ÷ F

2. 后缀表达式 (逆波兰表达式)

运算符在两个操作数后面:

① a b +
② ab+ c - / a bc- +
③ ab+ cd* -
④ 15 7 1 1 + - ÷ 3 × 2 1 1 + + -
⑤ A B C D - × + E F ÷ - (机算结果)
  A B C D - × E F ÷ - + (不选择)

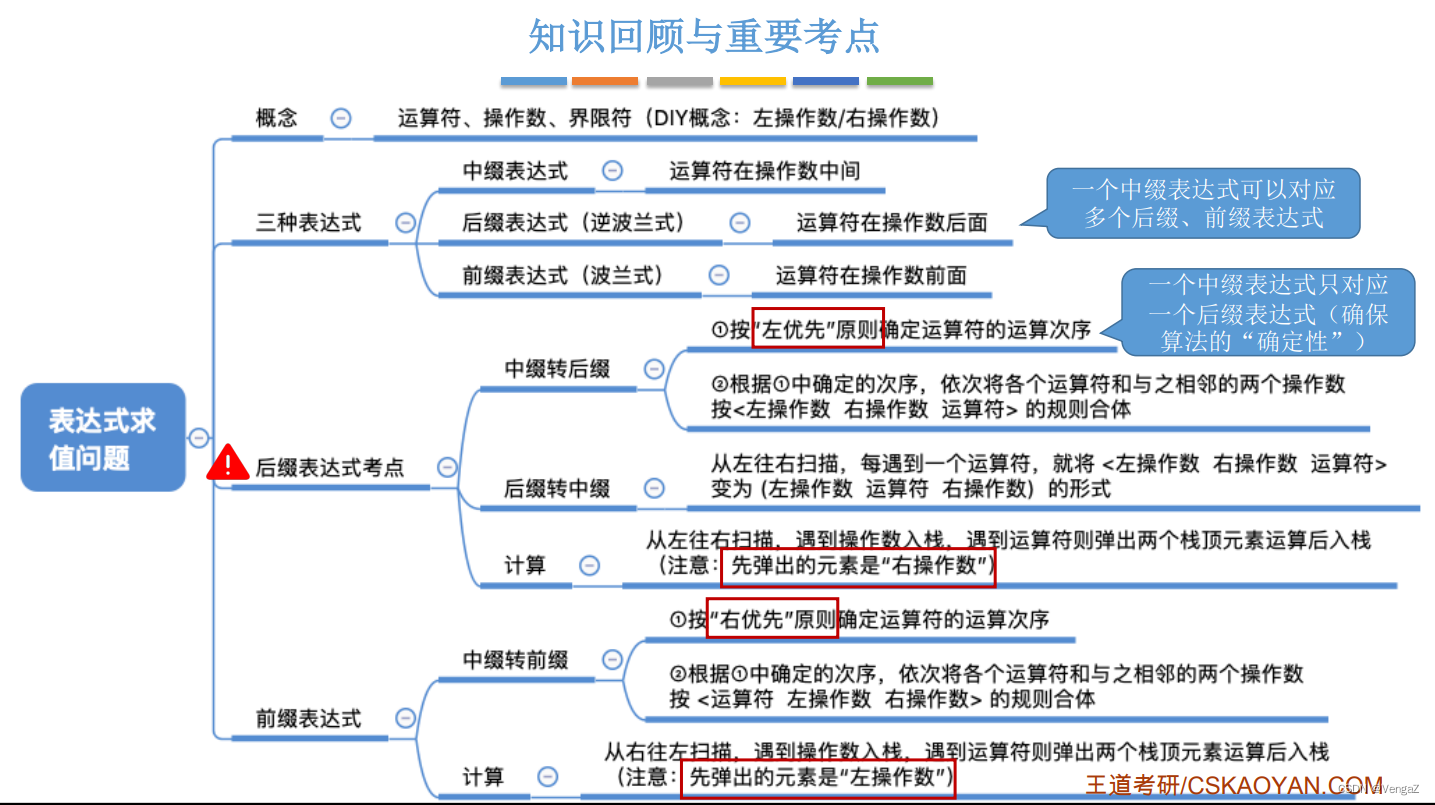
中缀表达式转后缀表达式-手算

• 步骤1： 确定中缀表达式中各个运算符的运算顺序

• 步骤2： 选择下一个运算符，按照[左操作数 右操作数 运算符]的方式组合成一个新的操作数

• 步骤3： 如果还有运算符没被处理，继续步骤2

“左优先”原则: 只要左边的运算符能先计算，就优先算左边的 (保证运算顺序唯一)；

中缀：A + B - C * D / E + F
       ①   ④   ②   ③   ⑤     
后缀：A B + C D * E / - F +

重点：中缀表达式转后缀表达式-机算

初始化一个栈，用于保存暂时还不能确定运算顺序的运算符。从左到右处理各个元素，直到末尾。可能遇到三种情况:

• 遇到操作数: 直接加入后缀表达式。
• 遇到界限符: 遇到 ‘(’ 直接入栈; 遇到 ‘)’ 则依次弹出栈内运算符并加入后缀表达式，直到弹出 ‘(’ 为止。注意: ‘(’ 不加入后缀表达式。
• 遇到运算符: 依次弹出栈中优先级高于或等于当前运算符的所有运算符，并加入后缀表达式，若碰到 ‘(’ 或栈空则停止。之后再把当前运算符入栈。

按上述方法处理完所有字符后，将栈中剩余运算符依次弹出，并加入后缀表达式。

重点：后缀表达式的计算—机算

先出栈的是“右操作数”

3.前缀表达式 (波兰表达式)

运算符在两个操作数前面:

① + a b
② - +ab  c
③ - +ab *cd

中缀表达式转前缀表达式—手算

• 步骤1： 确定中缀表达式中各个运算符的运算顺序

• 步骤2： 选择下一个运算符，按照[运算符 左操作数 右操作数]的方式组合成一个新的操作数

• 步骤3： 如果还有运算符没被处理，就继续执行步骤2

“右优先”原则: 只要右边的运算符能先计算，就优先算右边的;

中缀：A + B * (C - D) - E / F
       ⑤   ③    ②    ④   ①
前缀：+ A - * B - C D / E F

注意: 先出栈的是“左操作数”

4.中缀表达式的计算(用栈实现)

两个算法的结合： 中缀转后缀 + 后缀表达式的求值

初始化两个栈，操作数栈 和运算符栈

若扫描到操作数，压人操作数栈

若扫描到运算符或界限符，则按照“中缀转后缀”相同的逻辑压入运算符栈 (期间也会弹出运算符，每当弹出一个运算符时，就需要再弹出两个操作数栈的栈项元素并执行相应运算，运算结果再压回操作数栈)

5. 知识回顾

3.3.3栈在递归中的应用

迷宫求解也用到栈

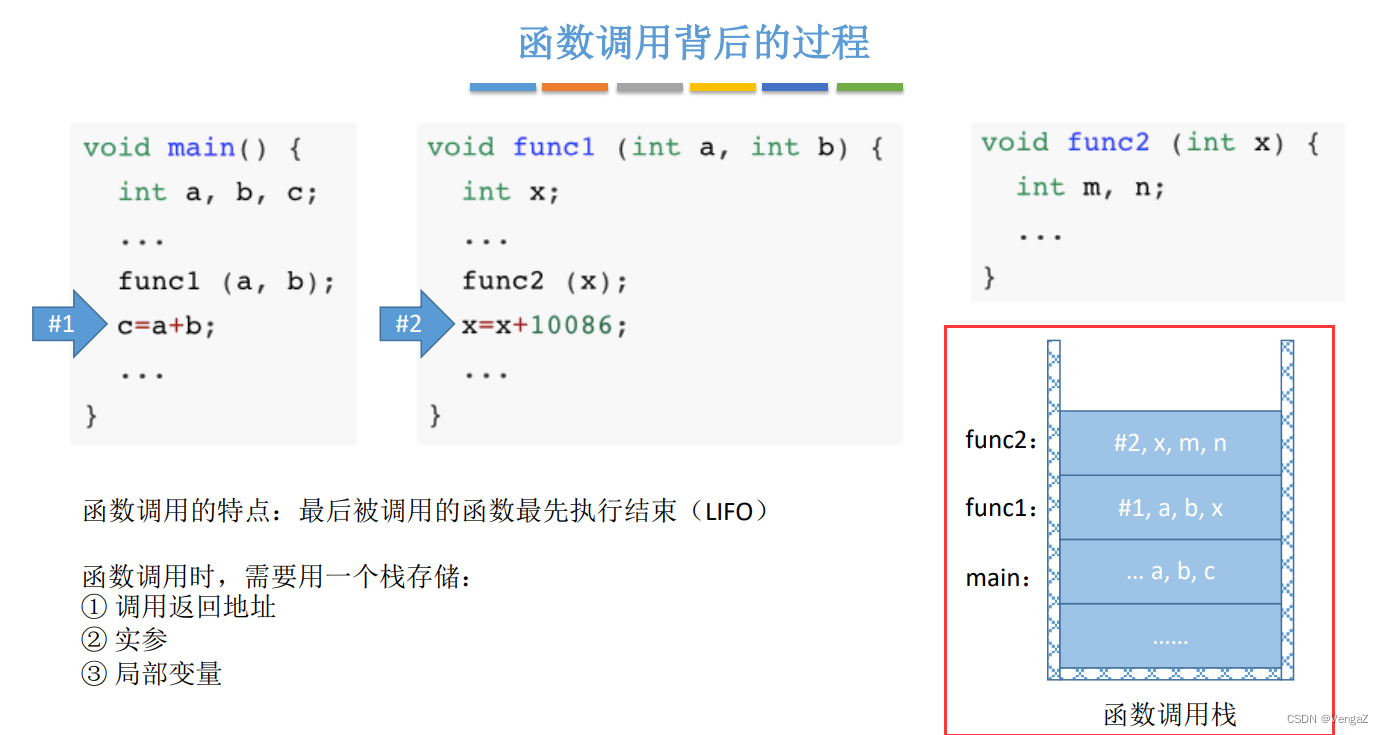
函数调用的特点：=最后被调用的函数最先执行结束(LIFO)

函数调用时，需要用一个栈存储：

• 调用返回地址（下一条指令的地址）
• 实参（传递的）
• 局部变量（自己的）

递归调用时，函数调用栈称为 “递归工作栈”:

• 每进入一层递归，就将递归调用所需信息压入栈顶；
  每退出一层递归，就从栈顶弹出相应信息；

缺点：太多层递归可能回导致栈溢出（空间复杂度升高）；也可能含有很多重复计算过程

适合用“递归”算法解决：可以把原始问题转换为属性相同，但规模较小的问题；

调用过程

3.3.4 队列的应用

树的层次遍历、图的广度优先遍历、操作系统FCFS（先来先服务）

3.4 数组和特殊矩阵

矩阵定义： 一个由m*n个元素排成的m行(横向)n列(纵向)的表。
矩阵的常规存储：将矩阵描述为一个二维数组。

3.4.1数组的存储结构

1. 一维数组
   Elemtype a[10];

各数组元素大小相同，物理上连续存放；

起始地址：LOC

数组下标：默认从0开始！

数组元素 a[i] 的存放地址 = LOC + i × sizeof(ElemType)

2. 二维数组

Elemtype b[2][4]; //2行4列的二维数组

行优先/列优先存储优点：实现随机存储

起始地址：LOC

M行N列的二维数组 b[M][N] 中，b[i][j]的存储地址：

行优先存储: LOC + (i×N + j) × sizeof(ElemType)
列优先存储：LOC + (j×M + i) × sizeof(ElemType)

3.4.2普通矩阵的存储

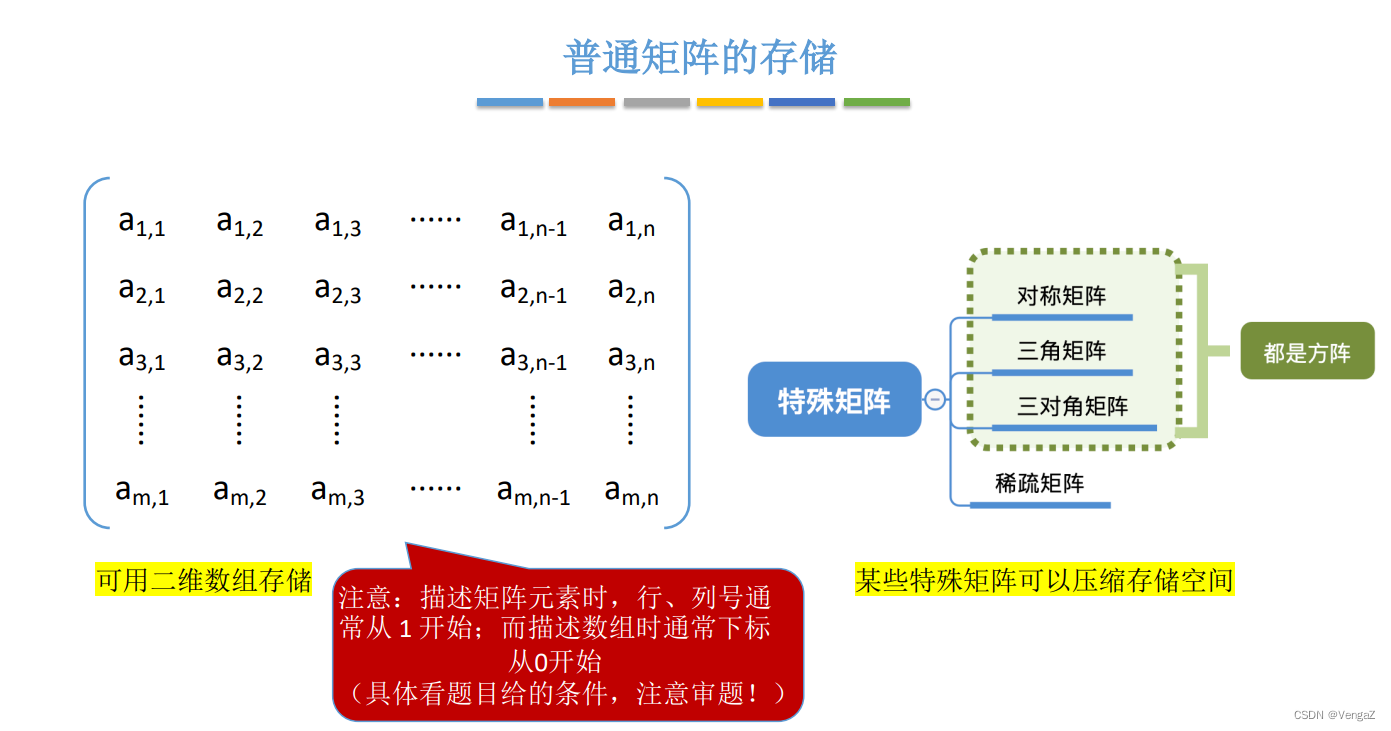
二维数组存储：

• 描述矩阵元素时，行、列号通常从1开始；
• 描述数组时，通常下标从 0 开始；

3.4.3特殊矩阵的存储

特殊矩阵——压缩存储空间（只存有用的数据）

矩阵的压缩存储：为多个相同的非零元素只分配一个存储空间；对零元素不分配空间。

1. 对称矩阵(方阵)

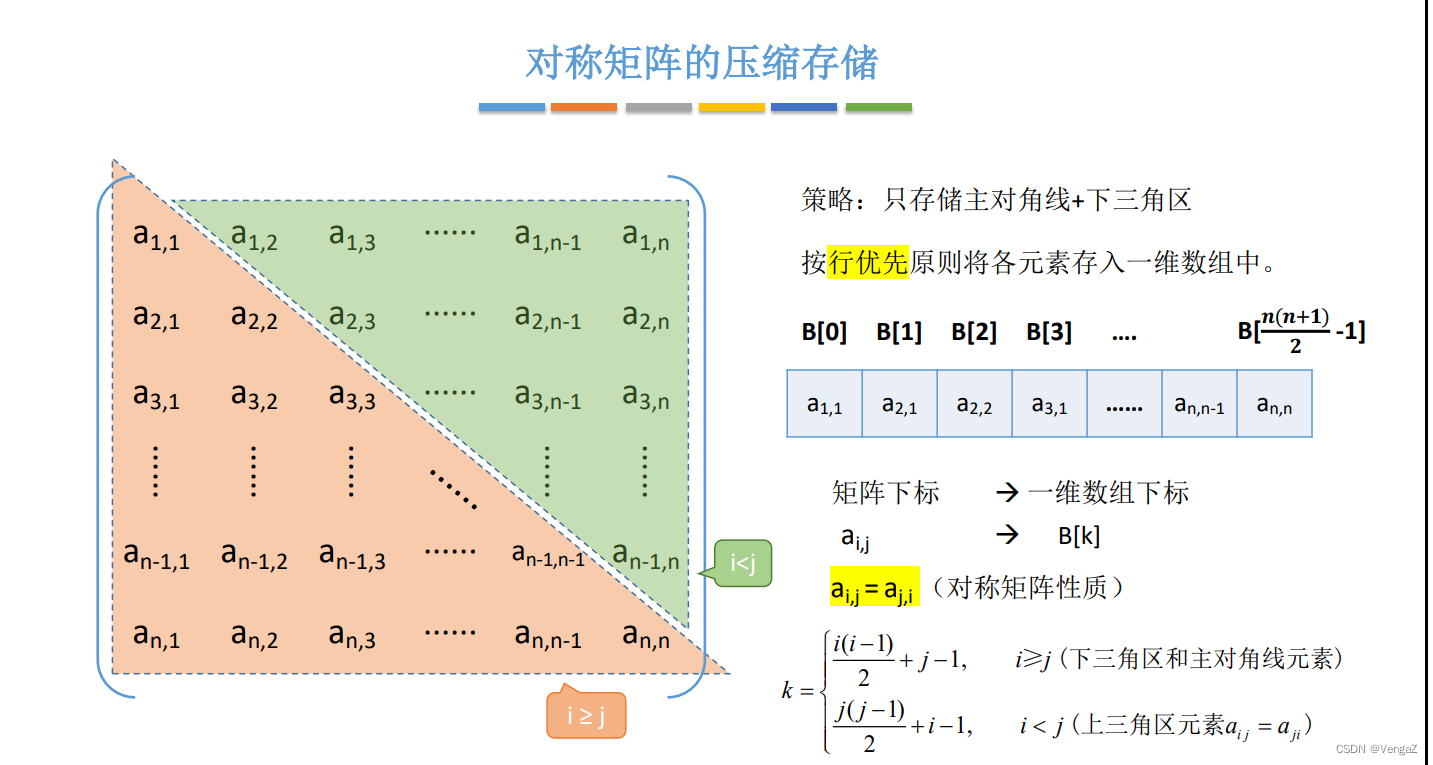
列优先：

• n >1
  n+ (n-1)+ ······+(i-j)+1

• n = 1
  i-j+1

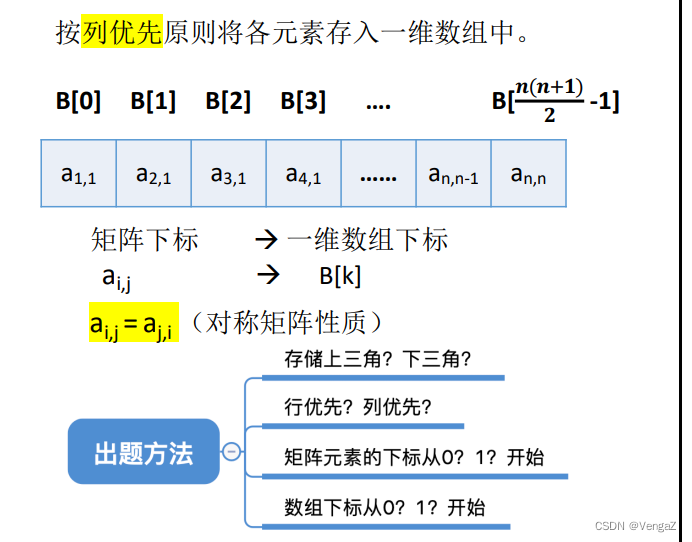
2. 三角矩阵(方阵)

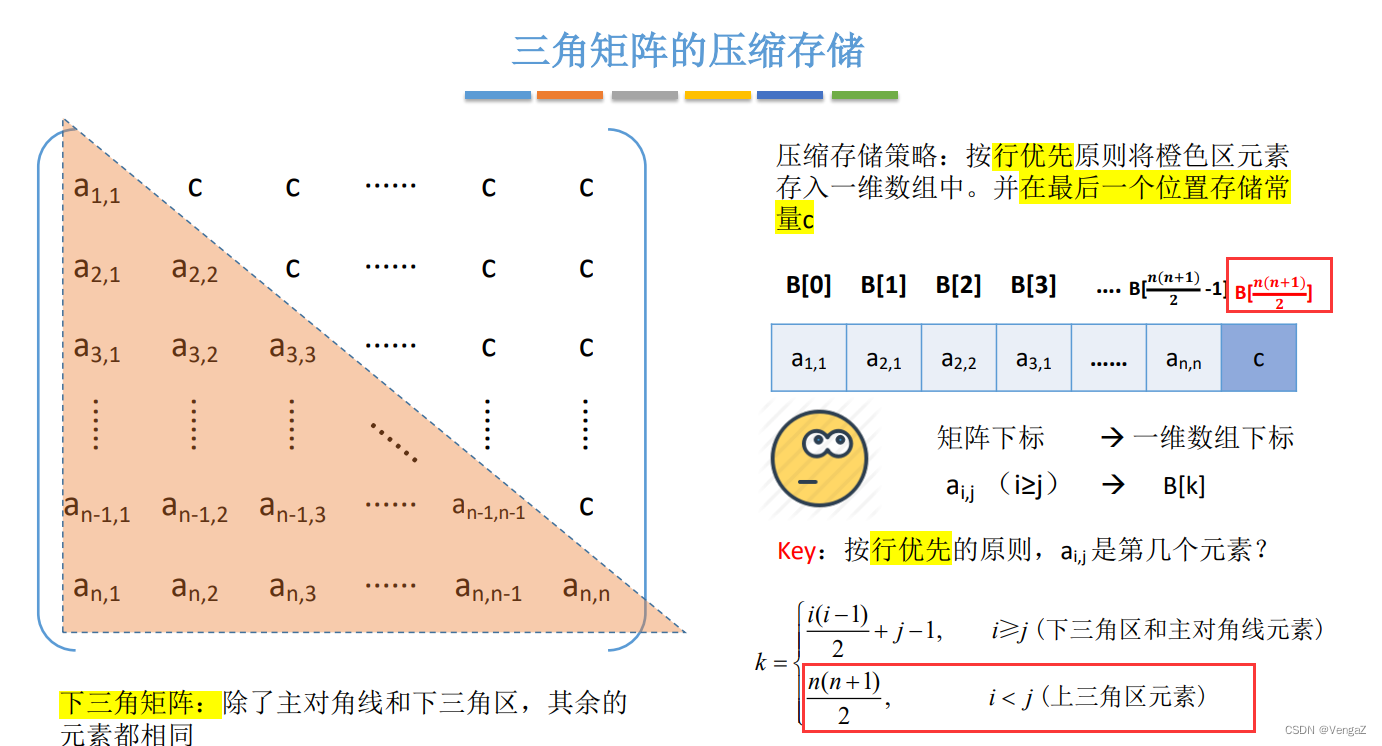
n + (n-1) +······(n-i+1) +(j-i)

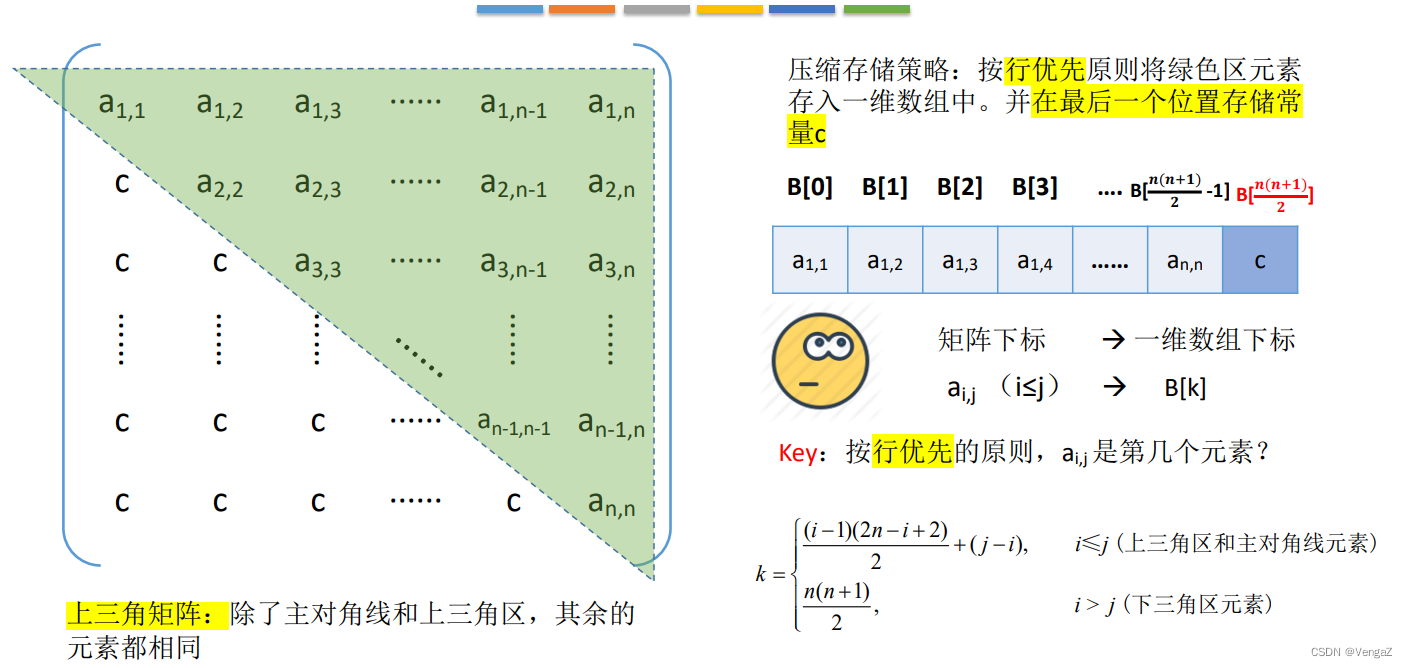
3. 三对角矩阵(方阵)带状

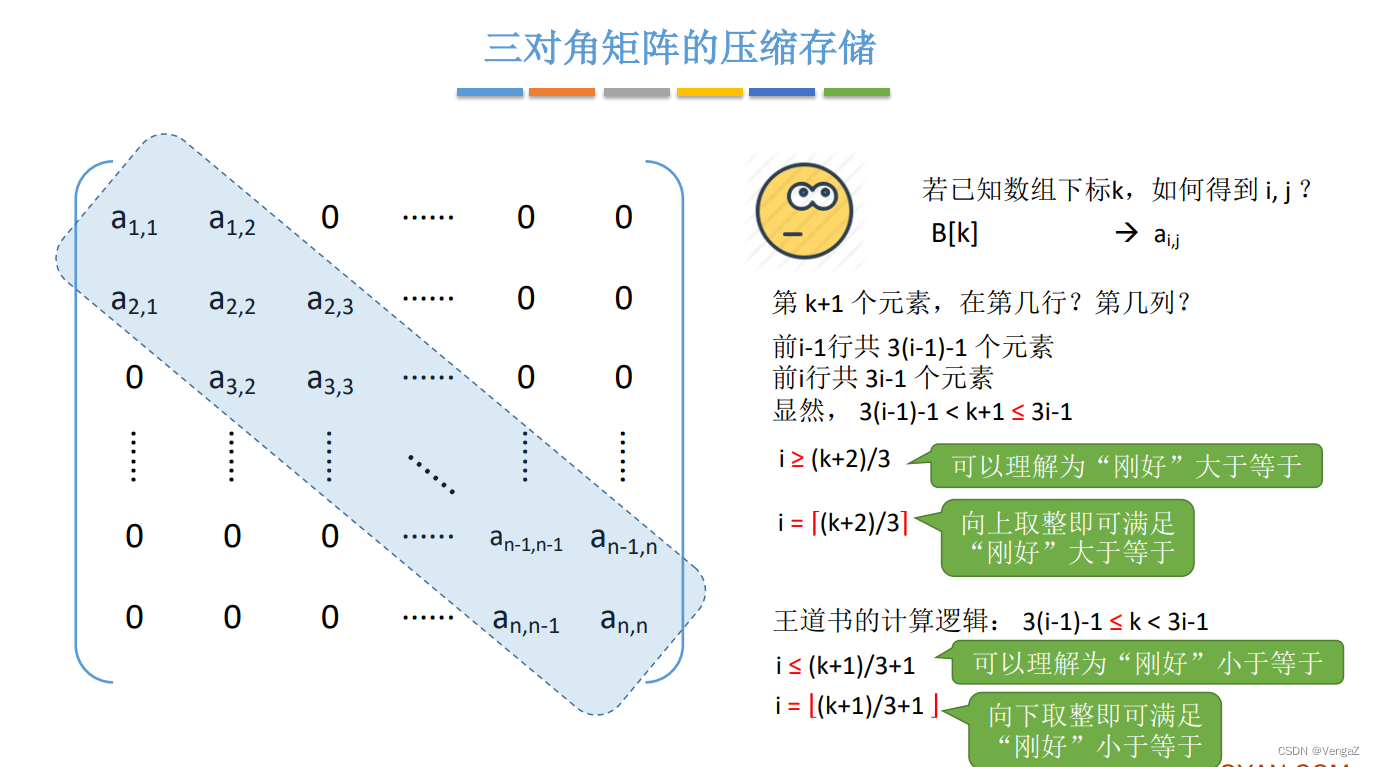
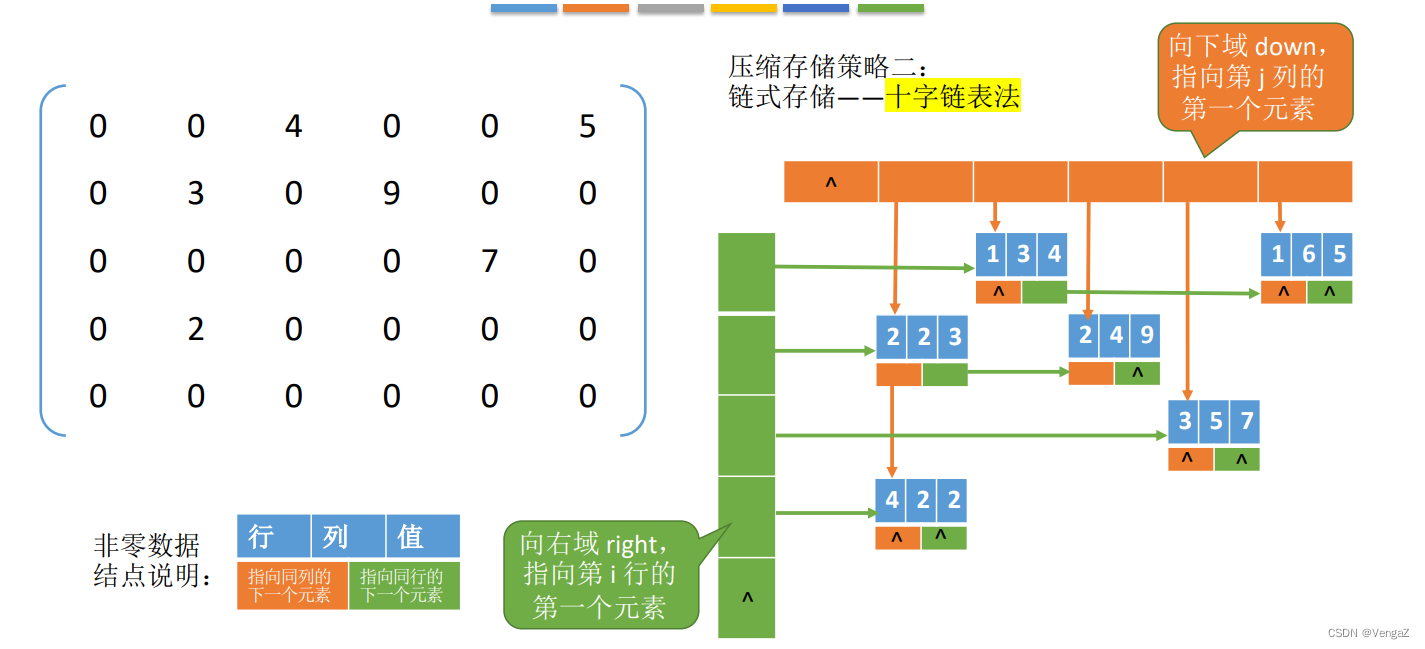
4. 稀疏矩阵

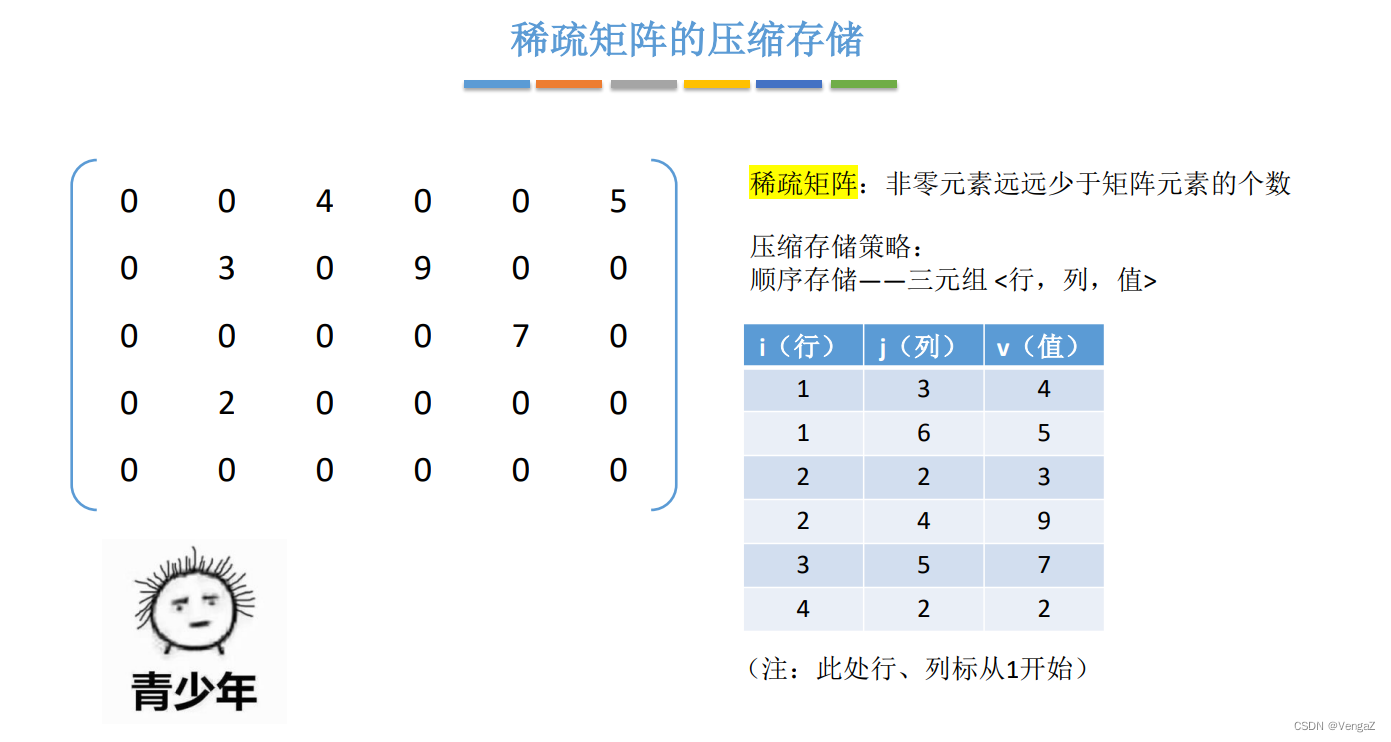
设在mn的矩阵中有t个非零元素，令c=t/(mn),当c<=0.05时称为稀疏矩阵。
压缩存储原则：存各非零元的值、行列位置和矩阵的行列数。