高等数学中求间断点是一项重要的技巧,特别适用于分析函数的性质和图像的特征。在本文中,我们将深入探讨如何在给定函数中找到间断点,并解释其数学原理和实际应用。
什么是间断点?
在高等数学中,间断点是指函数在某个点上无法连续的情况。在该点附近,函数可能发生跳跃、断裂或趋近于无穷大。在解析函数的特性时,我们特别关注间断点,因为它们能够揭示函数的突变和奇异性。
如何求间断点?
要求解间断点,首先需要找到函数的定义域,并确定其中的奇点(函数不连续的点)。然后,针对这些奇点,分别使用以下方法来判断是否是间断点:
1. 第一类间断点:如果在奇点x=a处,函数存在有限的左右极限(LHL和RHL)
f(x)在x处不存在,但x处左右极限存在且相等,则为可去间断点
f(x)在x处不存在,但x处左右极限存在但不相等,则为跳跃间断点
两者都为第一类间断点
2. 第二类间断点:如果在奇点x=a处,函数的左右极限至少有一个不存在或者趋于无穷大
左右极限至少有一个不存在且等于无穷,则x=a为无穷间断点
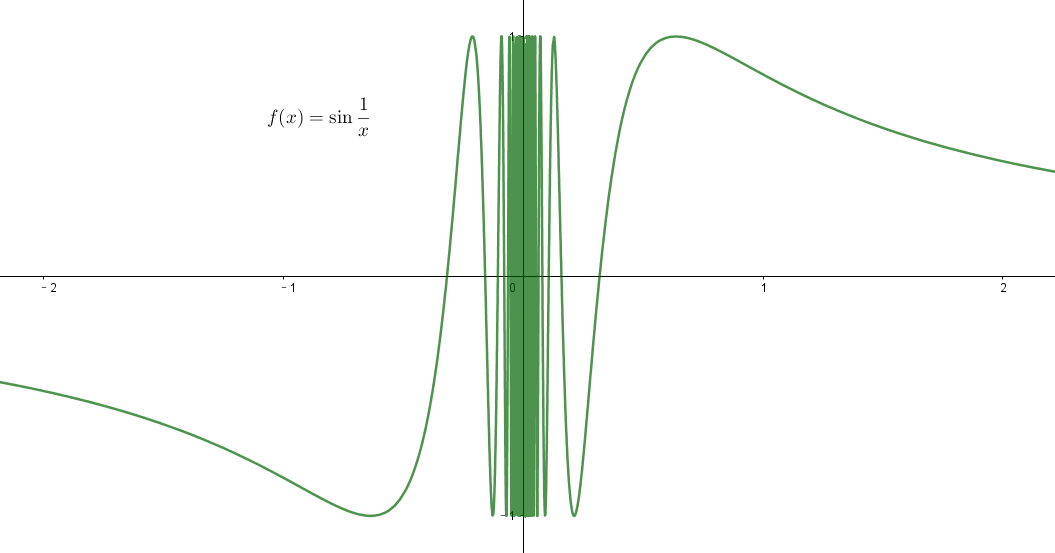
左右极限至少有一个不存在且振荡,则x=a为振荡间断点
两者都为第二类间断点
举例说明:
考虑函数f(x) = (x^2 - 4) / (x - 2)。首先,我们需要确定函数的定义域。显然,当x=2时,分母为零,因此函数在x=2处不定义。
1. 第一类间断点:计算在x=2处的左右极限。
LHL (x→2-) = lim (x→2-) [(x^2 - 4) / (x - 2)] = lim (x→2-) [(x+2)] = 4
RHL (x→2+) = lim (x→2+) [(x^2 - 4) / (x - 2)] = lim (x→2+) [(x+2)] = 4
左右极限存在,所以x=2是函数的第一类间断点。
2. 第二类间断点:考虑在x=0处的极限。
LHL (x→0-) = lim (x→0-) [(x^2 - 4) / (x - 2)] = lim (x→0-) [(4 - x^2) / (2 - x)] = -∞
RHL (x→0+) = lim (x→0+) [(x^2 - 4) / (x - 2)] = lim (x→0+) [(4 - x^2) / (2 - x)] = +∞
由于LHL和RHL的值一个趋近于负无穷大,一个趋近于正无穷大,因此x=0是函数的第二类间断点。
应用实例:
求解函数的间断点在实际问题中非常有用。例如,在经济学中,间断点可能表示某个商品价格的剧烈变动,影响市场供需的平衡;在物理学中,间断点可能对应某个过程中的异常现象,揭示系统的不稳定性。通过深入了解函数的间断点,我们可以更好地理解和预测自然界和社会现象中的突变和奇异性。
结论:
在高等数学中,求解函数的间断点是一项重要的技巧,有助于分析函数的性质和图像的特征。通过寻找函数的奇点并判断其类型,我们可以准确地确定间断点,并将其应用于各种实际问题中。深入理解函数的间断点有助于我们更好地理解和解释数学背后的自然和社会现象。