一篇文章帮你弄懂邻接矩阵，邻接表和链式前向星的区别

前言：

在学C++的时候，面对各种各样的存图方式，脑子都大了不少，各种算法还在向我冲来，结果一个邻接矩阵/邻接表/链表轻松给了我一下暴击就直接让我KO了，趁着脑子还算清楚，详细的介绍下这三种存图方式的本质与代码实现。

思路实现：

链式前向星、邻接矩阵适合存稠密图，而邻接表则适合存稀疏图，做题时可根据不同的数据范围来酌情选择三种方式来存储图。
既然提到了图，那么下面先来介绍一下。

一、图是什么？

图是一种数据结构，对于初学者来说，可以理解图就是有许多点用边连起来就叫做图。
图又分无向图和有向图，无向图即指两个点之间没有明确的指向性，两个点可以互相访问，遍历。
而有向图则于此不同，在输入完指向性后计算机只能按照先前建好的有向图进行遍历。

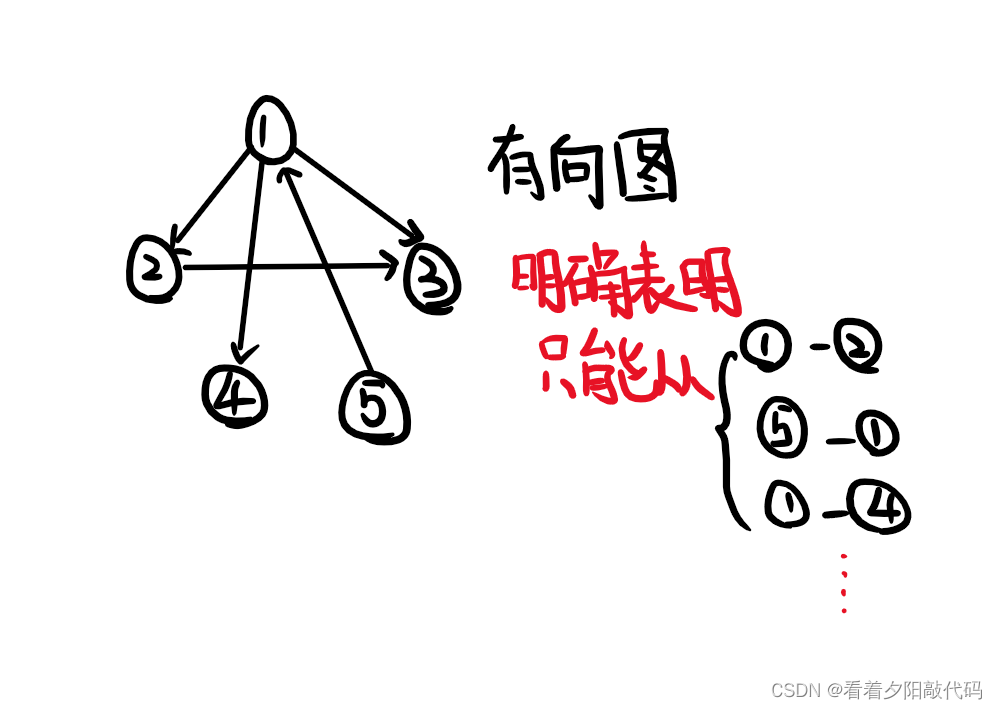
在这里插入图片描述
两个图较为相似，但是有些细节还是非常不同的。但是有向图和无向图的输入是一模一样，意思却略有不同，这里拿上图举例：
这里我们假设图中从u-v有一条边，则两图的输入均为：

1	2
1	4
5	1
1	3

这里拿第一行的"1 2"举个例子；
在无向图中，我可以从①号节点去访问②号节点，也可以从②号节点去访问①号节点；
在有向图中：因为输入循序是先‘1’后‘2’，所以在遍历和访问图的过程中只能从①号节点去访问②号节点。
除去边的关系，图还有一重要东西就是边权，简单来说就是就是访问两个节点所需要花的"代价"。
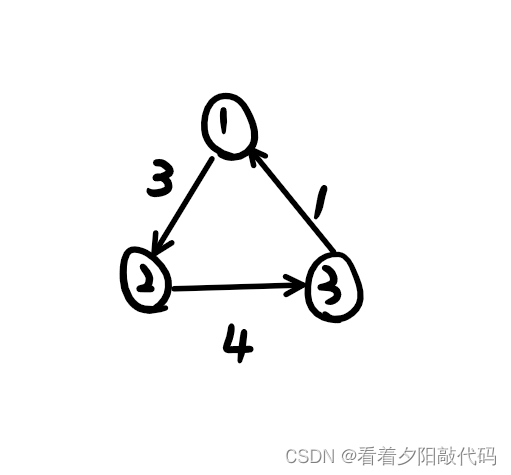
在这里插入图片描述
这里拿有向图做例子，在上图中不难发现，从①号节点走到②号节点的边权是3，从②号节点走到③号节点的边权是4…这里边权的作用就是在某些题中需求从某个节点走到某个节点所需的边权总和是多少。
图还分为稠密图和稀疏图，稀疏图就是其边的数量完全小于完全图，稠密图的边数则接近完全图。
讲完了图，下文就给大家逐个介绍一下前向星、邻接矩阵和邻接表存图的原理以及代码实现。

二、链式前向星

链式前向星的本质就是一个链表，但是其还多了一个head数组来记录头结点，利用链表可以根据一个节点去访问另一个节点的特性来进行存图操作。假设其有n个点，m条边。则其空间效率和空间效率均为O（m），适合存储稠密图。下面用代码来解释原理；

struct EDGE{
	int v,w,next;
	//v变量记录的是当前点到达那一条边。
	//w变量记录的是走过当前这条边所需的"代价"即权值
	//next变量记录的是以某一个定点为起点，读的上一条边的编号。
	//这三个变量的意义一定要搞明白，不搞明白这个，前向星的写法死记硬背也不一定行。
}e[N<<1];
int head[N],tot=1;
void add(int u,int v,int w)
{
	e[tot].v=v;
	e[tot].w=w;
	e[tot].next=head[u];
	head[u]=tot++;
}

假设这里有一个图：
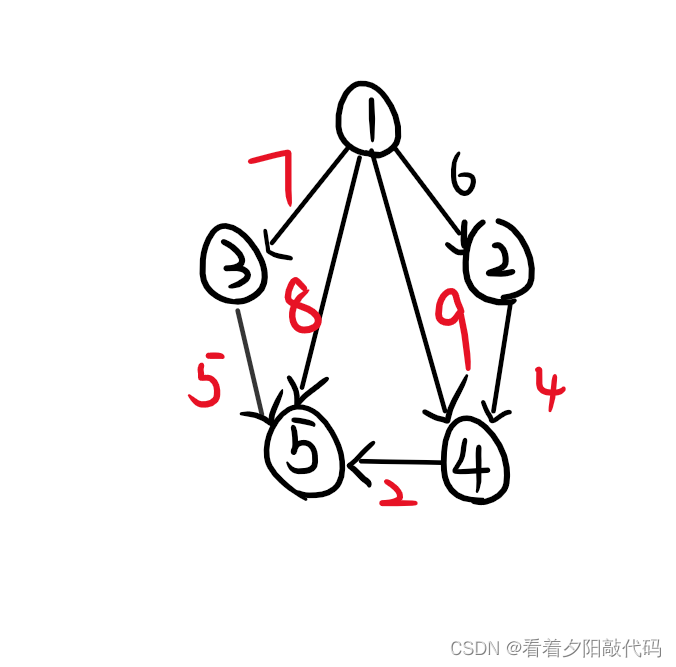
在这里插入图片描述
这是一个有向带权图，所以其各边之间的输入应为：

对应成结构体数组里的v，w，next三种变量就应该是：

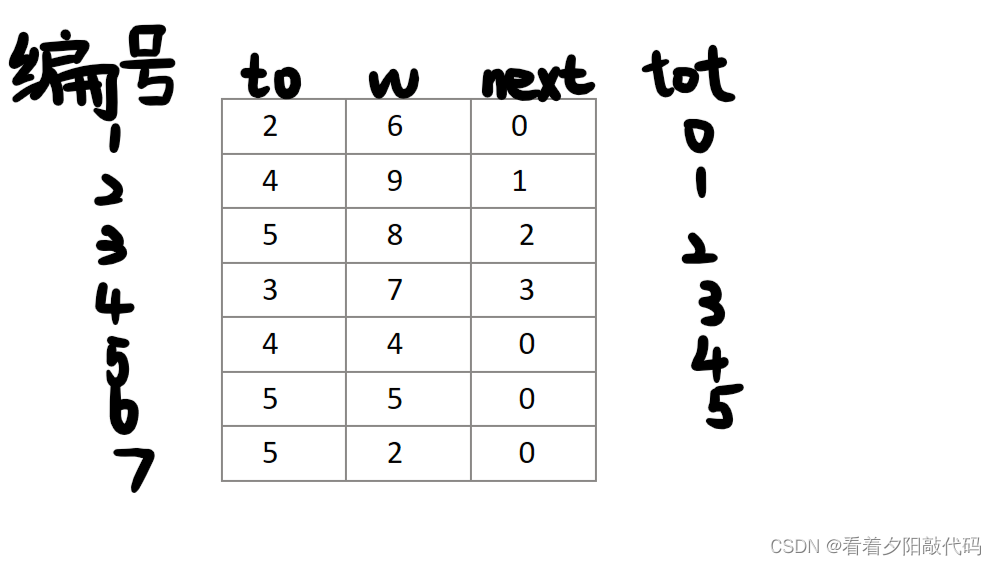
不难看出，这里tot记录的，就是上一行的编号，也就是说，我可以通过tot找到上一行的编号，从而找出先前一次存图的to，w，next；
那么head数组又是干啥的呢？让我们再画个图；
在这里插入图片描述

通过此图可知，head数组实则就是记录的以第i个编号的点为起点，我读进去的最后一条边的编号。
对于不明白者，博主在举一个例子根据代码和图来进行讲解。
可以说，head数组就是链式前向星的核心思路

假设我们要找起点为1，终点为4，边权是9的这条边。
因为起点是1，所以我们找到head[1]里面存的值是4，说明我们以1为起点读进去的最后一条边的编号为4。
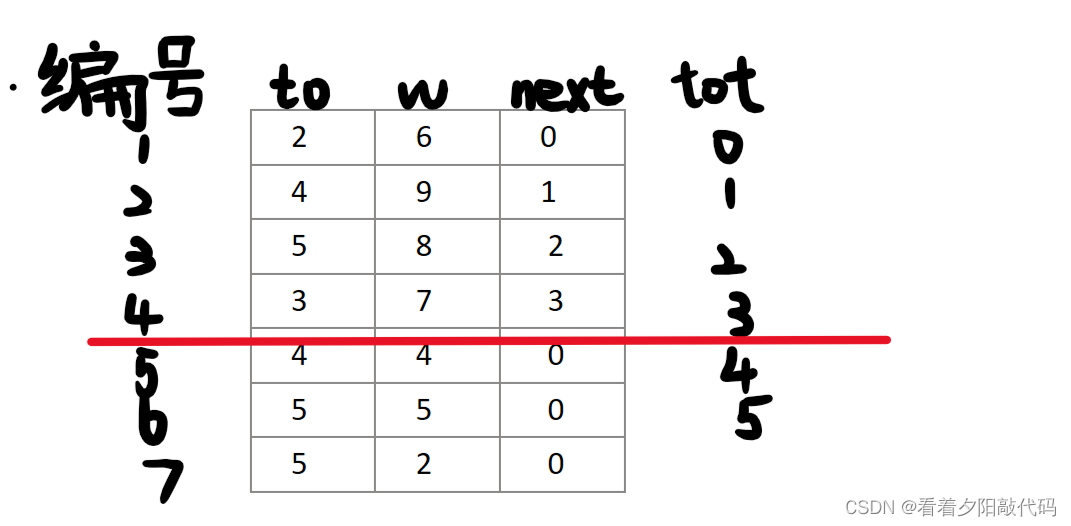
在这里插入图片描述
根据编号，我们找到上图横线的那组数据，至此，head数组的作用就发挥完了，接下来该next变量上场了。
由上图红线那一行的next变量值为3，说明上一条以1为起点的边编号是3，所以我们找到编号为3的那一行，由于不是我们要找的东西，所以我们再看编号为3的那一行的next是2，所以我们访问编号为2的那一行，结果发现，正是我们要找的那一条边，随即结束查找。
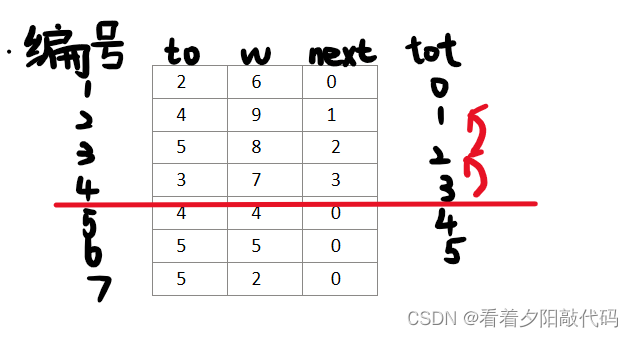
在这里插入图片描述
所以，我们由编号为3的那一条边找到编号为2的那一条边在找到结果那条边，正如上图所以，不断的搜寻不正是如一条链式的嘛，遂此存图方式叫做链式前向星。
原理看明白，接下来我会把代码的每一步根据上文所讲的图例及原理一一拆分讲解。

代码讲解：

我们将其分成两部分，一部分是结构体数组，另一部分是建边add操作。

struct EDGE{
	int v,w,next;
}e[N<<1];

结构体数组里存储的’v,w,next’分别是指向的那条边，边权和以某一个定点为起点，读的上一条边的编号。

void add(int u,int v,int w)
{
	e[tot++].v=v;//将指向的边存进去。这里注意一个点，此时是新的一条边，cnt要++；
	e[tot].w=w;//将当前的边的边权存进去
	//下面两步是最为核心的两步。
	e[tot].next=head[u];
	//我们说了，next数组存的是以某个定点为起点，读的上一条边的编号。head数组里记录的是以某个点为起点，
	//我读进去的最后一条边的编号。想一下，此时的e[tot]的这条边还没有加进去，所以此时的e[tot]的数组的
	//上一条边的编号就是我head数组存的最后一条边的编号。所以我得e[tot].next=head[u]就行啦！
	head[u]=tot;
	//此时我已经读进去了新的一条边，那此时head最后指向的是不是就是当前的边？就是此时的cnt呀，我直接赋
	//值给head[u]就行
}

呼~这就是链式前向星的的思路+代码，博主自认为讲的算是比较详细了，在写的同时也捋了一自己的思路，遂采用了最笨拙的方法。接下来给大家讲解邻接矩阵！

三、邻接矩阵

矩阵矩阵，一听这名字大家就大概能猜到这是一个二维数组（这里我要提一下，谁以为是一维数组就直接不用学了，~~你脑子太笨。。。就比如我。。。~~）
扯远了，拉回~但是这不是简简单单二维数组，在无边权的时候，数组里存储的数字’1’、‘0’，关于为啥要存着两个数呢，待会讲解，那对于有边权的图，我们数组里存储的就是边权啦。
不同于链式前向星，邻接矩阵要考虑有向图，无向图，带权图…但是其思路又要比前向星略微简单一些，两者都是存储稠密图。
我们先从有向图和无向图的角度考虑 (1) 有向图：
对于有向图来说，我从第i个点走到第j个点和从第j个点走到第i个点完全是两条不同的道路，如果不提前加进图中，不提前声明的情况下是无法走的，也可以理解成e[i][j]!=e[j][i];
(2) 无向图：
无向图则和有向图截然不同，如果我说从i到j有一条边可以走，那么我从i走到j和从j走到i都是可行的，可以理解成e[i][j]==e[j][i];
说完了有向&无向图，就到了带权与不带权的问题了，再说这个之前，我们先说一下究竟是怎么用二维数组来存储边权或者是之前提到的’0’ '1’呢？
众所周知，二维数组的写法是a[i][j]的，那我们假设从第2条边到第3条边有一个边权为4的边，那我们就可以在
e[2][3]中存一个4的值，如果我们想查看他是从哪条边指向哪条边的，是不是直接用双重for循环看一下他的i和j值就可以啦。就类似下图。

#include<iostream>
using namespace std;
int main()
{
	int m;
	int u,v,w;
	int e[10][10];
	for(int i=0;i<m;i++)
	{
		cin>>u>>v>>w;
		e[u][v]=w;
	}
	return 0;
}

在上面的代码里我们可以看见，我们的两个点是找到其边权的基础，如果题目中想查询2-3的边权，直接输出
e[2][3]就可以。当然，这只是有向带权图的代码，无向带权图只需在e[u][v]=w的后面再反向建一次边就可以了。
说完了带权图，那么不带权图该怎么写呢？
我们的思路是如果从i-j这个点有一条边，那么我们e[i][j]的值就赋为1，输入完一遍以后，我们再遍历一遍这个e数组，里面凡是不为1这个值的点就说明从没有从i-j的这一条边，所以将这些中间没边的值都赋为0。
因为这里没有代码，所以i和j说了多次，不明白的同学可以看下面的代码解释.

#include<iostream>
using namespace std;
const int N=10005;
int e[N][N];
int main()
{
	int m;//m条边
	for(int i=0;i<m;i++)
	{
		int u,v;//说明从u-v有一条边
		e[u][v]=1;//其值赋为1
	}
	for(int i=1;i<=m;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(e[i][j]!=1) e[i][j]=0;//！=1说明之前没有输入过，说明i-j没有边，赋为0；
		}
	}
	return 0;
}