0. 简介
在没有预先计算相机姿态的情况下训练神经辐射场(NeRF)是具有挑战性的。最近在这个方向上的进展表明,在前向场景中可以联合优化NeRF和相机姿态。然而,这些方法在剧烈相机运动时仍然面临困难。我们通过引入无畸变单目深度先验来解决这个具有挑战性的问题。这些先验是通过在训练期间校正比例和平移参数生成的,从而能够约束连续帧之间的相对姿态。这种约束是通过我们提出的新型损失函数实现的。对真实世界室内和室外场景的实验表明,我们的方法可以处理具有挑战性的相机轨迹,并在新视角渲染质量和姿态估计精度方面优于现有方法。本文《NoPe-NeRF: Optimising Neural Radiance Field with No Pose Prior》的项目页面是https://nope-nerf.active.vision。
1. 主要贡献
综上所述,我们提出了一种方法来联合优化摄像机的姿势和来自具有大量摄像机运动的图像序列的NeRF。我们的系统是由三个方面的贡献促成的。
-
我们提出了一种新的方法,通过明确地模拟比例和位移失真,将单深度整合到无姿势的NeRF训练中。
-
我们通过使用未扭曲的单深度地图的帧间损失,为摄像机-NeRF联合优化提供相对位置。
-
我们通过一个基于深度的表面渲染损失来进一步规范我们的相对姿势估计。
2. 详细内容
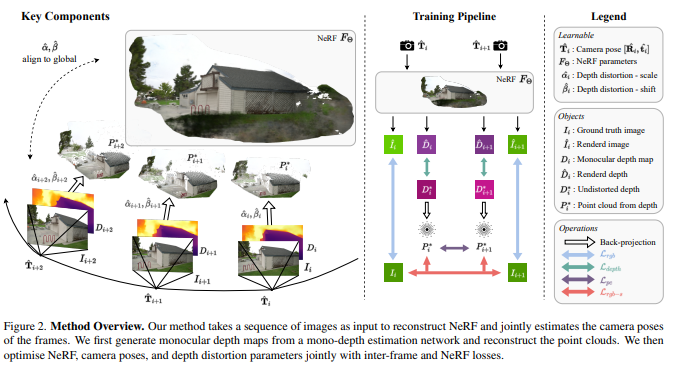
文中解决了在无姿态NeRF训练中处理大型相机运动的挑战。考虑到给定一系列图像,相机内参和它们的单目深度估计,我们的方法同时恢复相机姿态和优化NeRF。我们假设相机内参在图像元块中可用,并运行一个现成的单目深度网络DPT[7]来获取单目深度估计。在不重复单目深度的好处的情况下,我们将围绕单目深度的有效集成到无posed-NeRF训练中展开。
训练是NeRF、相机姿态和每个单目深度地图的畸变参数的联合优化。通过最小化单目深度地图与从NeRF渲染的深度图之间的差异来监督畸变参数,这些深度图是多视角一致的。反过来,无畸变深度地图有效地调解了形状-辐射(shape-radiance)的歧义,从而简化了NeRF和相机姿态的训练。
具体来说,无畸变深度地图提供了两个约束条件。我们通过在无畸变深度地图中反投影出的两个点云之间的基于Chamfer距离的对应来提供相邻图像之间的相对姿态,从而约束全局姿态估计。此外,我们通过将无畸变深度视为表面,使用基于表面的光度一致性来规范相对姿态估计。
3. NeRF与Pose
3.1 NeRF
Neural Radiance Field(NeRF)[24] 将场景表示为一个映射函数
F
Θ
:
(
x
,
d
)
→
(
c
,
σ
)
F_Θ:(x,d)→(c,σ)
FΘ:(x,d)→(c,σ),其中
x
∈
R
3
x ∈ \mathbb{R}^3
x∈R3 为 3D位置,
d
∈
R
3
d ∈ \mathbb{R}^3
d∈R3 为视角方向,
c
∈
R
3
c ∈ \mathbb{R}^3
c∈R3为辐射颜色,
σ
σ
σ 为体密度值。该映射通常是由参数化的神经网络
F
Θ
F_Θ
FΘ 实现的。给定
N
N
N 张图像
I
=
{
I
i
∣
i
=
0...
N
−
1
}
I = \{I_i | i = 0 . . . N − 1\}
I={Ii∣i=0...N−1} 及其相机姿态
Π
=
{
π
i
∣
i
=
0...
N
−
1
}
Π = \{π_i | i = 0 . . . N − 1\}
Π={πi∣i=0...N−1},可以通过最小化合成图像
I
^
\hat{I}
I^ 与捕获图像
I
I
I 之间的光度误差
L
r
g
b
=
∑
i
N
∥
I
i
−
h
a
t
I
i
∥
2
2
L_{rgb} = \sum^ N_i \| I_i − hat{I}_i\|^2_2
Lrgb=∑iN∥Ii−hatIi∥22 来优化 NeRF。
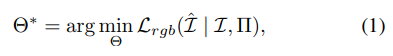
在这里,
I
^
i
\hat{I}_i
I^i是通过聚合相机射线
r
(
h
)
=
o
+
h
d
r(h) = o + hd
r(h)=o+hd上的辐射颜色在近界和远界
h
n
h_n
hn和
h
f
h_f
hf之间渲染的。更具体地说,我们使用体积渲染函数来合成
I
^
i
\hat{I}_i
I^i。
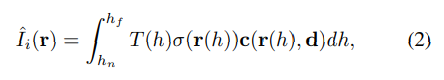
其中,
T
(
h
)
=
e
x
p
(
−
∫
h
n
h
σ
(
r
(
s
)
)
d
s
)
T(h) = exp(−\int^h_{h_n} σ(r(s))ds)
T(h)=exp(−∫hnhσ(r(s))ds) 是沿着一条射线累积的透射率。更多细节请参见[24]。
3.2 联合优化姿态和 NeRF
之前的研究 [12、18、45] 表明,可以通过在 Eq. (2) 中使用相同的体积渲染过程,在最小化上述光度误差
L
r
g
b
L_{rgb}
Lrgb 的同时估计相机参数和 NeRF。
关键在于将相机光线投射的条件设置为可变的相机参数
Π
Π
Π,因为相机光线
r
r
r 是相机姿态的函数。数学上,这种联合优化可以表示为:
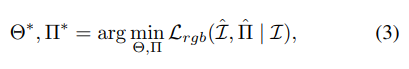
其中,符号
Π
^
\hat{\Pi}
Π^表示在优化过程中更新的相机参数。请注意,公式(1)和公式(3)之间的唯一区别在于公式(3)将相机参数视为变量。
一般来说,相机参数
Π
\Pi
Π包括相机内参、姿态和镜头畸变。本文只考虑估计相机姿态,例如,第
i
i
i帧图像的相机姿态是一个变换
T
i
=
[
R
i
∣
t
i
]
T_i=[R_i|t_i]
Ti=[Ri∣ti],其中
R
i
∈
S
O
(
3
)
R_i\in SO(3)
Ri∈SO(3)表示旋转,
t
i
∈
R
3
t_i\in \mathbb{R}^3
ti∈R3表示平移。
3.3. 单目深度的校正
使用现成的单目深度网络(如DPT [28]),我们从输入图像生成单目深度序列 D = D i ∣ i = 0... N − 1 D = {D_i | i = 0 . . . N-1} D=Di∣i=0...N−1。不出所料,单目深度图并不是多视角一致的,因此我们的目标是恢复一系列多视角一致的深度图,这些深度图进一步在我们的相对位姿损失项中得到利用。
具体而言,我们为每个单目深度图考虑两个线性变换参数,从而得到所有帧的变换参数序列
Ψ
=
(
α
i
,
β
i
)
∣
i
=
0...
N
−
1
Ψ = {(α_i,β_i) | i = 0 . . . N-1}
Ψ=(αi,βi)∣i=0...N−1,其中
α
i
α_i
αi和
β
i
β_i
βi分别表示比例因子和偏移量。在NeRF的多视角一致性约束下,我们的目标是恢复
D
i
D_i
Di的多视角一致深度图
D
i
∗
D^∗_i
Di∗:
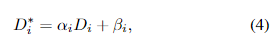
通过联合优化
α
i
α_i
αi和
β
i
β_i
βi以及NeRF,来实现这种联合优化,主要是通过在未畸变的深度图
D
i
∗
D^∗_i
Di∗和通过NeRF渲染的深度图
D
^
i
\hat{D}_i
D^i之间强制实现一致性来实现的。这种一致性通过深度损失来实现:
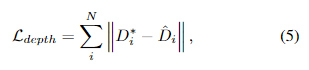
其中
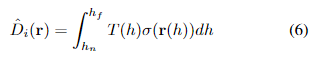
式(5)对NeRF和单目深度图都有好处。一方面,单目深度图为NeRF训练提供了强的几何先验,降低了形状-辐射度模糊性。另一方面,NeRF提供了多视角一致性,因此我们可以恢复一组多视角一致的深度图用于相对姿态估计。