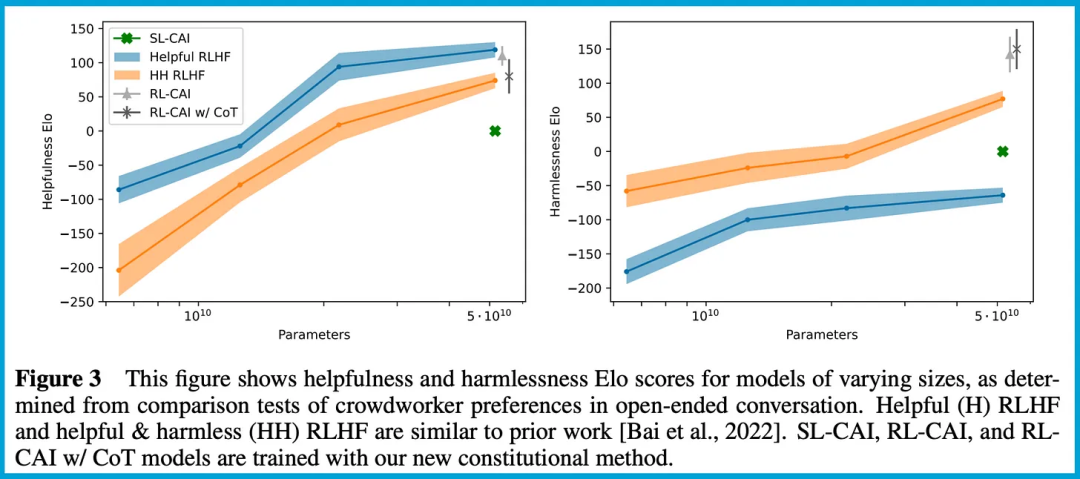
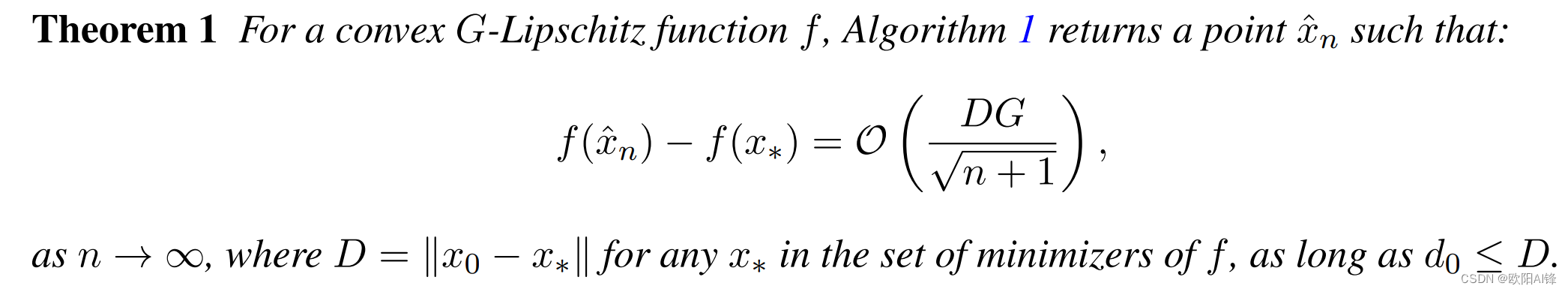考虑无约束凸Lipshcitz优化问题:
min
x
∈
R
n
f
(
x
)
.
\min_{x\in\mathbb{R}^{n}}f(x).
x∈Rnminf(x).
最常用的优化方法是子梯度下降(Subgradient descent):
x
k
+
1
=
x
k
−
γ
k
g
k
,
x_{k+1}=x_{k}-\gamma_{k}g_{k},
xk+1=xk−γkgk,
其中
g
k
∈
∂
f
(
x
k
)
g_{k}\in\partial f(x_{k})
gk∈∂f(xk).
最后的最优解为:
x
^
n
=
1
n
+
1
∑
k
=
0
n
x
k
\hat{x}_{n}=\frac{1}{n+1}\sum_{k=0}^{n} x_{k}
x^n=n+11k=0∑nxk.
学习率 γ k \gamma_{k} γk的设置一般需要关于解的距离的知识。
例如1: 设置学习率
γ
k
=
D
G
n
\gamma_{k}=\frac{D}{G\sqrt{n}}
γk=GnD,
则
f
(
x
^
n
)
−
f
∗
=
O
(
D
G
n
)
.
f(\hat{x}_{n})-f_{*}=\mathcal{O}(\frac{DG}{\sqrt{n}}).
f(x^n)−f∗=O(nDG).
这是worst-case optimal.
例如2: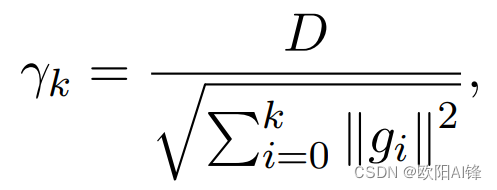
这篇论文里的方法: