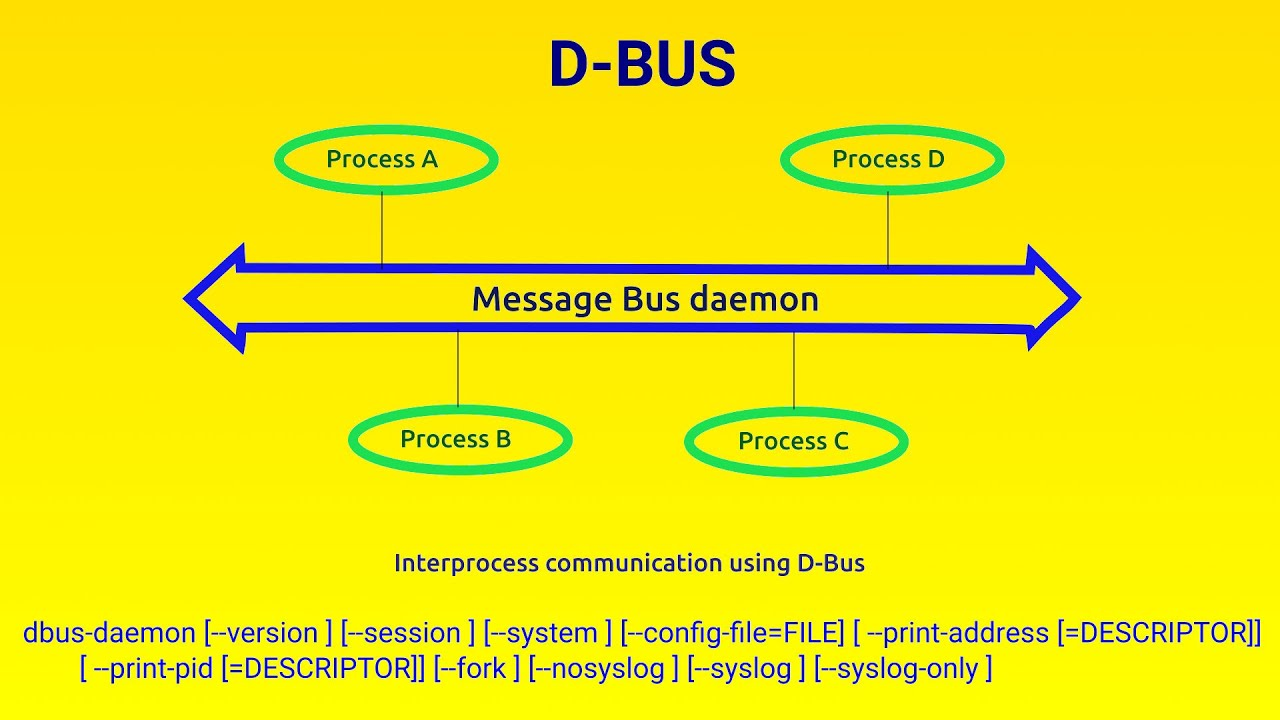
1.强化学习和深度学习的区别

强化学习和深度学习的区别：在深度学习中，像分类问题，模型做出决策之后，我们会有一个标签，告诉模型你做的对不对，是否需要改进，再决定是否更新网络。但强化学习，并不是一个监督学习，没有标签告诉模型你做的是否正确，只是说，你每走一步我告诉你你得多少分，最后通过·总分来反应一系列决策的好坏。

从应用上看：假设输入为一个老虎，深度学习只能告诉你，这是个老虎，你可以选择跑或不跑（分类），强化学习可以告诉你怎么跑（往哪一个方向，每一步该怎么走最优）。

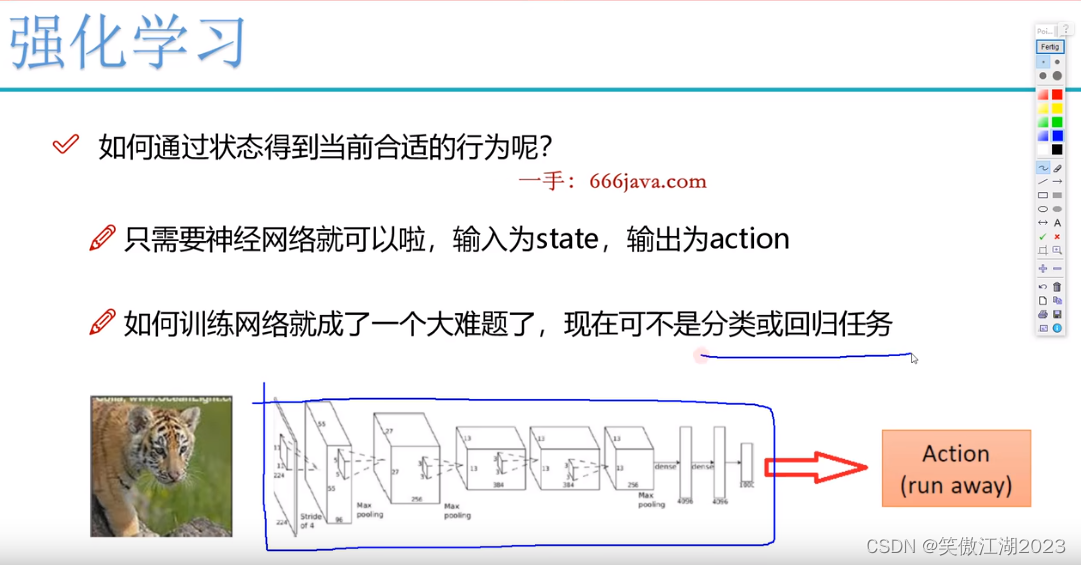
从下图进一步理解强化学习和深度学习的区别：下图游戏的目的是让小飞船平稳落地，假设我们用深度学习解决这个问题，我们发现将图像输入神经网络后，模型要输出左移还是右移的决策，这是一个二分类问题，但问题这个交互式任务，是没有标签的，在输出左移还是右移的决策之后，模型不知道和谁对比，证明左移对还是右移对。

2. 强化学习思路

强化学习思路：以上图小飞船为例，将小飞船状态state1作为输入，进入模型，得到action1（左移或右移）和这一步的R1(奖励或者惩罚)，以及state2（做完action1的下一个状态）。再将state2作为输入，得到action2（左移或右移）和这一步的R2(奖励或者惩罚)，以及state3（做完action2的下一个状态）。再将state3作为输入...。以次类推，指导满足停止条件（比方说走了1000步）。

理解强化学习模型：下图 $\pi$ 就是强化学习模型，可以参照前馈网络理解，就是网络的另一种表达方式或者说结构，R(奖励)是为了得到最优的模型 $\pi$ 。表示每一次训练周期所记录的数据。

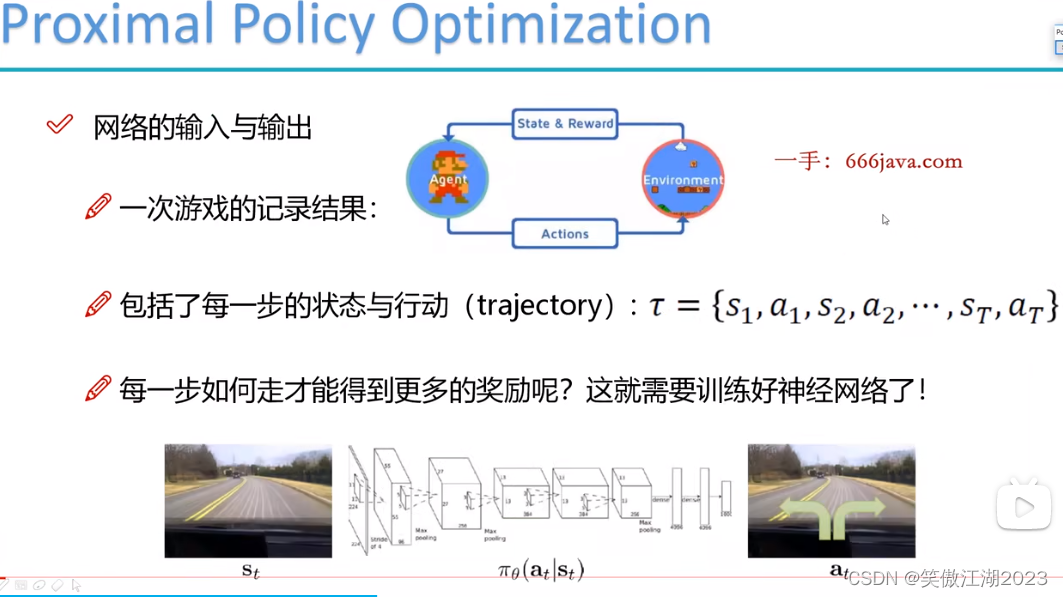
从游戏中理解一下模型中的数据：下图第一个p表示在状态为st时，有动作at得到下一个状态st+1，第二个p表示有状态st时得到下一个at的概率，而奖励R需要去设计，在模型中我们需要的数据s不需要我们设计，是交互后自然产生的，a是我们需要设计的，但设计之后a是固定的选择，不需要变化，但第二个p也就是选择哪一个动作的概率需要我们决定，这里需要一个概率转移函数，最后设计什么样的规则怎么给奖励的选择也是多样的，这里需要一个奖励函数。最后理解一下游戏记录下右侧的函数，意思是输入为s1时，每一个t所对应的动作，及这个动作所带来的对应的st+1，

理解强化学习的目标函数：在强化学习中目标函数为奖励最大值的期望，θ为需要更新的权重，为什么不直接用最大值，而用最大值的期望呢，简单理解，这样做泛化效果更好，进一步可以理解为，同样的权重但是无法保证同样的action，更无法保证同样的奖励（这就类似于，一个人让他重走一遍人生，即便所有的权重（人生大小事的选择相同）他的结果可能不一样）。进一步我们看，最下面的公式的右侧来替代奖励期望的计算，其中N代表epoch（每一个epoch代表一轮游戏），i=1-epoch，t是一个epoch里面每一个动作，r代表奖励。这个公式意思是将所有训练数据动作奖励叠加求平均，来近似奖励期望。

最后我们得到强化学习梯度计算公式：将所有训练数据带入即可更新θ。

3.baseline

在设置奖励时会发现，有些情况下无法设置惩罚，所以采用了baseline概念，就是对所有奖励求平均值，再用所有奖励减去平局值，负的为惩罚，正的为奖励。

4.PPO

4.1on-policy和off-policy简单理解

简单理解为，像小飞船落地，训练一千次，on-policy用这一千次的数据更新一次θ，而off-policy可以充分利用这一千次数据，进行多次更新。PPO算法就是基于off-policy。

怎么找打工的：简单理解，当前为θ2，打工的就是θ1，当前为θ10打工的就是θ9，因为想要的打工的是和自己最相近的，要满足两者之差小于 $\varepsilon$ ，所以认为前一个和自己最像，再用前一个的θ得到的数据，训练当前θ，就是说用θ1的训练数据训练θ2，θ2保存在θ中，再用θ2的训练数据训练θ3，再将θ3替代原θ2保存在θ中，一直跌倒到最后。

PPO2版本：如下图所示，限制条件做了改变，分子为当前θ，分母为打工θ。

4.2actotcritic

actor：当一个状态进来时确定选什么动作。分类任务，用神经网络解决。

critic：对actor选择的动作，评价好坏，输出的是一个value（值）。回归任务，用神经网络解决，全连接即可，不是卷积，上同。

进一步理解critic的作用：看下图b之前是作为奖励均值使用了，这里用critic的value替代，可以这样理解，当critic对actor选择的动作不满意时给他一个不好的评价，这个动作相对应的R-value可能会得到负值。

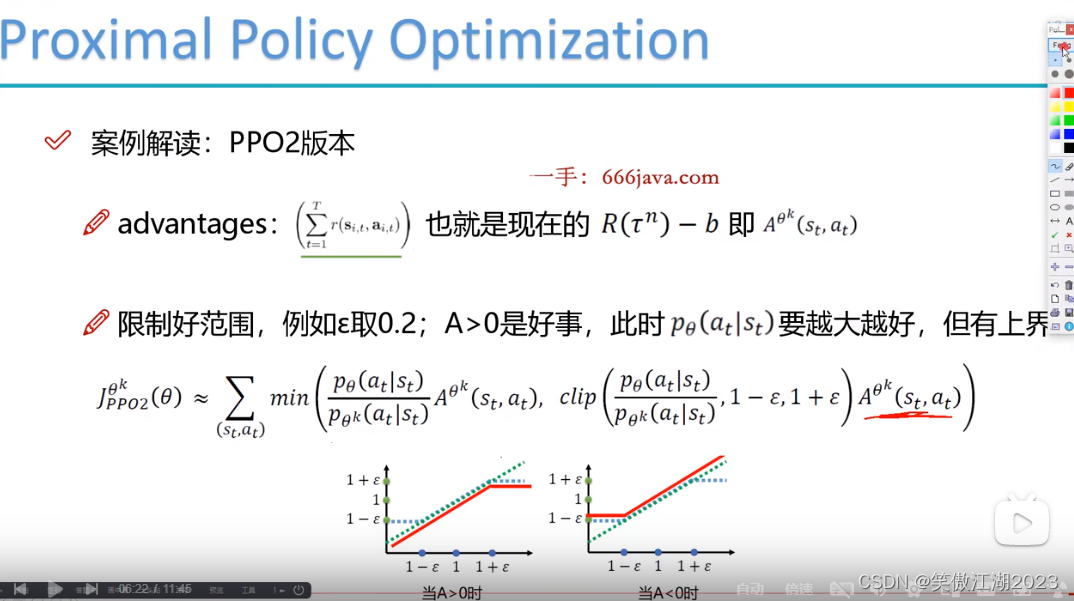
PPO2版本：R-b用A替代表示。下式求解时分两种情况，第一种A大于0时，希望分子越来越大，第二种A小于0时，希望分子越来越小。

5.DQN（回归问题）

4.1公式

yi中r表示当前状态下，该动作的奖励，加上下一个状态下最好的动作（这半句需进一步理解）。Q可以理解为一个神经网络函数，输入是s和a。

蓝框的Q用神经网络表示，得到估计值，红框是真实值，可以理解为标签值，那么这就变成了回归任务，目的就是学习Q中的w和b。进一步得到目标函数。注意到max的Q也是一个网络。

4.2Q表

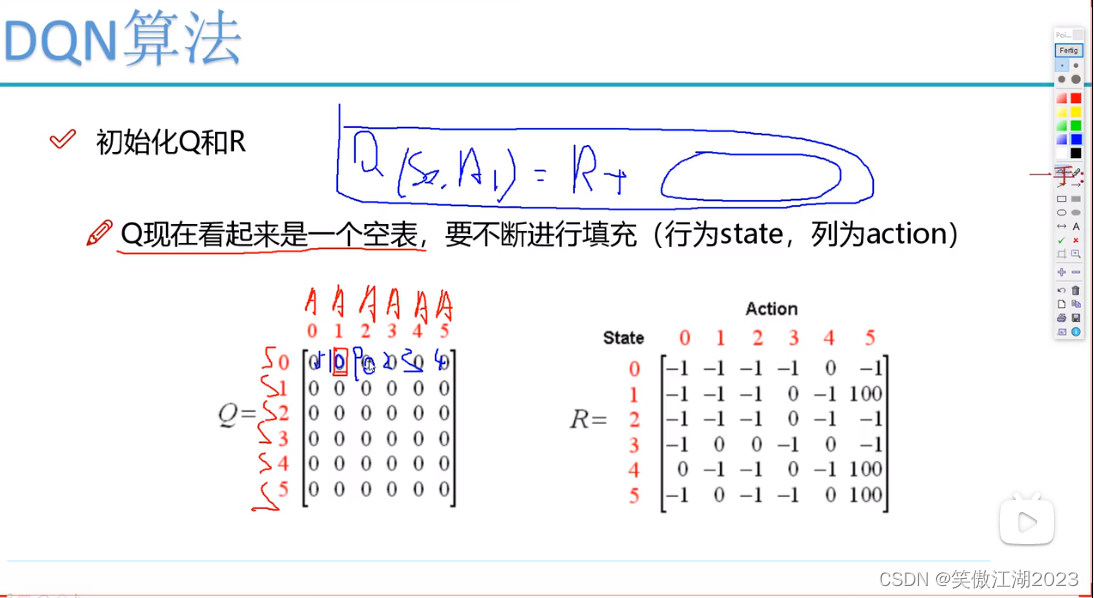
假设下列是一个已经学习过的Q表，当处在状态s0时，看相应的几个A(a)，找到最大值，对应A(a)2，作为选择动作，然后进入s1状态，继续往下。注意Q和R不同。

蓝色框对应上面一手下面的公式，<-应该是=。注意这个R是设计好的奖励规则。

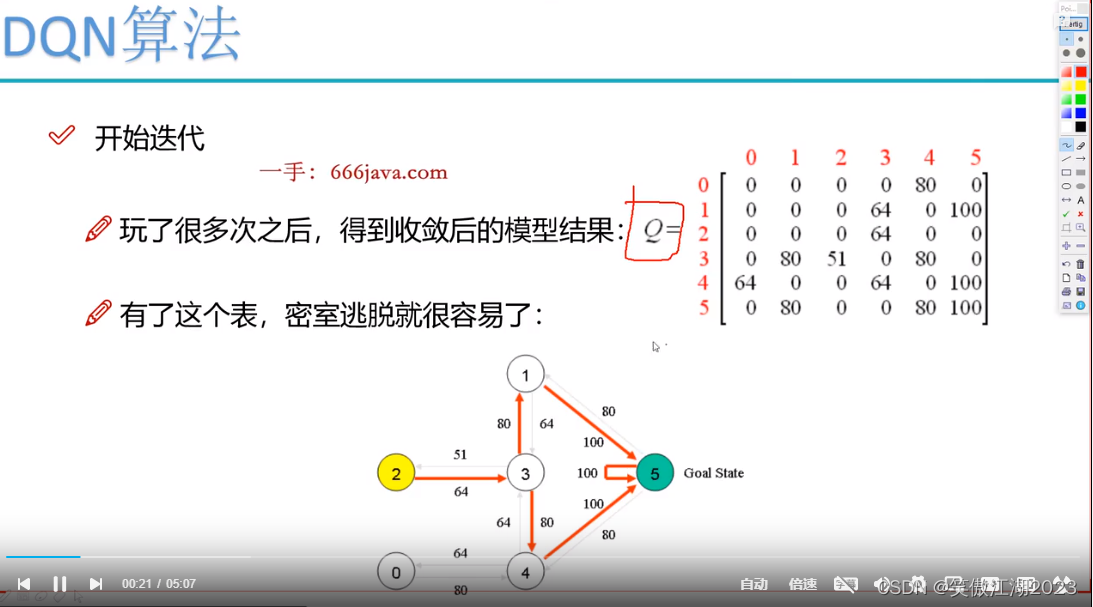
开始迭代：令上图Q全为0,R不变开始迭代，如下图所示，假设初始为s1，此时Q为0，按照R应该选择R(1,5)，此时Q(1,5)=R(1,5)+0.8*Max[Q(5,1),Q(5,4),Q(5,5)]=100+0.8*0=100。注意到[Q(5,1),Q(5,4),Q(5,5)]中选最大值，那么为什么选他们，因为在R中1，4，5是可以走的选项。那么此时Q表中就有了第一个值，然后开始第二次更新，从s3开始，如下图所示，得到另一个Q值，以此类推，进行训练。最终得到图（2.2）的Q表，图中的导线图上的Q值可以理解为神经网络的权重。在实际中，需要穷举得到可用的Q表，但不现实，所以用神经网络替代Q表的效果。