参考代码
结合自己的理解,添加注释。
代码
- 导入相关的库
import numpy as np
import pandas as pd
import matplotlib
from matplotlib import pyplot as plt
from sklearn import linear_model
- 导入数据,进行数据处理和特征工程
# 1.数据处理,特征工程
data_path = 'watermelon3_0_Ch.csv'
data = pd.read_csv(data_path).values
# 取所有行的第10列(标签列)进行判断
is_good = data[:,9] == '是'
is_bad = data[:,9] == '否'
# 按照数据集3.0α,强制转换数据类型
X = data[:,7:9].astype(float)
y = data[:,9]
y[y=='是'] = 1
y[y=='否'] = 0
y = y.astype(int)
- 定义若干需要使用的函数
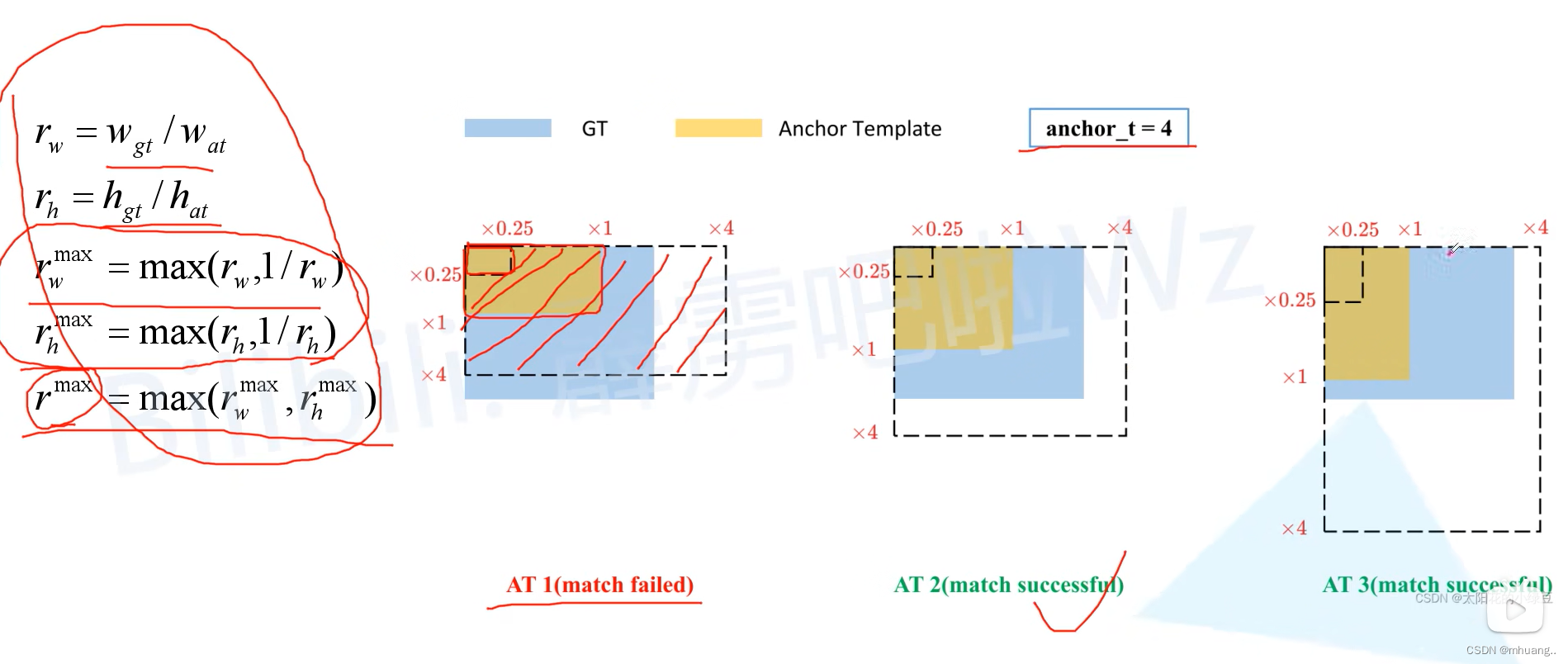
y = 1 1 + e − x y= \frac{1}{1+e^{-x}} y=1+e−x1
def sigmoid(x):
"""
构造对数几率函数,它是一种sigmoid函数
"""
s = 1/(1+np.exp(-x))
return s
ℓ ( β ) = ∑ i = 1 m ( − y i β T x ^ i + l n ( 1 + e β T x ^ i ) ) \ell(\beta) = \sum_{i=1}^{m}(-y_{i}\beta^{T} \hat{x}_{i} + ln(1+e^{\beta^{T} \hat{x}_{i}})) ℓ(β)=i=1∑m(−yiβTx^i+ln(1+eβTx^i))
def J_cost(X,y,beta):
"""
:param X: sample array, shape(n_samples, n_features)
:param y: array-like, shape (n_samples,)
:param beta: the beta in formula 3.27 , shape(n_features + 1, ) or (n_features + 1, 1)
:return: the result of formula 3.27
"""
# 构造x_hat,np.c_ 用于连接两个矩阵,规模是(X.row行,X.column+1列)
X_hat = np.c_[X, np.ones((X.shape[0],1))]
# β和y均reshape为1列,规模是(X.column+1行,1列)
beta = beta.reshape(-1,1)
y = y.reshape(-1,1)
# 计算最大化似然函数的相反数
L_beta = -y * np.dot(X_hat,beta) + np.log(1+np.exp(np.dot(X_hat,beta)))
# 返回式3.27的结果
return L_beta.sum()
β = ( w ; b ) \beta = (w; b) β=(w;b)
def initialize_beta(column):
"""
初始化β,对应式3.26的假设,规模是(X.column+1行,1列),x_hat规模是(17行,X.column+1列)
"""
# numpy.random.randn(d0,d1,…,dn)
# randn函数返回一个或一组样本,具有标准正态分布。标准正态分布又称为u分布,是以0为均值、以1为标准差的正态分布,记为N(0,1)
# dn表格每个维度
# 返回值为指定维度的array
beta = np.random.randn(column+1,1)*0.5+1
return beta
∂ ℓ ( β ) ∂ β = − ∑ i = 1 m x ^ i ( y i − p 1 ( x ^ i ; β ) ) \frac{\partial \ell(\beta)}{\partial \beta} = -\sum_{i=1}^{m}\hat{x}_{i}(y_{i}-p_{1}(\hat{x}_{i};\beta)) ∂β∂ℓ(β)=−i=1∑mx^i(yi−p1(x^i;β))
def gradient(X,y,beta):
"""
compute the first derivative of J(i.e. formula 3.27) with respect to beta i.e. formula 3.30
计算式3.27的一阶导数
----------------------------------------------------
:param X: sample array, shape(n_samples, n_features)
:param y: array-like, shape (n_samples,)
:param beta: the beta in formula 3.27 , shape(n_features + 1, ) or (n_features + 1, 1)
:return:
"""
# 构造x_hat,np.c_ 用于连接两个矩阵,规模是(X.row行,X.column+1列)
X_hat = np.c_[X, np.ones((X.shape[0],1))]
# β和y均reshape为1列,规模是(X.column+1行,1列)
beta = beta.reshape(-1,1)
y = y.reshape(-1,1)
# 计算p1(X_hat,beta)
p1 = sigmoid(np.dot(X_hat,beta))
gra = (-X_hat*(y-p1)).sum(0)
return gra.reshape(-1,1)
∂ 2 ℓ ( β ) ∂ β ∂ β T = ∑ i = 1 m x ^ i x ^ i T p 1 ( x ^ i ; β ) ( 1 − p 1 ( x ^ i ; β ) ) \frac{\partial^2 \ell(\beta)}{\partial \beta \partial \beta^T} = \sum_{i=1}^{m}\hat{x}_{i}\hat{x}_{i}^Tp_{1}(\hat{x}_{i};\beta)(1-p_{1}(\hat{x}_{i};\beta)) ∂β∂βT∂2ℓ(β)=i=1∑mx^ix^iTp1(x^i;β)(1−p1(x^i;β))
def hessian(X,y,beta):
'''
compute the second derivative of J(i.e. formula 3.27) with respect to beta i.e. formula 3.31
计算式3.27的二阶导数
----------------------------------
:param X: sample array, shape(n_samples, n_features)
:param y: array-like, shape (n_samples,)
:param beta: the beta in formula 3.27 , shape(n_features + 1, ) or (n_features + 1, 1)
:return:
'''
# 构造x_hat,np.c_ 用于连接两个矩阵,规模是(X.row行,X.column+1列)
X_hat = np.c_[X, np.ones((X.shape[0],1))]
# β和y均reshape为1列,规模是(X.column+1行,1列)
beta = beta.reshape(-1,1)
y = y.reshape(-1,1)
# 计算p1(X_hat,beta)
p1 = sigmoid(np.dot(X_hat,beta))
m,n=X.shape
# np.eye()返回的是一个二维2的数组(N,M),对角线的地方为1,其余的地方为0.
P = np.eye(m)*p1*(1-p1)
assert P.shape[0] == P.shape[1]
# X_hat.T是X_hat的转置
return np.dot(np.dot(X_hat.T,P),X_hat)
使用梯度下降法求解
def update_parameters_gradDesc(X,y,beta,learning_rate,num_iterations,print_cost):
"""
update parameters with gradient descent method
"""
for i in range(num_iterations):
grad = gradient(X,y,beta)
beta = beta - learning_rate*grad
# print_cost为true时,并且迭代为10的倍数时,打印本次迭代的cost
if (i%10==0)&print_cost:
print('{}th iteration, cost is {}'.format(i,J_cost(X,y,beta)))
return beta
def logistic_model(X,y,print_cost=False,method='gradDesc',learning_rate=1.2,num_iterations=1000):
"""
:param method: str 'gradDesc'or'Newton'
"""
# 得到X的规模
row,column = X.shape
# 初始化β
beta = initialize_beta(column)
if method == 'gradDesc':
return update_parameters_gradDesc(X,y,beta,learning_rate,num_iterations,print_cost)
elif method == 'Newton':
return update_parameters_newton(X,y,beta,print_cost,num_iterations)
else:
raise ValueError('Unknown solver %s' % method)
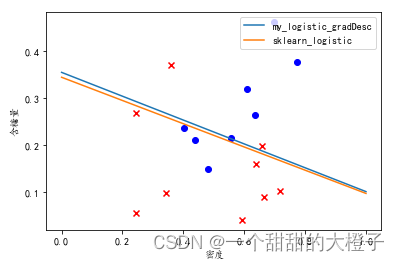
- 可视化结果
# 1.可视化数据点
# 设置字体为楷体
matplotlib.rcParams['font.sans-serif'] = ['KaiTi']
plt.scatter(data[:, 7][is_good], data[:, 8][is_good], c='b', marker='o') #c参数是颜色,marker是标记
plt.scatter(data[:, 7][is_bad], data[:, 8][is_bad], c='r', marker='x')
# 设置横轴坐标标题
plt.xlabel('密度')
plt.ylabel('含糖量')
# 2.可视化自己写的模型
# 学习得到模型
beta = logistic_model(X,y,print_cost=True,method='gradDesc',learning_rate=0.3, num_iterations=1000)
# 得到模型参数及偏置(截距)
w1, w2, intercept = beta
x1 = np.linspace(0, 1)
y1 = -(w1 * x1 + intercept) / w2
ax1, = plt.plot(x1, y1, label=r'my_logistic_gradDesc')
# 3.可视化sklearn的对率回归模型,进行对比
lr = linear_model.LogisticRegression(solver='lbfgs', C=1000) # 注意sklearn的逻辑回归中,C越大表示正则化程度越低。
lr.fit(X, y)
lr_beta = np.c_[lr.coef_, lr.intercept_]
print(J_cost(X, y, lr_beta))
# 可视化sklearn LogisticRegression 模型结果
w1_sk, w2_sk = lr.coef_[0, :]
x2 = np.linspace(0, 1)
y2 = -(w1_sk * x2 + lr.intercept_) / w2
ax2, = plt.plot(x2, y2, label=r'sklearn_logistic')
plt.legend(loc='upper right')
plt.show()
可视化结果如下: